Loss rebates
December 27, 2004
1 Introduction
The game is defined by a list of payouts u
1
, u
2
,. . . , u
`
, and a list of probabil-
ities p
1
, p
2
, . . . , p
`
,
`
P
i=1
p
i
= 1. We allow u
i
to be rational numbers, not just
integers, to include games like blackjack, n-play video poker or the banker bet
in baccarat. We assume that the casino has the advantage, so
`
P
i=1
p
i
u
i
< 0.
The player can bet any positive integer k up to his current bankroll or
the maximum bet b, whichever is smaller, and his bankroll increases by u
i
k
with probability p
i
. To cater for blackjack or poker type games, only the
player’s initial bet is limited, and we allow the player to borrow money for
splits, doubles or raises if necessary, but he has to stop if he loses and ends
up with a negative bankroll. Each game is independent of all others.
Several casinos have promotions where they give the player 10% of his
losses each month or on certain days, and VIP Casino also gives a 1% bonus
on the winnings. In this paper we investigate the value of these bonuses and
the optimal strategy for them. We assume that the bonus is withdrawable
without further wagering requirements.
2 The questions
If the player’s initial bankroll is m, his current bankroll is n, and the casino
offers a 10% rebate on losses, what strategy should the player follow to maxi-
mize his expectation and what is this expectation a
n
? What if the casino also
offers a 1% bonus on winnings?
1
n can be a rational number whose denominator is the least common mul-
tiple of the denominators of the u
i
, for example, when dealing with blackjack,
n can be a half integer, but the stake is always an integer and let us also
define a
n
= n + 0.1m for n < 0.
Define the value of the promotion to be the amount the player expects to
gain by playing optimally instead of cashing in immediately.
In games involving an element of skill, we assume that the player is play-
ing a fixed strategy, possible adjustments to playing strategy in view of the
changed expected values are not considered, strategy will only mean betting
strategy.
3 The solution
These problem can be solved by the same iterative method as the phantom
bonus problem, so the details are not repeated here. For the simple 10%
rebate the starting values need to be set to a
n,0
= 0.9n+0 .1 m for 0 ≤ n ≤ m,
and a
n,0
= n for n > m. For the VIP Casino problem, set a
n,0
= 1.01n −
0.01m for n > m. There are a priori bounds on how high the player should
aim, he should stop if his bankroll exceeds
³
m
X
u
i
<0
p
i
u
i
´.³
10
`
X
i=1
p
i
u
i
´
in the
case of the loss rebate, or
³
0.11m
X
u
i
<0
p
i
u
i
´.³
1.01
`
X
i=1
p
i
u
i
´
in the case of the
VIP Casino promotion.
4 The results
The tables in the Appendix show the results for various games. The player’s
initial bankroll was always taken to be m = 100, this way the maximum
amount of the loss rebate is 10 and the figures can be compared to those
obtained for the phantom bonus. The probabilities for blackjack were taken
from a simulation by Michael Shackleford, the “Wizard of Odds”, available
on the web at http://www.wizardofodds.com/games/blackjack/bjapx4.html.
The first table for each game is for the 10% loss rebate, the second table
for the VIP Casino promotion. In each table the first column shows the max-
imum bet, the second and third columns the smallest and largest bankrolls,
2
respectively, at which it is still in the player’s interest to play, rather than to
cash in. If the number in the second column is 1, it means that the player
should play until his bankroll exceeds the number in the third column or
go bust. The fourth column shows the value of the promotion at the initial
bankroll.
These calculations required much more computer time than for the phan-
tom bonus, the most difficult case was Cryptologic Double Bonus video poker
with 1% bonus on winnings with b = 1, this took about 16 hours on a com-
puter with a 2.2 GHz Intel Pentium processor. This is probably due to the
fractions involved. The calculations had to be done using exact arithmetic,
the standard 16 digits numerical precision was not enough, it sometimes
caused the iterations to diverge. Some calculations were done using smaller
numbers (e.g., m = b = 10 instead of m = b = 100) and then scaled up. As
a consequence, the numbers in the second and third columns are not always
exact, but they are always accurate within one maximum bet.
There are some new phenomena with the loss rebate which do not occur
with the phantom bonus. It is clearly never in the player’s interest to stop
if his bankroll does not exceed the phantom bonus. With the loss rebate, if
the house edge is too high, the player should simply not play. Such games
are the tie bet in baccarat and the coin flip with the probability of winning
0.45, these games are not included in the tables. If it is not in the player’s
interest to play at the initial bankroll, he should not play at all. Even for
other games, the strategy is not always “aim for a high target or go bust”,
but “aim for a high target or stop at a stop loss limit greater than 0”. For
example, when playing blackjack with the 10% loss rebate, the player should
stop when his losses exceed 7.5 maximum bets or when his winnings exceed
7 maximum bets, with the additional 1% bonus on profits, the limits are 8
maximum bets either way. This assumes that the initial bankroll is more
than 7.5 or 8 maximum bets. The additional 1% bonus on winnings calls for
a slightly more aggressive strategy in general.
It is interesting to note that when the stop loss limit it 0, the target
bankroll for the 10% loss rebate on 100 units is the same as for the 10 unit
phantom bonus, the calculations in the next section will explain this. This
also shows that the loss rebate requires a much less aggressive strategy.
Many observations are the same as for the phantom bonus. The value of
the promotions, and also the upper bound on the bankroll at which the player
should stop playing both increase with b, while the lower bound decreases
with b. The value of these promotions is maximal at the initial bankroll.
3
The house edge is not the primary factor in determining the value of the
promotions, a large probability of losing and a small probability of winning
a large amount is the good for the player. Among all the roulette bets,
which all have the same house edge, betting on a single number is the best.
Similarly, Jacks or Better video poker with doubling is better than without
doubling, while the house edge is the same. The line bet (6 numbers) in
roulette with house edge 2.7% is better for the player than coin flip with
probability of winning 0.495 and house edge 1%. The numbers for coin flip
with probability of winning 0.499 and house edge 0.2% are similar to those
for Jacks or Better video poker with house edge 0.46%. The best game is
Cryptologic Double Bonus video poker, which combines both a low house
edge (0.06%) and the possibility of big wins. The value of the VIP Casino
promotion for this game with large enough bets may exceed 10, of course,
this comes at the expense of extremely large variance.
The value of the loss rebate is usually less than that of the phantom bonus,
it is possible to realize about 90% of the nominal value of the phantom bonus
on most games with high enough maximum bet, while only video pokers, the
single number bet in roulette and the coin flip with the probability of winning
0.499 achieve more than 70% with the loss rebate. The extra 1% bonus on
winnings increases the value of the promotion by about 15%.
5 Details of the strategy
Let kb be the largest and k
0
b the smallest multiple of the maximum bet
at which the player should still play. They can be calculated by a similar
method as in the case of phantom bonuses.
Assume that all the payouts are integers ≥ −1. Empirical evidence
suggests that if player’s bankroll is a multiple of b, he should always bet
the maximum, b. Let u = max{u
i
|1 ≤ i ≤ `}. The numbers a
jb
(k
0
≤
j ≤ k) satisfy the recurrence relation a
jb
=
`
P
i=1
p
i
a
(j+u
i
)b
together with the
boundary conditions a
(k
0
−1)b
= 0.9(k
0
− 1)b + 0.1m and a
(k+1)b
= (k + 1)b,
a
(k+2)b
= (k + 2)b,. . . , a
(k+u)b
= (k + u)b in the case of the 10% loss re-
bate. In the case of the VIP Casino promotion, the equations have to be
changed to a
(k+1)b
= 1.01(k + 1)b − 0.01m, a
(k+2)b
= 1.01(k + 2)b − 0.01m,. . . ,
a
(k+u)b
= 1.01(k + u)b − 0.01m.
Given a pair of positive integers t
0
≤ m/b and t ≥ m/b, we can define
4
α
jb,t
0
,t
by substituting it for a
jb
in the above equations. The pair is suitable
if a
t
0
b,t
0
,t
≥ 0.9t
0
b + 0.1n and a
tb,t
0
,t
≥ tb in the case of the 10% loss rebate,
while in the case of the VIP Casino promotion, the second inequality has to
be replaced by a
tb,t
0
,t
≥ 1.01tb − 0.01m.
k
0
is the smallest possible value of t
0
and k is the largest possible value
of t in a suitable pair, they can be found by searching, but there does not
appear to be any method of finding them directly.
If k
0
= 1, meaning that the player should play until he either reaches his
goal or goes bust, the 10% loss rebate with initial bankroll 100 units and the
phantom bonus of 10 units give the same equations for k, this explains the
observation in the previous section.
If the maximum bet is large enough or there is no maximum bet and all
the payouts are integers greater than or equal to −1, then the player should
bet his whole bankroll until he either reaches the goal given in Section 3 or
goes bust.
It might be expected that the player should always bet the table limit
or his whole bankroll, and just like in the case of the phantom bonus, this
is usually correct, but not always. With the phantom bonus, the correct
strategy was always to bet either the maximum or difference between the
current bankroll and the largest multiple of the maximum bet not exceeding
it, so that if the player lost, his bankroll would be an integer multiple of
the maximum bet. There is a tendency to favor multiples of the maximum
bet with the loss rebate, too, but the bet size may be such that the player’s
bankroll will be equal to or just slightly greater than an integer multiple
of the maximum bet if he wins. For even money bets, 1/2, 1/4 or 1/8 of
the maximum bet may also be a desirable goal. The tables below show the
bankroll and optimal bet size for various games to illustrate these principles.
Roulette, even money bets, b = 100, 10% loss rebate
n 52 53 54 55 . . . 70 71 72 73 74 75
bet 48 47 46 45 . . . 30 29 28 27 26 75
For 52 ≤ n ≤ 74, the player aims to get to 100 if he wins.
Roulette, column or dozen bets, payout 2:1, b = 100, 10% loss rebate
n 21 22 23 24 . . . 33 34 35 36 37 38 39 40 41 42
bet 6 5 5 24 . . . 33 33 33 32 32 31 31 30 30 29
For 34 ≤ n ≤ 42, the player aims to get to 100 or 101 if he wins.
5

Coin flip, probability of winning 0.49, b = 100, 10% loss rebate
n 34 35 36 37 38 39 40
bet 16 15 14 13 12 39 40
Coin flip, probability of winning 0.49, b = 100, VIP Casino promotion
n 27 28 29 30 31 32 33 34
bet 23 22 21 20 19 18 17 34
In the above two cases, for 34 ≤ n ≤ 38 and for 27 ≤ n ≤ 33, respectively,
the player aims to get 50 = b/2 if he wins.
Baccarat, player bet, b = 100, VIP Casino promotion
n 9 10 11 12 13 14 15 16 17
bet 4 10 11 12 12 11 10 9 17
For 13 ≤ n ≤ 16, the player aims to get 25 = b/4 if he wins. There is a
similar example with b = 200, the optimal bet with a bankroll of 13 is 12.
The last two tables show cases where the optimal strategy cannot be
explained easily.
Roulette, split bet (2 numbers), payout 18:1, b = 50, VIP Casino promotion
n 50 51 52 53 . . . 60 61 62 63 64 65 66 67 68 69
bet 50 1 50 50 . . . 50 50 1 50 50 50 50 17 18 19
Roulette, corner bet (4 numbers), payout 9:1, b = 100, VIP Casino promotion
n 101 102 103 104 105 . . . 109 110 111 112 113
bet 100 2 3 4 100 . . . 100 2 3 100 100
6 The effects of using the wrong strategy
As the previous section shows, the optimal betting strategy is quite far from
obvious. Fortunately, the simple strategy of betting the whole bankroll or the
maximum allowed, whichever is smaller, is quite good, and in the few cases
I looked at it never caused a loss of more than 0.5% of the initial bankroll
compared to the optimal strategy.
The other element of the strategy is the correct target and stop loss limit.
Too timid a strategy will fail to realize the value of the loss rebate, while too
agressive a strategy will also cause the player to lose because of the house
edge. The correct target is often around three times the initial bankroll, if
the player choose to double or to quadraple his bankroll instead, he may give
up 0.5% of his initial bankroll, but this can mean 10–15% of the value of
the loss rebate. Too agressive a strategy is more dangerous, playing on after
6
reaching the correct target instead of cashing in can cost 5% or more of the
initial bankroll and even wipe out any expected profit from the loss rebate.
7 Appendix
Baccarat (8 decks): player bet
1 99 101 0.048141
2 98 102 0.0962819
5 93 107 0.240705
10 86 114 0.48141
20 71 128 0.962819
50 28 170 2.40705
100 12 225 4.0399
200 8 286 4.85648
500 7 371 4.85648
1 99 101 0.057868
2 97 103 0.115736
5 92 107 0.28934
10 84 115 0.57868
20 67 131 1.15736
50 22 178 2.8934
100 9 236 4.68845
200 6 303 5.58615
500 5 404 5.60089
Blackjack
1 92.5 107 0.201784
2 85 114 0.403568
5 62.5 135 1.00892
10 25 170 2.01595
20 1 235 3.54223
50 1 350 5.35131
100 1 460 6.35234
1 92 108 0.242936
2 84 116 0.485872
5 60 140 1.21468
10 20 180 2.42494
20 1 245 4.14159
50 1 370 6.11084
100 1 500 7.25468
Coin flip, probability of winning 0.48
1 100 100 0.012
2 100 100 0.024
5 99 101 0.06
10 98 102 0.12
20 96 104 0.24
50 88 111 0.6
100 81 123 1.2
1 100 100 0.0168
2 100 100 0.0336
5 99 101 0.084
10 97 102 0.168
20 94 105 0.336
50 85 114 0.84
100 76 129 1.68
7
Coin flip, probability of winning 0.49
1 100 100 0.031
2 99 101 0.062
5 96 104 0.155
10 92 108 0.31
20 83 116 0.62
50 56 141 1.55
100 34 179 3.1
1 100 100 0.0359
2 99 101 0.0718
5 96 104 0.1795
10 91 109 0.359
20 81 118 0.718
50 51 146 1.795
100 27 190 3.59
Coin flip, probability of winning 0.495
1 98 102 0.0645228
2 96 104 0.129046
5 90 110 0.322614
10 79 121 0.645228
20 57 142 1.29046
50 11 203 3.13008
100 4 270 4.73984
1 98 102 0.0790729
2 96 104 0.158146
5 88 111 0.395365
10 76 123 0.790729
20 51 146 1.58146
50 7 212 3.71214
100 3 285 5.39322
Coin flip, probability of winning 0.499
1 88 112 0.328972
2 75 124 0.657944
5 36 162 1.64486
10 1 222 3.17062
20 1 309 4.75243
50 1 478 6.4383
100 1 660 7.39252
1 86 113 0.396093
2 72 127 0.792186
5 30 168 1.98047
10 1 232 3.7247
20 1 323 5.42949
50 1 501 7.22636
100 1 692 8.23941
European roulette: straight up (single number)
1 67 121 0.823681
2 33 143 1.64736
5 1 201 3.69786
10 1 252 5.2068
20 1 295 6.15924
50 1 332 6.80058
100 1 347 7.02703
1 64 124 0.991716
2 27 149 1.98343
5 1 212 4.28873
10 1 268 5.94317
20 1 317 7.00561
50 1 358 7.7206
100 1 376 7.97297
8
European roulette: split bet (2 numbers)
1 84 110 0.400049
2 68 121 0.800097
5 20 152 2.00024
10 3 198 3.63066
20 1 249 5.14822
50 1 302 6.31848
100 1 327 6.75676
1 83 112 0.481785
2 65 124 0.96357
5 13 160 2.40893
10 1 209 4.21609
20 1 265 5.88137
50 1 324 7.187
100 1 352 7.67568
European roulette: street bet (3 numbers)
1 90 106 0.258869
2 80 113 0.517739
5 50 133 1.29435
10 9 167 2.5842
20 2 216 4.25364
50 1 277 5.85099
100 1 309 6.48649
1 89 107 0.311842
2 78 115 0.623684
5 44 138 1.55921
10 7 176 3.0839
20 1 228 4.88587
50 1 296 6.66947
100 1 332 7.37838
European roulette: corner bet (4 numbers)
1 93 104 0.188205
2 86 109 0.37641
5 64 124 0.941024
10 28 149 1.88205
20 6 192 3.491
50 2 256 5.3981
100 1 293 6.21622
1 92 105 0.226707
2 84 111 0.453414
5 60 127 1.13354
10 20 155 2.26707
20 3 203 4.06435
50 1 272 6.16801
100 1 314 7.08108
European roulette: line bet (6 numbers)
1 96 103 0.11745
2 92 106 0.234901
5 79 115 0.587252
10 57 130 1.1745
20 18 160 2.34901
50 5 221 4.53616
100 3 263 5.67568
1 96 103 0.141873
2 91 106 0.283746
5 76 117 0.709364
10 52 134 1.41873
20 15 168 2.83746
50 3 234 5.21329
100 2 282 6.48649
9
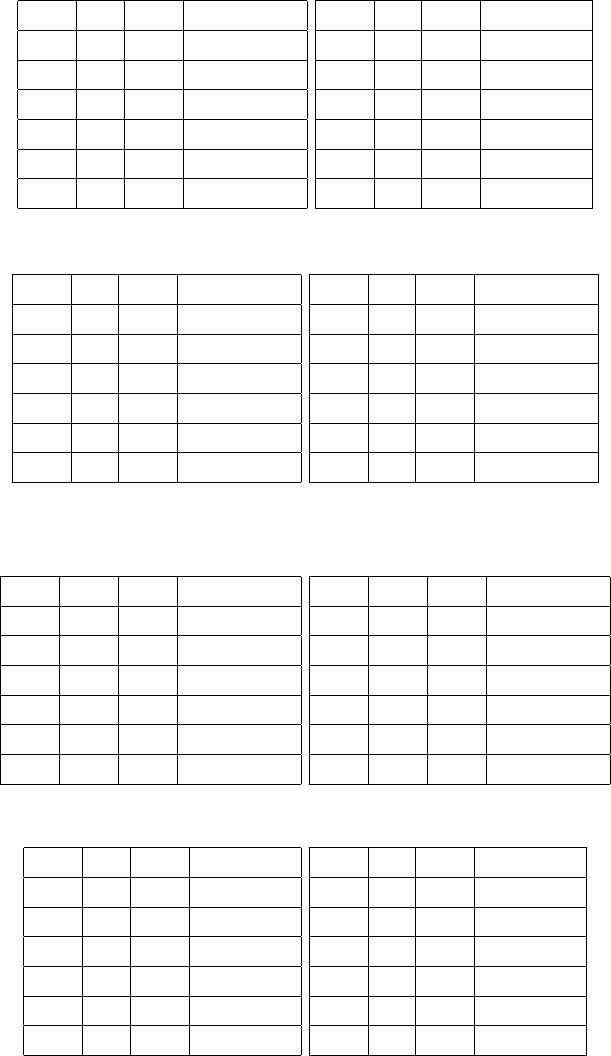
European roulette: 9 numbers
1 98 101 0.0707495
2 96 103 0.141499
5 88 108 0.353748
10 76 117 0.707495
20 52 134 1.41499
50 14 183 3.35281
100 9 227 4.86486
1 98 102 0.084644
2 95 104 0.169288
5 87 110 0.42322
10 73 120 0.84644
20 46 140 1.69288
50 12 194 3.90175
100 6 240 5.59459
European roulette: dozen or column bets (12 numbers)
1 99 101 0.0470651
2 98 102 0.0941302
5 93 105 0.235325
10 86 111 0.470651
20 71 122 0.941302
50 36 156 2.35325
100 21 200 4.05405
1 99 101 0.0571817
2 97 102 0.114363
5 92 106 0.285908
10 84 112 0.571817
20 67 125 1.14363
50 30 164 2.85908
100 16 210 4.7027
European roulette: even money bets (18 numbers),
no en prison rule or half of your stake back on 0
1 100 100 0.0243243
2 100 100 0.0486486
5 98 102 0.121622
10 96 104 0.243243
20 91 109 0.486486
50 76 123 1.21622
100 52 147 2.43243
1 100 100 0.0291892
2 99 101 0.0583784
5 97 102 0.145946
10 94 105 0.291892
20 88 111 0.583784
50 70 128 1.45946
100 48 154 2.91892
Full pay Jacks or Better video poker
1 67 121 0.725652
2 34 143 1.4513
5 1 201 3.27731
10 1 264 4.6667
20 1 344 5.81142
50 1 480 6.98917
100 1 605 7.67061
1 62 124 0.908339
2 24 149 1.81668
5 1 212 3.88772
10 1 275 5.377
20 1 360 6.60106
50 1 505 7.83973
100 1 640 8.56562
10
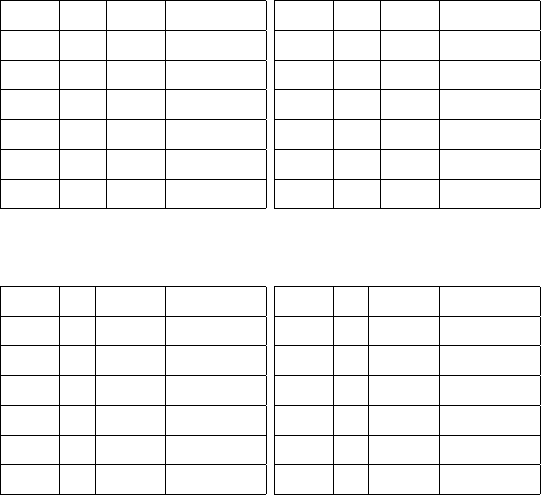
Full pay Jacks or Better video poker with doubling once on every win
1 26 150 1.63572
2 1 196 3.06156
5 1 284 4.90873
10 1 374 6.03806
20 1 486 6.93285
50 1 680 7.84278
100 1 860 8.33571
1 14 157 2.04428
2 1 207 3.65335
5 1 299 5.63043
10 1 390 6.83604
20 1 510 7.78084
50 1 720 8.74025
100 1 910 9.2598
Cryptologic Double Bonus Video Poker
1 1 545 7.1477
2 2 718 7.80724
5 1 1025 8.46746
10 1 1335 8.8471
20 1 1710 9.13194
50 1 2280 9.39536
100 1 2740 9.52055
1 1 574 8.00639
2 2 756 8.70235
5 1 1080 9.39366
10 1 1410 9.79079
20 1 1810 10.0896
50 1 2420 10.3664
100 1 2920 10.5039
11