Wizardに尋ねる #307
2018年の「デッドプール」に参加します。ルールは以下のとおりです。
- 各プレイヤーは、100歳未満の存命の著名人10人のリストを提出しなければなりません。
- 2018年にAP通信の報道で明らかになったように有名人が亡くなった場合、その有名人の名前がリストに載っている人は100-xポイントを受け取る。xは死亡時の年齢。
- 2019 年 1 月 1 日に最も多くのポイントを獲得したプレイヤーが勝利します。
平均から考えると、このゲームに最適な戦略は何でしょうか?
元アクチュアリーとして、適切な方に質問していただきました。アクチュアリー協会が私の回答を職業上の濫用と捉えないよう願っております。とはいえ、ご質問にお答えするために、以前勤務していた社会保障局の首席アクチュアリー室の2014年生命表を参照しました。
期間生命表には、2014 年における任意の年齢および性別の人の死亡確率などが示されています。その情報を使用して、0 から 100 までのすべての年齢および性別の死亡確率と期待ポイントの両方を示す次の表を作成しました。
2014年期間生命表死亡プール
| 年 | 確率 死亡 — 男性 | 確率 死 — 女性 | 期待される ポイント — 男性 | 期待される ポイント — 女性 |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 13 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 25 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 26 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 27 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 28 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 29 | 0.001454 | 0.000648 | 0.103234 | 0.046036 |
| 30 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 32 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 34 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 35 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 36 | 0.001781 | 0。001008 | 0.113970 | 0.064538 |
| 37 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 38 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 39 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 42 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 44 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 47 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 48 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0。073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
表は、90 歳の男性の最大予想ポイントが 1.645220 であることを示しています。
この質問は、私のギャンブル以外のフォーラム「Diversity Tomorrow」で提起され、議論されています。
ルーレットを7,456回スピンして記録しました。結果は以下の通りです。ホイールに偏りがあるのではないかと疑っていますが、このデータがルーレットをプレイするのに十分な決定的な証拠になるかどうかは分かりません。
ルーレットデータ
| 勝利 番号 | 発生事例 |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| 合計 | 7456 |
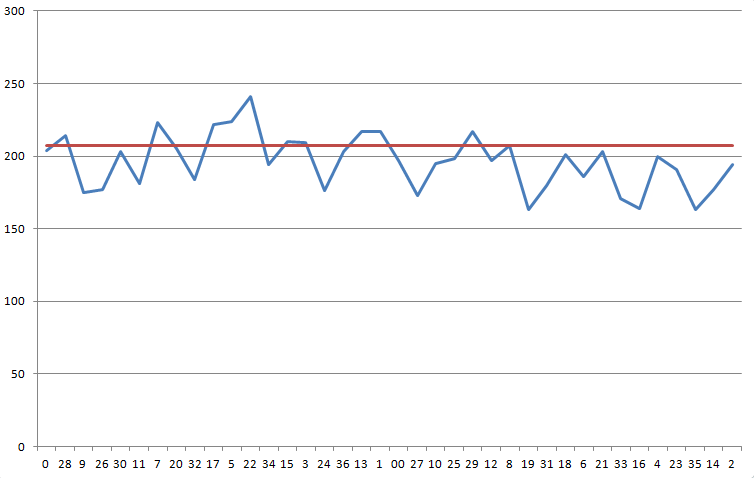
以下のグラフは、ホイールの結果を順番に表示しています。青い線があなたの結果です。赤い線は、5.26%のハウスエッジを克服するために必要な数字、207.11です。
この分布に対するカイ二乗検定では、統計量は68.1、自由度は37となります。この値以上に歪んだ結果が出る確率は725分の1です。
カイ二乗検定は結果の順序を考慮していないため、この状況に最適な検定法ではないと思いますが、これより良い検定法を知りません。コルモゴロフ・スミルノフ検定を提案する人もいますが、私は適切ではないと思います。他に適切な検定法があれば、ぜひ教えてください。
5番の周りの3つの数字のアークに賭けていた場合、記録したスピン数で10.57%の利益があったと言えます。しかし、7つの数字のアークに賭けた場合、その利益は2.84%に低下します。
分かりやすい英語で答えざるを得ないなら、ホイールにはバイアスがあるという証拠はあるものの、合理的な疑いの余地がないほどの証明ではない、と言いたいところです。しかし、そのバイアスだけでは、ハウスエッジを十分かつ確実に克服するには不十分でしょう。カジノがテーブル間でホイールを交換していないと仮定すると、多額のお金を賭ける前に、より多くのデータを収集する必要があると思います。この回答が曖昧で申し訳ありません。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
サムとダンという2人のプレイヤーがそれぞれ5枚のコインを持っています。両者とも1枚から5枚のコインを手札に加える必要があります。同時に、それぞれが出したコインの枚数を公開しなければなりません。もし両者が同じ枚数を選択した場合、サムが勝ち、出したコインをすべて獲得します。もし両者が異なる枚数を選択した場合、ダンが出したコインをすべて獲得します。両プレイヤーが完璧な論理的思考力を持っていると仮定した場合、ダンにとって最適な戦略は何でしょうか?
ダンは次のように戦略をランダム化する必要があります。
- 1枚のコインを選ぶ確率 = 77/548。
- 1枚のコインを選ぶ確率 = 107/548。
- 1枚のコインを選ぶ確率 = 117/548。
- 1枚のコインを選ぶ確率 = 122/548。
- 1枚のコインを選ぶ確率 = 125/548。
この戦略では、サムが何枚のコインを選んだかに関係なく、ダンは毎ターン 3.640510949 枚のコインを獲得できると予想できます。
解答は私の数学問題サイト、問題 230 にあります。
この質問につながった関連する質問は、 Wizard of Vegasの私のフォーラムで見つかります。
サンフランシスコのカリフォルニアグランドカジノでは、「Hot Action Blackjack」というブラックジャックのゲームが行われています。ゲームのルールは以下の通りです。
- 連続シャッフル機を使用した6デック(ジョーカー18枚追加、額面2として扱い)。
- ディーラーはソフト17でヒット。
- 任意の最初の2枚でのダブルダウン可能。
- 最大4ハンドまで再スプリット可能。
- エースへのドローまたはエースの再スプリットは不可。
- サレンダーなし。
- ブラックジャックの配当は6対5。
- プレイヤーの最初の2枚がジョーカーの場合、4対1のボーナスを支払い。
- プレイヤーの最初の2枚がスートの揃ったエースの場合、5対1のボーナスを支払い。
- プレイヤーは参加時に5%のコミッションを支払う必要あり。
基本的な戦略とハウスエッジは何ですか?
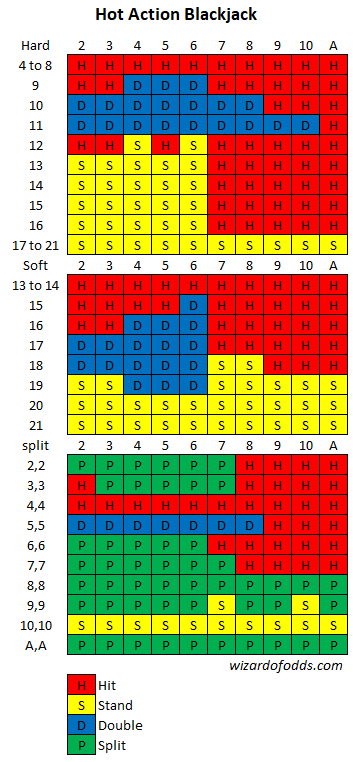
まず、これらのルールに基づく私の基本戦略は以下の通りです。
総合的に考えると、初期賭け金ベースでハウスエッジは6.01%になります(痛い!)。つまり、プレイヤーが100ドルを賭けた場合(5ドルの手数料を除く)、平均的に6.01ドルを失うと予想されます。カリフォルニアのプレイヤー銀行制ゲームには、自分が銀行役でない限り近づかない理由がよくわかりますね。
この質問は、私のフォーラム「Wizard of Vegas」で提起され、議論されています。