ホーム ›
ゲーム ›
ビンゴの確率：ステーションカジノでのジャンボプログレッシブの分析

最終更新日： August 12, 2019

このページ

ビンゴの確率：ステーションカジノでのジャンボプログレッシブの分析

アップデート

私が最初のレポートを書いてから、ステーションカジノは10月のどこかで明らかに再度オッズと偶数の分布を変更しました。次の表は、私が取ったカードと私が「L」と呼ぶ別のカードの最近の分布を示しています。

ジャンボビンゴカードの新しいサンプリング

オッズの数字	マイクのサンプル	Lのサンプル	サンプルの合計	確率
9	2	3	5	0.011261
10	7	10	17	0.038288
11	14	25	39	0.087838
12	34	41	75	0.168919
13	41	71	112	0.252252
14	86	110	196	0.441441
合計	184	260	444	1

9から14オッズの範囲は同じままですが、以前のより均一な分布とは対照的に現在の14オッズに大きく重み付けされています。オッズが高くなるとプログレッシブジャックポットを獲得するのが難しくなるので、このサンプリングに基づいて正の期待値が必要な場合はジャンボボールが54に達するまで待つことをお勧めします。

次の表は、私の合計サンプルを同じサンプルサイズとステファン L. カバレロ（ステーションカジノのエグゼクティブバイスプレジデント兼最高執行責任者）が以前に説明した同じカードの描画方法を想定した場合のそれぞれの合計の確率と比較しています。

実物 Vs. 期待値の合計

オッズの数字	サンプルの合計	期待値の合計
9	5	33.17
10	17	60.48
11	39	87.61
12	75	101.15
13	112	93.18
14	196	68.41
Total	444	444

これは私の結果が期待していたものと一致していないことを明らかにします。期待値と比較したこの分布の歪度に関する統計的検定では5自由度のカイ2乗統計量330.71が得られ、これ以上の歪んだ結果の確率は402,433,741,048,496,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000に1の確率です。これを概観することでパワーボールを8回続けて打つ確率が高くなります。

さらにこれを議論するためにカードの描画方法に変更がありました。次の表は変更の前後の私のサンプルの結果を示しています。サンプル1は8月でサンプル2は10月30日と11月1日に採取されています。

過去 Vs. 新しいサンプル

オッズの数字	サンプル1	サンプル2	サンプル1の確率	サンプル2の確率
9	35	5	13.51%	1.13%
10	35	17	13.51%	3.83%
11	34	39	13.13%	8.78%
12	48	75	18.53%	16.89%
13	55	112	21.24%	25.23%
14	52	196	20.08%	44.14%
合計	259	444	100%	100%

次のグラフは、予想される確率と比較した際の上記2つの確率列の表を比較しています。

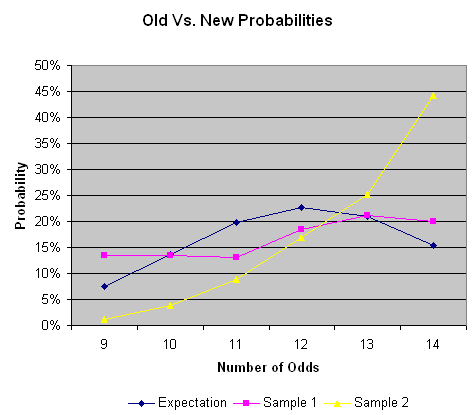
これが示すのは、サンプル1が期待値とよく一致しなかったもののその偏差がサンプルの偏りによるものである可能性があること（この確率は4844年に1回）です。ただし新しいサンプリングは、疑いの余地なく期待値または古いサンプルのいずれとも一致しません。

新しいカードがステーションカジノの経営陣にどのように引き出されるかについて質問したところ、カードの引き方に変更はないと言われました。それとは反対の私の証拠についてはコメントがなく、私の「否定的な報告」の為のそれ以上の協力は拒否されました。

注：「マイクのサンプル」は、11月1日3時のサンセットステーションでのセッションで収集されました。「Lのサンプル」は、ボルダーステーションの10月30日の午前9時と午前11時のセッションで収集されました。

以下は私が行った最初の研究ですが、すでにそれらは時代遅れになっています。

以下は、次のラスベガスのカジノで販売されているプログレッシブビンゴカードが完全にランダムに作成されていないという私の証拠です。

パレスステーション
サンタフェステーション
テキサスステーション
ボルダーステーション
サンセットステーション
フィエスタランチョ
フィエスタヘンダーソン
サムズタウン

ラスベガスのステーションカジノでは、ジャンボビンゴと呼ばれるリンクされたビンゴプログレッシブが行われています。プログレッシブメーターは100,000ドルから始まり、プレイヤーが勝つには47回のコールで全カバー（カード上の24の数字全て）を得る必要があります。最初の週に5つのビンゴパーラーのいずれにもヒットしなかった場合、プログレッシブ（ジャンボボールと呼ばれる）を獲得するための呼び出し数は1から48に増加します。同様に、ジャンボボールは誰かが勝利するまで毎週1ずつ増加します。

あなたの時間を節約するために言いますが、呼び出される最初の37の番号の2から74までは全て偶数です。ジャンボビンゴカードは全ての偶数に対して便利に事前にマークされており、ゲームが始まると発信者はすべて偶数のカードに基づいて誰かが勝ったかどうかを尋ねます。次に、誰も勝ちカードを要求しなかった後、発信者は偶数番号のボールを無視してランダムにボールを引きます。ジャンボボールがコールされるまでに誰もカバーオールを受け取らなかった場合のコールの数に関係なく、最初の人がカバーオールを獲得するための賞金が1199ドルであると誰も主張しない場合は52コール以内にカバーオールに対して5000ドルの慰め賞金があります。そしてその他のビンゴと同じように、複数のプレイヤーが同時に勝った場合には賞金は分割されます

フィエスタのカジノは小規模で非常によく似たゲームを持っています。プログレッシブは25,000ドルから始まり、慰め賞金はそれよりも少なくなります。全ての偶数が事前に呼び出されるという点でも同じで、サムズタウンでは事前に呼び出された奇数によってゲームが逆転します。

次の表は、フェアカードのカードの奇数の合計に応じた確率分布を示しています。私のフェアカードの定義としては5つの「B」番号が1から15までランダムに選択され、5つの「I」番号が16から30までランダムに選択されるというものです。同じ結果を達成する別の方法は、数字が選択されたときにカードを埋める1から75までの数字を描くことで、対応する列がすでに埋められている場合の数字を無視することです。

奇数の合計の確率 - フェアカード

オッズの数字	確率	逆の確率
0	0.000000000436	2293355030に1
1	0.000000022747	43962077に1
2	0.000000534794	1869877に1
3	0.000007530006	132802に1
4	0.000071202834	14044に1
5	0.000480801205	2080に1
6	0.002407676276	415に1
7	0.00916827051	109に1
8	0.027013789916	37に1
9	0.062346657338	16に1
10	0.113677702037	9に1
11	0.164671200005	6に1
12	0.1901222602	5に1
13	0.175132872532	6に1
14	0.1285740634	8に1
15	0.074984221403	13に1
16	0.034540809008	29に1
17	0.012458867878	80に1
18	0.003475365511	288に1
19	0.00073657509	1358に1
20	0.000115624911	8649に1
21	0.000012937867	77292に1
22	0.000000969822	1031117に1
23	0.000000043401	23041075に1
24	0.000000000872	1146677515に1
合計	1	1に1

極端にオッズが少ないカードは、確かに良いスタートを切りほとんどオッズのカードよりも勝つ可能性がはるかに高くなります。ラスベガスアドバイザーの2002年7月号では、カードがランダムに作成されたという仮定に基づいてジャンボビンゴに関する記事を書きましたが、そのコラムのある読者は彼が1500枚のカードを購入してそれら全てのオッズの総数が9から14であったことからも明らかなようにカードはランダムに作成されたものではないと信じていると私に言いました。

全てのカードのオッズが9〜14であるという告発を確認するために、アシスタントのロブフェルドハイムがパレスステーションで259枚のジャンボビンゴカードを集めました。次に各カードのオッズ数を数えましたが、オッズの合計は常に9〜14でした。次の表は、各オッズ数の合計とフェアゲームで期待される合計を示しています。

パレスステーションカードの実物 vs. 期待値

オッズの数字	サンプルの数字	期待値の合計
0	0	0
1	0	0.000006
2	0	0.000139
3	0	0.00195
4	0	0.018442
5	0	0.124528
6	0	0.623588
7	0	2.374582
8	0	6.996572
9	35	16.147784
10	35	29.442525
11	34	42.649841
12	48	49.241665
13	55	45.359414
14	52	33.300682
15	0	19.420913
16	0	8.94607
17	0	3.226847
18	0	0.90012
19	0	0.190773
20	0	0.029947
21	0	0.003351
22	0	0.000251
23	0	0.000011
24	0	0
合計	259	259

オッズの総数が9から14の間になる確率は0.834524756です。42.858088のサンプルのうち、それは9から14の範囲外にあるはずですがどれもそうではありませんでした。公正なゲームでこれが発生する確率は0.834524756259 = 4.4953 * 10-21で、つまり222,454,364,282,805,000,000分の1になります。

以下は、2002年8月22日の午前11時のセッション後にフィエスタランチョにて取得されたグランデビンゴカードで行われた同じ種類のテスト結果です。

フィエスタランチョカードの実物 vs. 期待値

オッズの数字	サンプルの数字	期待値の合計
0	0	0
1	0	0.000002
2	0	0.000047
3	0	0.000655
4	0	0.006195
5	0	0.04183
6	0	0.209468
7	0	0.79764
8	0	2.3502
9	10	5.424159
10	6	9.88996
11	19	14.326394
12	18	16.540637
13	18	15.23656
14	16	11.185944
15	0	6.523627
16	0	3.00505
17	0	1.083922
18	0	0.302357
19	0	0.064082
20	0	0.010059
21	0	0.001126
22	0	0.000084
23	0	0.000004
24	0	0
合計	87	87

9から14の範囲外になると予想される数は14.396346ですが実際にはほぼ0で、この確率は1.46289 * 10-7で6,835,771分の1になります。

次は、サムズタウンからのプログレッシブカードのサンプル結果です。

サムズタウンカードの実 vs. 期待値

オッズの数字	サンプルの数字	期待値の合計
0	0	0
1	0	0.000002
2	0	0.000055
3	0	0.000768
4	0	0.007263
5	0	0.049042
6	0	0.245583
7	0	0.935164
8	1	2.755407
9	1	6.359359
10	19	11.595126
11	25	16.796462
12	24	19.392471
13	20	17.863553
14	12	13.114554
15	0	7.648391
16	0	3.523163
17	0	1.270805
18	0	0.354487
19	0	0.075131
20	0	0.011794
21	0	0.00132
22	0	0.000099
23	0	0.000004
24	0	0
合計	102	102

ステーションカジノのスティーブンL.カヴァッラーロとの会話に基づいた結果、サムズタウンでは10から15のオッズや9から14の偶数の範囲を期待していましたが、実際には8つの偶数で1枚のカードを取得して9で1枚しか得ることが出来ませんでした。8から14の偶数を持つカードの確率は0.881703で102がこの範囲に入る確率は2.647786 * 10-6、つまり377,674に1になります。

さらにサンコーストの通常のビンゴカードでも同様のテストを行った結果、129のサンプルでは次の実際の結果と期待される結果が得られました。

サンコーストカードの実物 vs. 期待値

オッズの数字	サンプルの数字	期待値の合計
0	0	0
1	0	0.000003
2	0	0.000069
3	0	0.000971
4	0	0.009185
5	0	0.062023
6	0	0.31059
7	1	1.182707
8	6	3.484779
9	5	8.042719
10	17	14.664424
11	19	21.242585
12	29	24.525772
13	20	22.592141
14	18	16.586054
15	10	9.672965
16	1	4.455764
17	3	1.607194
18	2	0.448322
19	0	0.095018
20	0	0.014916
21	0	0.001669
22	0	0.000125
23	0	0.000006
24	0	0
合計	129	129

129枚のカードのうち、9から14の範囲外の数は21で予想される数は21.34630654でした。これらのカードは奇数/偶数テストに簡単に合格していますが、彼らにはオッズや偶数が事前に呼び出されるゲームがなかったので当然の結果だと思います。

次の表は、プレイヤーが全ての50の数字の範囲内でカバーを取得する必要がある場合の公正なゲームで勝つ確率を示しています。

勝率 - フェアカード

オッズの数字	カードの確率	勝ちカードの確率	確率の合計
0	0.000000000436	1	0.000000000436
1	0.000000022747	0.342105263158	0.000000007782
2	0.000000534794	0.110953058321	0.000000059337
3	0.000007530006	0.033902323376	0.000000255285
4	0.000071202834	0.009686378107	0.000000689698
5	0.000480801205	0.002564041264	0.000001232794
6	0.002407676276	0.000621585761	0.000001496577
7	0.00916827051	0.000135971885	0.000001246627
8	0.027013789916	0.000026317139	0.000000710926
9	0.062346657338	0.00000438619	0.000000273464
10	0.113677702037	0.000000604992	0.000000068774
11	0.164671200005	0.000000064821	0.000000010674
12	0.1901222602	0.000000004802	0.000000000913
13	0.175132872532	0.000000000185	0.000000000032
14	0.1285740634	0	0
15	0.074984221403	0	0
16	0.034540809008	0	0
17	0.012458867878	0	0
18	0.003475365511	0	0
19	0.00073657509	0	0
20	0.000115624911	0	0
21	0.000012937867	0	0
22	0.000000969822	0	0
23	0.000000043401	0	0
24	0.000000000872	0	0
合計	1	0	0.000006053319

下の画像の右のセルは勝率が0.000006053319、つまり165199に1であることを示しています。フェアゲームで勝った場合は、オッズが6のカードで発生する可能性が最も高いです。オッズが9未満のフェアゲームで勝つカードの確率は94.15％です。

私は自分の調査について書くことを計画していることを知った際にスティーブンL.カヴァッラーロ（ステーションカジノのエグゼクティブバイスプレジデント兼最高執行責任者）とジョナサンスウェイン（パレスステーションのバイスプレジデント兼ゼネラルマネージャー）に会うように頼まれました。スティーブンはすぐに出てきて、カードがそれぞれ9から14のオッズを含むように事前に選択されていることを認めました。彼が述べるのは、これは競争の場を平準化して各カードと顧客に勝つ希望を与えるための努力であるそうです。また彼は、最初は範囲がはるかに広く、最初の勝者は最初にカードのオッズが3つしかなかったと述べました。さらにサムズタウンカジノとフィエスタカジノでも同じことをしており、ステーションゲームはネバダゲーミングコントロールボードによって完全に承認されていると彼は言いました。

スティーブン・カヴァッラーロのフォローアップの電話では、コンピューターがランダムに一連の公正な番号によってカードが選択されると私に言いました。合計オッズが9から14の間の場合にはカードがプリントされ、それ以外の場合はその数字のセットが破棄されて次のセットに進みます。次の表は、このカード作成方法での各オッズ数の調整済み確率を示しています。

ステーションカードのオッズ合計数の確率

オッズの数字	確率
9	0.074709
10	0.136218
11	0.197323
12	0.227821
13	0.209859
14	0.154069
合計	1

全体としてはミックスから最高のカードを削除した結果、特定のカードがプログレッシブに当たる確率は大幅に低くなります。最悪のカードを削除しても補償されず、カードを事前に選択するというこのポリシーによってジャックポットが大きくなり、同時にカジノはメーターを再シードする頻度を減らす必要があります。最終的な結果としては、進歩的な勝者が少なくなって獲得した賞金の合計も減ります。次の表は、ジャックポットを獲得するために呼び出されたボールの数に応じて、フェアカードとステーションカードの両方が勝つと予想される確率を示しています。

勝利期待値

コールされる数字	フェアカード	ステーションカード	比率
47	1,122,373に1	205,287,873に1	182.91
48	583,217に1	35,037,983に1	60.08
49	308,005に1	8,203,638に1	26.63
50	165,199に1	2,358,363に1	14.28
51	89,925に1	785,008に1	8.73
52	49,648に1	291,923に1	5.88
53	27,784に1	118,433に1	4.26

比率の列が示すのは、フェアカードとは対照的にステーションカジノカードを使用して勝つことが何倍難しいかです。例えば、ジャックポットを50ボール以下でヒットする必要がある場合での勝利は14.28倍難しくなります。

私の意見としては、全てのビンゴカードは上記の方法で実際にランダムに作成する必要があります。それを除いてカードがランダムに作成されない場合は、カードの作成方法とプレイヤーへの影響に関するルールを開示する必要があると思います。私はあらゆる形態のギャンブルにおいて公平性と開示を強く支持しており、これらのどちらもネバダ州のビンゴには当てはまりません。ビンゴをプレイする方はぜひそれを心に留めておいてください。

スティーブン・カヴァッラーロとジョナサン・スワイムとの出会いとこの問題について開示的になってくれたことに心から感謝します。

ビンゴの確率に戻る

Michael Shackleford, ASA