Wizardに尋ねる #227
3年前のAsk The Wizardコラムで、あなたはこう書いていました。「サイコロに影響を与えるかどうかの賛否を論じるには500回では少なすぎるというのはその通りですが、500回投げた方がゼロよりはましです。」 実験において、サイコロに影響を与えるとされる人物に、多額の賭け金を賭けるのに十分な自信を持つためには何を求めるでしょうか? ブラックジャックのシミュレーションでは、10億ラウンドが「信頼できる」結果の目安となるからです。あなたが考えられる最も効率的な(つまり、最小限の回数で済む)実験設計では、シューターは結果に影響を与えていると確信するために、何回振る必要があるでしょうか? 答えはシューターのスキル次第だとは思いますが、私の言いたいことはお分かりでしょう。最良のシナリオでも100万回も振る必要があるなら、それは無駄な努力になるでしょう。
信頼が得られる明確な基準はありません。それは程度の問題です。まず、何をテストしているのか、そして射手はどのような結果になると予測しているのかを尋ねます。どんなテストでも、2つの誤りが生じる可能性があります。熟練した射手が不運で失敗するか、あるいは偶然射手が幸運で合格するかです。この2つのうち、私は偽陽性を避けたいと考えています。合理的なテストであれば、偽陰性の確率は約5%、偽陽性の確率は約1%に設定できると思います。
例えば、申請者がサイコロを7回振るごとに平均1回7が出ると主張したとします。ランダムシューターは平均して6回に1回7が出ます。試行錯誤の結果、これらの基準の両方を満たすテストは、サイコロを3,600回振り、合格に必要な出目が547回以下、つまり6.58回振るごとに1回7が出るという結果になりました。
7人に1人のシューターは、平均514.3個の7を投げ、標準偏差は21.00です。ガウス近似を用いると、そのような熟練シューターが548個以上の7を投げる確率(偽陰性)は5.7%です。ランダムシューターは平均600個の7を投げ、標準偏差は22.36です。ランダムシューターがテストに合格する確率(偽陽性)は0.94%です。下のグラフは、熟練シューターとランダムシューターの可能性のある結果を示しています。結果が緑の線より左側にある場合、私はそのシューターがテストに合格したと見なし、彼に賭けます。
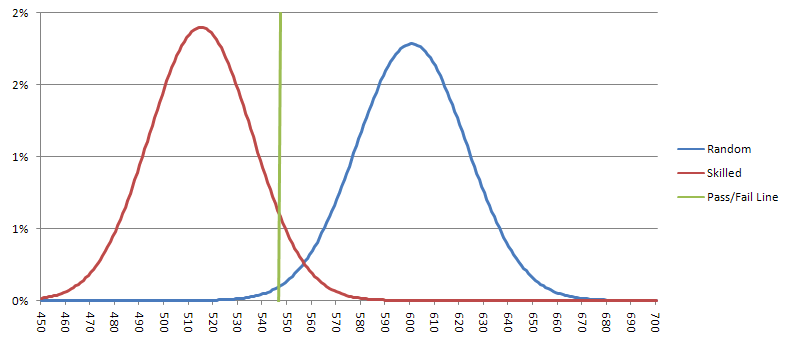
現実的なジレンマは、1分間に2回投げると仮定すると、テストの実施に30時間かかるということです。有意水準をもっと緩く設定して所要時間を短縮することもできるかもしれませんが、結果はそれほど説得力のあるものにはならないでしょう。500ロールのウォン実験よりも大規模なテストを行う時期が来ていると思います。
ラッキーレディサイドベットを、例えばトゥルーカウントが10以上の場合にのみプレイした場合、ハウスエッジを回避できますか?もしそうなら、このサイドベットでハウスエッジを回避できる最低のトゥルーカウントはいくつですか?
私自身は、この賭けにおけるカードカウンティングの効果を研究していません。しかし、アーノルド・スナイダーは研究しており、その結果は著書『ビッグブック・オブ・ブラックジャック』に掲載されています。その中で彼は、6デッキのゲームでは、最後の2デッキで、レッドセブンカウントを用いて+10以上のカウントが出た場合に賭けるべきだとしています。ダブルデッキのゲームでは、最後の2デッキで、+6以上のカウントが出た場合に賭けるべきだとしています。
6デッキのシューでレイトサレンダーが許可された場合、ハウスがソフト17をヒットした場合、そしてハウスがソフト17でスタンドした場合、プレイヤーはどのような利益を得られますか?8デッキのシューの場合はどうでしょうか?
そういった疑問への答えは、私のハウスエッジ計算機を使って、ルールを変えてハウスエッジへの影響を観察することで得られます。普段なら皆さんにやってもらうのですが、今日はちょっと我慢できるので、ここに載せておきます。
6デッキ、ディーラーがソフト17でスタンド: 0.0726%
8デッキ、ディーラーがソフト17でスタンド: 0.0758%
6デッキ、ディーラーがソフト17でヒット:0.0882%
8デッキ、ディーラーがソフト17でヒット:0.0916%
バカラでプレイヤーに賭けることで、任意のポイントから10ユニットを失うのにかかる平均試行回数を計算する方法があるかどうかを疑問に思いました。
8デッキを想定したプレイヤーベットのハウスエッジは1.2351%で、10ユニットを失うのに必要な予想ハンド数は10 / 0.012351 = 809.66です。
先日、家族とホームポーカー(オマハ・デュース・ワイルド)をやっていました。5人のプレイヤーがいて、2人になってしまいました。私はそのうちの1人でした。もう1人のプレイヤーは一晩中勝ち続けていました。ようやく良い手ができました。私は相手の方を見て、からかうように「フォーセブン」とコールしました。すると彼女はエースを4枚持っていると言い、チップをレーキし始めました。私は訂正し、ストレートフラッシュだと伝えました。すると彼女は、私がすでにフォーセブンをコールしたと言いました。私は自分の手を見せましたが、彼女はまだ私がすでにフォーセブンをコールしたと主張し、私の手はもう良くないと言いました。では、誰が勝ったのかという疑問が生じます。ストレートフラッシュはフォーカードに勝つのは明らかです。しかし、私があのようなことを言ったことで、自分の手札をマックしたのでしょうか?お金はまだテーブルの上にあります。
結局のところ、カードがすべてを物語る。君はそのハンドに勝つべきだった。


