Wizardに尋ねる #230
今日のニュースでは、アトランティックシティの女性がボルガータでサイコロを154回連続で振って7が出たそうです。つまり、彼女は2つのサイコロを154回振って、7が出なかったということです。そこで私は (30/36) 154 を取って、1.5兆分の1以上のオッズを算出しました。メガミリオンズの宝くじに当たる可能性は、サイコロを154回連続で7以外の目が出るマラソンをするよりも約9,000倍も高いのです。これがいかに天文学的な確率の低さか、そしてDNA鑑定の偽造の可能性がわずか数十億分の1しかないことを考えると、あなたはどの程度不正を疑い、この件についてボルガータに相談しようとしますか？私はすでにボルガータに電話して自分の名前を伝え、好きにやってくれと言いました。あなたの考えを聞かせてください。
まず、彼女は合計 154 回サイコロを振り、154 回目は 7 が出ました ( 出典: NJ.com )。しかし、これは最初の 153 回で一度も 7 が出なかったという意味ではありません。カムアウト ロールで何度も 7 が出ていた可能性もあります。2003年 5 月 3 日のコラムで示したように、 154 回目まで投げる確率は 56 億分の 1 です。メガ ミリオンズに当たる確率は、(56,5)*46 = 175,711,536 分の 1 です。つまり、154 回以上投げるのは約 32 倍難しいということです。十分な時間とテーブル (おそらく存在する) があれば、このようなことは遅かれ早かれ起こるはずでした。ですから、私は不正行為を疑うことはありません。このようなことが起こる確率は、どの年でも約 1% だとおおよそ見積もっています。
また、行列で表現された私の解答は、 mathproblems.infoの問題 204 で参照してください。
ステーション カジノでは、ビンゴ プレイヤーの支出額に応じて、次のように無料の「Mini X」ビンゴ カードを提供しています。
1ドルから19ドルまでご利用の場合、無料カード1枚
20ドルから29ドルをご利用の場合 = 無料カード2枚
30ドルから39ドルをご利用の場合 = 無料カード3枚
40ドルから49ドルをご利用の場合 = 無料カード4枚
50ドルから59ドルをご利用の場合 = 無料カード5枚
60ドル以上お買い上げで6枚の無料カード
各カードには5つの数字があり、それぞれビンゴの文字に対応しています。賞品は以下の通りです。
カバーカード5桁 = 10,000ドル
カバーカード6桁 = 3,000ドル
カバーカード7桁 = 500ドル
7 桁以下の数字を誰もカバーしなかった場合、最初にカバーしたプレイヤーに 50 ドルの慰謝料が支払われます。
次の表は、基本賞金の価値がカード 1 枚あたり 1/5 セントであることを示しています。
Mini Xカードの期待値
| 通話 | 支払う | 確率 | 戻る |
| 5 | 10000 | 0.00000006 | 0.00057939 |
| 6 | 3000 | 0.00000029 | 0.00086909 |
| 7 | 500 | 0.00000087 | 0.00043455 |
| 合計 | 0.00000122 | 0.00188303 |
1枚のカードの慰めの賞金の価値は50/nです。ここでnは競合カードの枚数です。例えば、競合カードが1000枚ある場合、1枚の慰めの賞金の価値は5セントになります。
ビデオポーカーのダブルダブルボーナスポーカー戦略ページでは、5が配られた場合、
6 7 8 9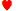
ストレートを握るのが正しいと。直感に反しているように思えるのですが、ストレートフラッシュを狙うのがなぜ悪い戦略なのか、もう少し詳しく説明していただけるとありがたいです。
ダブルダブルボーナスでは、ストレートフラッシュは50、フラッシュは6、ストレートは4の配当となります。ストレートフラッシュの確率は2/47、フラッシュの確率は7/47、ストレートの確率は5/47です。つまり、9を捨てた場合の期待配当は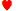(2/47)×50 + (7/47)×6 + (5/47)×4 = 3.4468。4のストレートの期待リターンははるかに高くなります。
ラスベガスのカードゲーム「3-5-7」はどうなったのでしょうか？どこにも見つかりません。
このゲームは特許侵害にあたるため、アメリカのカジノから撤去されたと聞きました。ネバダ州ゲーミング管理委員会の2008年第4四半期統計報告書によると、クラーク郡におけるテーブルゲームの数は以下のとおりです。
クラーク郡テーブルゲーム数
| ゲーム | テーブル |
|---|---|
| 21 | 2537 |
| ルーレット | 405 |
| クラップス | 334 |
| 他の | 243 |
| バカラ | 233 |
| スリーカードポーカー | 208 |
| パイゴウポーカー | 194 |
| ミニバカラ | 143 |
| そのままにして置け | 98 |
| パイゴウ | 80 |
| ホイール・オブ・フォーチュン（ビッグシックス） | 37 |
| カリビアンスタッドポーカー | 22 |
| シックボー | 1 |
| チャック・ア・ラック | 1 |
残念ながら、243 の「その他の」ゲームが何であるかは述べられていないため、これはあなたの質問に答えるのにあまり役立ちませんが、それでも言及する価値はあります。
拝啓、自動シングルゼロルーレットを8672回「計測」しました。すると、なんと私が事前に決めていた数字が278回も出ました。ポケットの摩耗具合を考慮してこの数字を選びました。この数字の確率が1/37よりも高いと確信できますか？
私の用語が正しければ、「ホイールをクロッキングする」とは、ボールの速度、位置、ホイールの速度から判断して、ボールがどこに落ちるかを予測することを意味します。あなたがやっていることは、偏りのあるホイールを悪用しているように聞こえますが、これは別のアドバンテージプレイです。話が逸れているなら、3つ目のアドバンテージプレイは「ディーラーシグネチャー」を悪用することです。これは、ディーラーが非常に安定しているため、ボールとホイールの速度が毎回ほぼ同じである状況です。これにより、プレイヤーはボールの位置と過去の結果に基づいて、ボールがどこに落ちるかを予測できます。
ご質問にお答えすると、期待される当選回数は8672/37=234.38回です。分散は8672×(1/37)×(36/37)=228.04です。標準偏差は分散の平方根で、15.10です。予想よりも278-234.38=43.62回多く当選しました。つまり、(43.62-0.5)/15.10=2.8556標準偏差です。0.5を差し引く理由は説明が難しいですが、連続関数を用いて離散関数を推定する際の調整係数だと言えるでしょう。ガウス近似を用いると、期待される当選回数以上当選する確率は0.21%です。つまり、偏りのあるホイールを見つけた可能性が高いと言えます。しかし、それが単なる幸運だった可能性は 466 分の 1 残っています。