Wizardに尋ねる #253
いい質問ですね。他の読者のために、2人プレイでこれらの2つのスターティングハンドをランダムに選んだ場合のオッズを以下に示します。
KJ スーツ vs. A-7 オフスーツ
| 手 | 勝つ | 失う | 描く | 期待値 |
K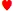 J J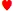 | 0.6148 | 0.3634 | 0.0218 | 0.2513 |
あ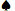 7 7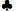 | 0.5717 | 0.3949 | 0.0334 | 0.1768 |
ただし、私の 2 人用テキサス ホールデム 計算機によると、これら 2 つのハンドが対戦する確率は次のとおりです。
A7の勝利 = 53.52%
KJの勝利 = 46.10%
同点 = 0.39%
つまり、私の表ではKJスーツの方が上位にランクされていますが、A7アンスーツと直接比較すると下位にランクされています。なぜでしょうか?
答えを説明するのは難しいです。2つのハンドが互いに対戦する場合、それらの相互作用を考慮する必要があります。例えば、スターティングハンドの強さの表では、AKオフスーツはAQオフスーツよりもわずかに優れており、期待値はそれぞれ.3064と.2886です。しかし、実際に両者を対戦させると、AKがAQを圧倒します。その強さは次のように表せます。
AKの勝率 = 71.72%
AQの勝利率 = 23.69%
同点 = 4.58%
A7オフスーツとKJスーツでは、エースがキングとジャックよりも高くなっています。KJプレイヤーが勝つ可能性が最も高いのは、KまたはJでペアになり、エースが出ない場合です。その確率はわずか37.73%です。残りの46.10%のKJの勝率は、より高いハンドから生じます。
A7 は KJ に対して強いですが、ランダムハンドでは KJ よりも優位に立つことが多いです。
もしかしたらこれはあまり良い例えではないかもしれませんが、じゃんけんのゲームに似ています。熟練したプレイヤー同士であれば、それぞれの投げる力はほぼ同じになるはずです。しかし、片方のプレイヤーが紙を投げ、もう片方のプレイヤーがハサミを投げると、力の差は意味をなさなくなり、ハサミが勝ちます。
ラスベガスのビッグホーンとロングホーンでは、ブラックジャックで3枚のカードでダブルダウンが認められています。このルールでは、何か戦略を変えるべきでしょうか?
私の Wizard of Vegas サイトの読者は、ディーラーがソフト 17 をヒットする標準的なマルチデッキ戦略に対して、次の変更を加える必要があると述べています。
- ソフト13をヒットする。5または6に対して
- 2枚のソフト15対4をヒット
- ヒット3,3対2
ソフトハンドをヒットする理由は、ヒット後により良いソフトダブルが手に入る可能性があるからです。このルールでは、エースが出れば3枚のカードで良いダブルになるため、3枚のカードをヒットする価値が高くなります。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
コインを 100 回投げた場合、少なくとも 1 回は 7 回連続で表が出る可能性はどれくらいでしょうか。
簡単な非再帰的な式で答えられるかどうかは分かりませんが、簡単な再帰的な式はあります。
f(n)= pr(最初の投げで表が出る)×f(n-1) +
pr(1回目の投げで表、2回目の投げで裏)×f(n-2) +
pr(最初の2回で表、3回目で裏)×f(n-3) +
pr(最初の3回で表、3回目で裏)×f(n-4) +
pr(最初の4回で表、4回目で裏)×f(n-5) +
pr(最初の5回で表、5回目で裏)×f(n-6) +
pr(最初の6回で表、6回目で裏)×f(n-7) +
pr(最初の7回の表) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
どこ:
f(n) = n回のフリップ内で成功する確率。
pr(x) = xが起こる確率。
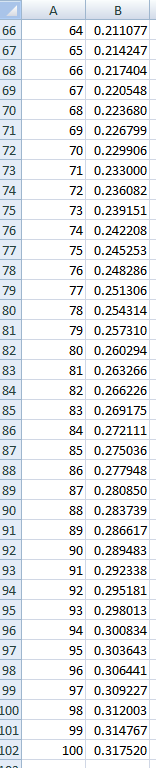
スプレッドシートはこのような問題に最適です。下のスプレッドシートのスクリーンショットでは、セルB2からB8に確率0を設定しています。これは、6回以下の投げ方で7回連続で表が出ることはないためです。セルB9には、次の数式を入力しました。
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
次に、セルB10からセルB102にコピー&ペーストしました。これは100回の投げに相当します。その確率は0.317520です。ランダムシミュレーションで確認しました。
 |  |
この記事が最初に公開された後、リック・パーシー氏が行列代数の解法を私と共有してくれました。以下に私の言葉で解説します。読者は既に行列代数の基礎をご存知であると想定しています。
まず、フリッパーがどの時点でも取り得る状態は 8 つあります。
p 1 = 現在の時点からさらに 7 回表が出た場合の成功確率。
p 2 = 現在の時点からさらに 6 回表が出た場合の成功確率。
p 3 = 現在の時点からさらに 5 回表が出た場合の成功確率。
p 4 = 現在の時点からさらに 4 回表が出た場合の成功確率。
p 5 = 現在の時点からさらに 3 回表が出た場合の成功確率。
p 6 = 現在の時点からさらに 2 回表が必要な場合の成功確率。
p 7 = 現在のポイントからさらに 1 回表が必要な場合の成功確率。
p 8 = それ以上表が必要ない場合の成功確率 = 1。
最大行列S n を、n回目の投げの後に各状態になる確率として定義しましょう。S 0 は最初の投げの前の確率を表し、状態0になる確率は100%です。つまり、S 0 =
| 1 0 0 0 0 0 0 0 |
Tを2つの連続する反転、つまりS nからS n+1への変換行列とする。ここでS n+1 = T × S n
- 状態 1 の場合、1 回の投げ後に状態 2 (表) になる確率は 0.5、状態 1 (裏) のままになる確率は 0.5 です。
- 状態 2 の場合、1 回投げると状態 3 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 3 の場合、1 回投げると状態 4 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 4 の場合、1 回の投げ後に状態 5 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 5 にいる場合、1 回投げた後、状態 6 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 6 の場合、1 回の投げ後に状態 7 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 7 の場合、1 回の投げ後に状態 8 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 8 の場合、成功を達成しており、確率 1.0 で状態 8 のままになります。
これらを遷移行列Tの形で表すと、
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
1 回のめくり後の各状態の確率を取得するには...
(1) S1 = S0 ×T
2回めくってからはどうでしょうか?
(2) S2 = S1 ×T
式(1)を式(2)に代入してみましょう。
(3) S 2 = S 0 × T × T = S 0 × T 2
3回めくった後はどうですか?
(4) S 3 = S 2 × T
式(3)を式(4)に代入すると…
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
100 回目のフリップ後、州までこれを続けることができます...
S 100 = S 0 × T 100
では、T 100とは何でしょうか?コンピュータが登場する前は、このような計算は大変な苦労だったに違いありません。しかし、ExcelのMMULT関数とコピー&ペーストを駆使すれば、T 100 = という式が得られます。
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
右上の項は、100 回のフリップ後に状態 8 になる確率を示しており、0.317520 です。
最近、トスカニーカジノで30日間でブラックジャックを30回出せば100ドルのボーナスがもらえるというプロモーションがありました。当初はカードにスタンプを押すための最低ベット額は5ドルでしたが、その後、スタンプの最低ベット額が15ドルに引き上げられたと聞きました。私はカジノのマネージャーに苦情の手紙を書き、その一部は次のように述べました。
もしこれが事実なら、この変更に大変残念に思います。このプロモーションを利用する機会は一度もありませんでしたし、今後も利用できないのではないかと思います。ブラックジャックを30回獲得するのに必要な時間(約8時間連続プレイが必要と言われています)は、プロモーションでは依然として1ハンドあたり15ドルですが、1ハンドあたり100ドルというのは無理があるように思います。
私が受け取った返信は次のとおりです。
ブラックジャックのブラックアウトプロモーションに関するメールへの返信です。ブラックアウトカードの完成にかかる時間に関する情報をどこで入手されたのか分かりません。4時間以内にカードを完成させたプレイヤーもいらっしゃいます。また、カードの完成期限は30日間です。それだけの時間があれば達成できない目標ではないことをご理解いただければ幸いです。お手紙をいただき、ありがとうございます。お客様からのフィードバックを伺えて大変嬉しく思います。ぜひお試しいただき、賞金を獲得してください!
4 時間以内に 30 回ブラックジャックが出る確率はどれくらいでしょうか?
私のゲーム比較によると、ブラックジャックのプレイヤーは1時間あたり約70ハンドをプレイします。6デッキゲームでブラックジャックが出る確率は、24*96/combin(312,2)=4.75%です。ブラックジャックで引き分けになった場合でもスタンプが押されると仮定すると、カードが満杯になるまで約30/0.0475=632ハンド、つまり9.02時間かかります。
4時間でカードを埋める確率は、280ハンドと仮定すると、一度に1ハンドずつプレイした場合、3万分の1です。4時間で目標を達成したプレイヤーは、少なくとも一度に2ハンドはプレイしていたと推測します。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。


