Wizardに尋ねる #261
シーズンが進み、天候が悪化し、チームの最近のパフォーマンスに関する情報が増えるにつれて、フットボールのトータルベッティングにはどのような力学が影響するのでしょうか?ラインのエラーを見つけるのはどれくらい簡単(または難しい)でしょうか?
この質問に答えるために、私は 1983 年から 2009 年までの各シーズンに基づいて、NFL の週番号別に獲得した平均ポイントをグラフ化しました。次のグラフは結果を示しています。
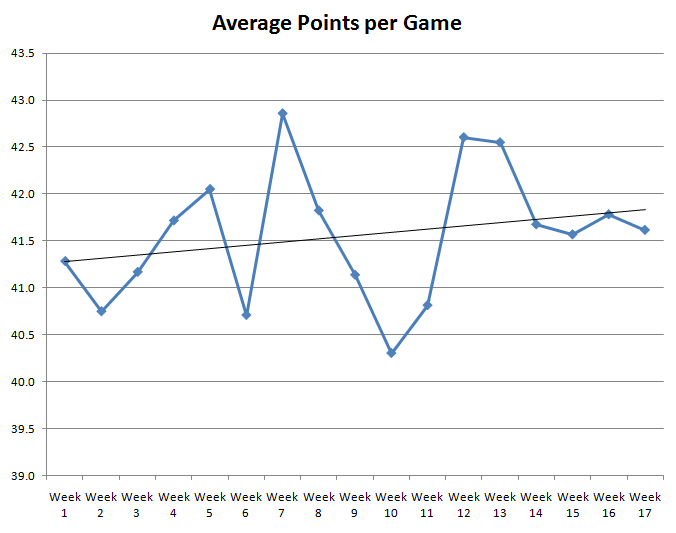
ご覧の通り、線は大きく上下しています。細い黒線は最小二乗法による最適近似線で、全体的に上昇傾向を示しています。季節が進み気温が下がると、平均得点はわずかに上昇しますが、これはランダムな変動である可能性も十分にあります。
私の理解できる範囲はこれくらいです。天候がスポーツベッティング全般にどのような影響を与えるかについて、一般的な意見を伺うため、この分野の専門家である友人のジェイソン・ビーンに話を聞きました。彼の意見は次のとおりです。
ほとんどの場合、試合に最も影響を与える天候の要素は風ですが、風だけが要因ではありません。野球やその他の屋外スポーツでは、特にシーズン序盤および終盤の午後の野球の試合では、影も同様に影響を与えることがあります。雨や雪は、フットボールでは多くの人が考えるほど大きな要因ではありません。一般的に、攻撃と守備の両方に等しく影響を与えるからです。一例として、ディフェンスバックとワイドレシーバーが挙げられます。雨と雪はどちらも同様にスピードを低下させるため、どちらの側にも優位性を与えません。フットボールでは、風によってパスゲームとキックゲームが簡単に消滅することがあります。パスチームが強い横風のためにほぼすべてのプレーでランを強いられた試合を見たことがあります。めったに起こりませんが、風が試合の最終的な勝敗を分けることもあります。この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
クラップスでプレイヤーがオッズ倍数を超えて賭け、ディーラーが賭けが勝つか負けるまでそれに気づかない場合、通常は何が起きますか?
元ベガスのテーブルゲームマネージャーにこの件について尋ねたところ、ラインベットの許容倍数を超えたオッズベットの部分は、プレースベットのオッズで支払われるとのことでした。この質問は、私の関連サイト「Wizard of Vegas」のフォーラムで提起され、議論されました。
NFL では、平均して、得点後に他のチームが次に得点する確率はどれくらいですか?
2000~2009 年の NFL シーズンに基づくと、答えは 57% です。
A、B、Cの3人が女性をめぐって死闘を繰り広げるトゥルエル(三者決闘)を考えてみましょう。彼らは全員紳士であり、以下のルールに同意しています。
- 3 人の参加者は三角形を形成します。
- それぞれ弾丸は1つだけです。
- 最初にA、次にB、そしてCが続きます。
- A が意図したターゲットに命中する確率は 10% です。
- B が意図したターゲットに命中する確率は 60% です。
- C が意図したターゲットに命中する確率は 90% です。
- 偶発的な発砲はありません。
- 空中での射撃(故意のミス)および自分自身の射撃は許可されており、常に成功します。
- どのラウンドでも2、3人の生存者が残っている場合、それぞれに新しい弾丸が与えられます。その後、同じ順番で交代で射撃を繰り返し、既に死亡した者を飛ばします。
- 参加者 3 人は全員完璧な論理学者です。
Aは最初に誰を狙うべきでしょうか?それぞれの初期ターゲットに対する彼の生存確率はどれくらいでしょうか?
このパズルはBBCの番組「Quite Interesting」で取り上げられています。答えと解答は100行下までスクロールしてください。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
それぞれの初期目標に応じて、Aが勝利する確率を以下に示します。ご覧のとおり、Aの勝利確率は意図的に空中に向けて発砲することで最大化されます。
トゥルーエルオッズ
| 戦略 | おそらく勝利 |
| 空気 | 13.887% |
| あ | 0.000% |
| B | 12.560% |
| C | 13.094% |
解答として、あるラウンドの後にグループXだけが残る確率をPr(X)と表記します。また、誰かが攻撃を受けてゲームの状態が変化するまで繰り返した後、グループXが最終的にラウンドに勝利する確率をPr(X*)と表記します。プレイヤーXが唯一の生存者となる確率をPr(X**)とします。最終的な確率を求めるために、まず2人のプレイヤーの状態を見てみましょう。それぞれが相手を撃つことは明らかです。
A対B
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
両者とも生き残った場合、生き残りが1人になるまでこの繰り返しが行われます。つまり、最後の生き残りとなる確率は以下のとおりです。
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375
A対C
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
両者とも生き残った場合、生き残りが1人になるまでこの繰り返しが行われます。つまり、最後の生き残りとなる確率は以下のとおりです。
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989
B対C
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
両者とも生き残った場合、生き残りが1人になるまでこの繰り返しが行われます。つまり、最後の生き残りとなる確率は以下のとおりです。
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375
3人プレイの場合を分析する準備ができました。AがBを狙っている状況を考えてみましょう。
3人プレイ — AがBを狙う
AがBを攻撃した場合、Cは確実に生き残りますが、Aを攻撃するかどうかはわかりません。つまり、Bを攻撃した場合の2つの可能な結果はACとCです。AがBを攻撃しなかった場合、Bはより脅威となるCを狙います。BがCを攻撃した場合、AとBは生き残ります。BがCを攻撃しなかった場合、Cはより脅威となるBを狙います。CがBを攻撃しなかった場合、3人とも生き残ります。CがBを攻撃した場合、AとCは生き残ります。つまり、可能な結果はC、AB、AC、ABCです。
- Pr(A) = 0です。
- Pr(B) = 0です。
- Pr(C) = 0.1 × 0.9 = 0.09。これは、AがBに衝突し、次にCがAに衝突することで達成されます。
- Pr(AB) = 0.9 × 0.6 = 0.54。これは、AがBをミスし、その後BがCをヒットすることで達成されます。
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334。これは2つの方法で達成できます。1つ目は、AがBに当たり、その後CがAをミスすることです。2つ目は、AがBをミスし、BがCをミスし、その後CがBに当たることです。
- Pr(BC) = 0です。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。これは3つすべてが欠けている状態で達成されます。
2 人のプレイヤーの場合と同じ論理で、ラウンド後にゲームの状態が変化したと仮定して、各結果を (1-Pr(ABC))=0.964 で割って、各状態の確率を見つけることができます。
- Pr(C*) = 0.09/0.964 = 0.093361。
- Pr(AB*) = 0.54/0.964 = 0.560166。
- Pr(AC*) = 0.334/0.964 = 0.346473。
2人プレイの場合、AとBの2人プレイではAが0.15625の確率で勝ち、Bが0.84375の確率で勝つことがわかります。AとCの2人プレイではAが0.109890の確率で勝ち、Cが0.890110の確率で勝つことになります。
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600。Aが勝者になるには2つの方法があります。(1) AB状態に到達してから勝利する、または(2) AC状態に到達してから勝利する。
- Pr(B**) = 0.560166 × 0.84375 = 0.472640。BがAB状態に到達し、その後Bが勝利すればBが勝者となる。
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760。Cが勝つには、AがBを倒し、その後Cが第1ラウンドでAを倒すか、または状態ACに到達し、その後Cが勝利する必要があります。
したがって、A の戦略が最初に B を狙うことである場合、彼が唯一生き残る確率は 12.56% です。
3人プレイ — AがCを狙う
AがCを攻撃した場合、Bは確実に生き残りますが、Aを攻撃するかどうかはわかりません。つまり、Cを攻撃した場合の2つの可能な結果はABとBです。AがCを外した場合、Bはより脅威となるCを狙います。BがCを攻撃した場合、AとBは生き残ります。BがCを外した場合、Cはより脅威となるBを狙います。CがBを外した場合、3つすべてが生き残ります。CがBを攻撃した場合、AとCは生き残ります。つまり、可能な結果はB、AB、AC、ABCです。
- Pr(A) = 0です。
- Pr(B) = 0.1 × 0.6 = 0.06です。
- Pr(C) = 0です。
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04 + 0.54 = 0.58。これは2つの方法で実現できます。1 つ目は、A が C にヒットし、その後 B が A をミスした場合です。2 つ目は、A が B をミスし、その後 B が C にヒットした場合です。
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324。これは、AがCをミスし、BがCをミスし、CがBにヒットすることで達成されます。
- Pr(BC) = 0です。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。これは3つすべてが欠けている状態で達成されます。
2 人のプレイヤーの場合と同じ論理で、ラウンド後にゲームの状態が変化したと仮定して、各結果を (1-Pr(ABC))=0.964 で割って、各状態の確率を見つけることができます。
- Pr(B*) = 0.06/0.964 = 0.062241。
- Pr(AB*) = 0.58/0.964 = 0.601660。
- Pr(AC*) = 0.324/0.964 = 0.336100。
A が B を目的とするケースの解決策と同じ論理により、
- Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943。
- Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891。
- Pr(C**) = 0.336100 × 0.890110 = 0.299166。
したがって、A の戦略が最初に C を狙うことである場合、彼が唯一生き残る確率は 13.09% です。
3人プレーヤー — Aが故意にミス
Aが故意にミスをした後、Bはより大きな脅威であるCを狙います。BがCを命中させれば、AとBは生き残ります。BがCをミスした場合、Cはより大きな脅威であるBを狙います。CがBをミスした場合、3人とも生き残ります。CがBを命中させれば、AとCは生き残ります。つまり、起こり得る結果はAB、AC、ABCです。
- Pr(A) = 0です。
- Pr(B) = 0です。
- Pr(C) = 0です。
- Pr(AB) = 0.6。これはBがCを打つことで達成される。
- Pr(AC) = 0.4 × 0.9 = 0.36。これは、BがCをミスし、その後CがBをヒットすることで達成されます。
- Pr(BC) = 0です。
- Pr(ABC) = 0.4 × 0.1 = 0.04。これは3つすべてが欠けている状態で達成されます。
2 人のプレイヤーの場合と同じ論理で、ラウンド後にゲームの状態が変化したと仮定して、各結果を (1-Pr(ABC))=0.96 で割って、各状態の確率を見つけることができます。
- Pr(AB*) = 0.6/0.96 = 0.625です。
- Pr(AC*) = 0.36/0.96 = 0.375。
A が B を目的とするケースの解決策と同じ論理により、
- Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865。
- Pr(B**) = 0.625 × 0.84375 = 0.527344。
- Pr(C**) = 0.375 × 0.890110 = 0.333791。
したがって、A の戦略が最初に C を狙うことである場合、彼が唯一生き残る確率は 13.89% です。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。


