Wizardに尋ねる #270
ペアを無制限にスプリットできるカジノでプレイしています。このルールはどのような影響がありますか?
最大4ハンドまでのスプリットと比較した場合、無制限の再スプリットの価値は、ルールがエースを含むすべてのペアに適用される場合0.05%、エースを含まない場合は0.02%であることを示します。この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
どうやらLVHは、VCUが全米選手権で優勝するチケットを10ドルで5000倍で販売しているようです。VCUが優勝すれば5万ドルの配当となります。もしあなたがこのチケットを持っているとしたら、現時点で交換に応じられる最低金額はいくらですか?(明日からファイナル4が始まります)
PinnacleでVCUの優勝予想ラインは、以下のようになっています。はい +604 いいえ -750 どちらに賭けてもVCUの優勝が確定するには、VCUの優勝にどれだけ賭けるべきか、そしてその勝利額はいくらになるか計算してみましょう。賭け金はxとします。勝利額 = 50,000 - x
負けた場合の結果 = x*(100/750) = (2/15)x これを等しくすると、50000-x = (2/15)x 50000 = (17/15)xx = 50000×(15/17) x = $44,117.65 となります。これが正しいかどうか確認してみましょう。VCUが勝った場合、$50,000からヒルトンからの配当$44,117.65を差し引いた$5,882.35がPinnacleに支払われます。VCUが勝てなかった場合、Hiltonからは何も得られませんが、Pinnacleは$44,117.65 × (100/750) = $5,882.35を支払います。しかし、VCUに賭けた場合、公平なオッズが支払われるとは思えません。もしオーナーが極めてリスク回避的で、チケットを早く売りたがっていたとしたら、6,000ドル程度が妥当な価格だと思います。しかし、VCUの勝率は+604ラインを基準にすると、100/704 = 14.2%の確率となります。そうすると、チケットの価値は約7,100ドルになります。これは税金の影響を考慮していない計算です。この疑問は、私の関連サイト 「Wizard of Vegas」のフォーラムで提起され、議論されました。
パイゴウポーカーでバンキングしない場合に得られる最高のハンドは何ですか?
バンキングをしていない限り、絶対に負けないハンドは存在しないようです。そこで、2つのハンドを考えてみましょう。1つ目はハイで負けたり、引き分けたりすることはありません。2つ目はローで負けたり、引き分けたりすることはありません。
(1) AAAAW/KK (W=ワイルド)
5枚のエースはハイでは負けませんが、キングのペアはローでタイになる可能性があります。2枚のキングの組み合わせの数は、 combin (44,5) = 1,086,008です。残りの46枚のうち7枚のカードの組み合わせの合計数は53,524,680です。したがって、2枚のキングの確率は1,086,008/53,524,680 = 2.03%です。これらの組み合わせの多くでは、ディーラーはローでKKをプレイしません。私のパイゴウポーカー付録1によると、ディーラーはハイでエースのペア以下を持っている確率は74.93%です。つまり、ディーラーはツーペア以上になり、ローでキングをプレイできる確率は25.07%です。したがって、プレイヤーが 2 つのキングを取得し、それをローでプレイできる確率は、2.03% × 25.07% = 0.51%、つまり 196 分の 1 になります。
(2) AWQJT(スーツ)/AA
ロイヤルはハイでタイになることがありますが、エースはローで負けたりタイになったりすることはできません。ここでは、ワイルドをキングの代わりに使用してロイヤルを作成していますが、Q、J、またはTの代わりに使用することもできます。エースの代わりにすることは望ましくありません。そうしないと、ディーラーがローをタイできるようにデッキに2つのエースが残ってしまうためです。この方法では、ディーラーはハイを別のロイヤルとしかタイにできません。その確率はどれくらいでしょうか? ロイヤルには3つのスーツが残っており、他の2枚のカードは何でもかまいません。したがって、プッシュする組み合わせの数は、3×combin(41,2) = 2,460です。プレーヤーが元の43から7を取り除いた後にデッキに残っている46枚のカードから41を取得し、ディーラーのロイヤルの5枚のカードのためにさらに5を引きます。分母はcombin(46,7) = 53,524,680です。したがって、ワイルド ロイヤル/AA との引き分けのオッズは 2,460/53,524,680 = 0.004596%、つまり 21,758 分の 1 となります。
完璧主義者の誰かが私にメールをくれる前に、ディーラーが私の意図通りにプレイしてくれないという奇妙な状況がいくつかあるかもしれないことをお伝えしておきます。それぞれの状況の正確な確率を求めているのではなく、パイゴウポーカーでバンキングをしていないときにワイルドロイヤル/AAが最高のハンドだと考える理由を裏付けたいのです。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
一卵性双生児以外の兄弟姉妹と共通する遺伝子の比率はどのくらいでしょうか?
1/2。
キノに例えると、誰もが40個の遺伝子を持ち、それぞれがキノのボールで表現されます。ただし、それぞれのボールには固有の番号が振られています。血縁関係のない二人が交配すると、それは二人で80個のボールをホッパーに集め、交配によって生まれた子孫のために40個の遺伝子をランダムに選択するようなものです。
つまり、あなたが受胎した時、あなたはホッパーに入っていたボールの半分を受け取り、残りの半分は無駄になりました。あなたの兄弟姉妹が受胎した時、彼または彼女はあなたが生まれた時に抽選されたボールの半分を受け取り、残りの半分は抽選されなかったボールを受け取りました。つまり、あなたは遺伝的に50%同一です。これは、キノで40個の数字が抽選された場合、2回連続して抽選されると平均20個のボールが共通するのと同じ理由です。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
テーブルと椅子を生産する工場には、のこぎり10台、旋盤6台、研磨機18台が備え付けられています。椅子1脚の製作には、のこぎりで10分、旋盤で5分、研磨で5分かかります。テーブル1脚の製作には、のこぎりで5分、旋盤で5分、研磨で20分かかります。椅子の販売価格は10ドル、テーブルの販売価格は20ドルです。工場が1時間あたりにテーブルと椅子を何脚生産すれば、最大の収益が得られるでしょうか?また、その収益はいくらでしょうか?
1時間あたりに製造される椅子の数をc、テーブルの数をtとすると、1時間あたりの収益は10×c + 20×tとなります。
10台ののこぎりで1時間あたり600分の鋸引き作業が必要になります。椅子の場合は鋸引きに10分、テーブルの場合は5分かかると仮定すると、1時間あたりの生産量は以下のようになります。
(1)10セント+5トン<=600
旋盤6台で1時間あたり360分の旋盤加工が可能です。椅子は鋸で5分、テーブルは5分かかると仮定すると、1時間あたりの生産量は以下のようになります。
(2)5c + 5t <= 360
18台のサンディングマシンで1時間あたり1080分のサンディング作業が行われます。椅子の場合は鋸で5分、テーブルの場合は20分かかると仮定すると、1時間あたりの生産量は以下のようになります。
(3)5c + 20t <= 1080
次のグラフは、3組の機械によって課される3つの制約を示しています。工場は、3本の線すべてに該当する椅子とテーブルの組み合わせを自由に生産できます。問題は、3本の線のうちどの線に該当する場合、収益が最大になるかということです。
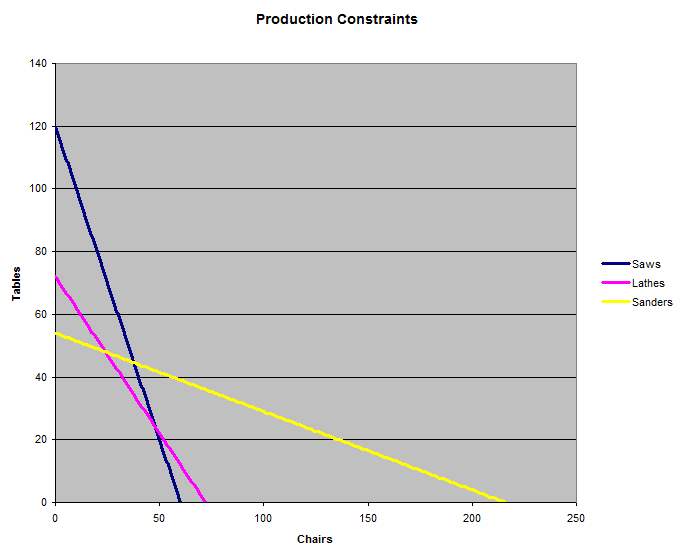
答えは当然、2本の直線の交点、椅子を全て作るか、テーブルを全て作るかのいずれかになるでしょう。では、直線が交差する場所を見つけましょう。まず、式(1)と(2)が交差する場所を見つけましょう。機械の能力を最大限に引き出すために、<= という式を = に置き換えることができます。
(1)10セント+5トン=600
(2)5c + 5t = 360
(1)から(2)を引く:
5セント = 240
c = 48
式(1)にcの48を代入すると、
10×48 + 5t = 600
5t = 120
t = 24
したがって、式(1)と式(2)は椅子48脚とテーブル24台のところで成り立ちます。
次に、式(2)と式(3)が交わる場所を見つけましょう。
(2)5c + 5t = 360
(3)5セント+20トン=1080
(3)から(2)を引くと、
15トン = 720
t = 48
これを(2)または(3)に代入するとcを解くことができ、それは24です。
したがって、式(2)と式(3)は椅子24脚とテーブル48台のところで成り立ちます。
グラフから鋸とサンダーの線が交わるところが旋盤の制約の外側にあることがわかるので、方程式(1)と(3)が交わるところを探す必要はありません。
椅子だけを作るのが正解である可能性もあります。グラフからわかるように、椅子だけを作る場合、鋸が最大の制約となります。式(1)から、テーブルの数を0とすると、c=60となります。
もう一つの可能性は、テーブルだけを作ることです。グラフから、サンダーが最大の制約となることがわかります。式(3)に椅子を0脚と代入すると、テーブルは54台しか作れないことがわかります。
次のグラフは、それぞれの有効な回答に対する総収益を示しています。収益は椅子1脚あたり10ドル、テーブル1台あたり20ドルです。
総時間収入
| 椅子 | テーブル | 収益 |
| 0 | 54 | 1,080ドル |
| 24 | 48 | 1,200ドル |
| 48 | 24 | 960ドル |
| 60 | 0 | 600ドル |


