Wizardに尋ねる #284
シアトルの自動車販売店が、シーホークスがジャイアンツを完封したせいで42万ドルを支払わなければならなかったという話を聞きましたか？ 保険に7,000ドル支払わなければならなかったと読んだのですが、妥当な保険料はいくらだったのでしょうか？
「ワシントンの自動車販売店、シーホークス完封後に42万ドルを支払う」という記事によると、この販売店は、2013年12月15日に行われた第15週の試合でシーホークスがジャイアンツを完封した場合、12人の勝者にそれぞれ3万5千ドルを支払うというプロモーションを実施していた。記事にはさらに、販売店は、実際にそのような事態になった場合に備えて、保険に7千ドルを支払ったと書かれている。
1983年から2012年までのNFLの全試合を振り返ると、どの試合でも特定のチームがシャットアウトされています。しかし、7点差のアンダードッグとして、平均的なオーバー/アンダーの試合でジャイアンツがシャットアウトされる確率は平均よりも高かったと私は考えます。この試合のオーバー/アンダーは41でした。少し代数を使って、ジャイアンツの予想得点数を計算してみましょう。
させて：
s=シーホークスの得点
g=ジャイアンツポイント
ポイントスプレッドとオーバー/アンダー合計に基づくと、s+g=41、s=g+7 であることがわかります。
2 番目の方程式を 1 番目の方程式に代入します。
（g+7）+g = 41
2g + 7 = 41
2g = 34
グラム = 17
次に、1983年から2012年のシーズンに基づいて、各チームの推定得点数から完封確率を見てみましょう。サンプル数が0の行は省略しました。
次のステップはここで説明するには複雑すぎるが、推定ポイント数に基づいて完封の確率を計算する式を開発しました。
p = 推定ポイント。
x = 1.562545 -0.302485 * p
完封確率 = e x /(1+e x )
次のグラフは、14 ～ 22 ポイントでの完封の実際および推定確率を示しています。
問題の試合ではジャイアンツは17点を獲得すると予想していた。
表の上の式を使用します。
x = 1.562545 -0.302485 * 17 = -3.579706
完封確率 = exp(-3.579706)/( exp(-3.579706)+1) = 2.71%。正確には0.0271275。
ジャイアンツが完封負けした場合、ディーラーは42万ドルを支払わなければならなかったことを考えると、保険料は42万ドル × 0.0271275 = 11,394ドルとなるはずです。通常、このような異例のプロモーションを実施する保険会社は、保険料を2倍に引き上げるので、保険料は22,788ドルになるはずでした。つまり、ディーラーが支払った7,000ドルという保険料は、まさに破格の値段だったのです。仮に社長が計算を見直したとしても、7,000ドルという保険料を計算した人の立場にはなりたくないですね。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。
1983年から2012年までのNFLの全試合を振り返ると、どの試合でも特定のチームがシャットアウトされています。しかし、7点差のアンダードッグとして、平均的なオーバー/アンダーの試合でジャイアンツがシャットアウトされる確率は平均よりも高かったと私は考えます。この試合のオーバー/アンダーは41でした。少し代数を使って、ジャイアンツの予想得点数を計算してみましょう。
させて：
s=シーホークスの得点
g=ジャイアンツポイント
ポイントスプレッドとオーバー/アンダー合計に基づくと、s+g=41、s=g+7 であることがわかります。
2 番目の方程式を 1 番目の方程式に代入します。
（g+7）+g = 41
2g + 7 = 41
2g = 34
グラム = 17
次に、1983年から2012年のシーズンに基づいて、各チームの推定得点数から完封確率を見てみましょう。サンプル数が0の行は省略しました。
完封確率
| 推定 ポイント | サンプルサイズ | 完封 | 比率 |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11時00分 | 13 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12時 | 34 | 2 | 5.9% |
| 12.25 | 36 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 39 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16時 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18時 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21時 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 48 | 0 | 0.0% |
| 29.25 | 34 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 25 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
次のステップはここで説明するには複雑すぎるが、推定ポイント数に基づいて完封の確率を計算する式を開発しました。
p = 推定ポイント。
x = 1.562545 -0.302485 * p
完封確率 = e x /(1+e x )
次のグラフは、14 ～ 22 ポイントでの完封の実際および推定確率を示しています。
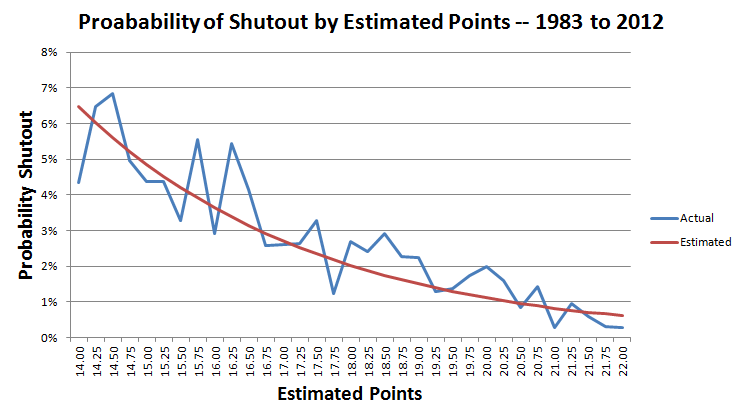
問題の試合ではジャイアンツは17点を獲得すると予想していた。
表の上の式を使用します。
x = 1.562545 -0.302485 * 17 = -3.579706
完封確率 = exp(-3.579706)/( exp(-3.579706)+1) = 2.71%。正確には0.0271275。
ジャイアンツが完封負けした場合、ディーラーは42万ドルを支払わなければならなかったことを考えると、保険料は42万ドル × 0.0271275 = 11,394ドルとなるはずです。通常、このような異例のプロモーションを実施する保険会社は、保険料を2倍に引き上げるので、保険料は22,788ドルになるはずでした。つまり、ディーラーが支払った7,000ドルという保険料は、まさに破格の値段だったのです。仮に社長が計算を見直したとしても、7,000ドルという保険料を計算した人の立場にはなりたくないですね。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。
最大の素数が存在しないという証明は何ですか?
少しの間、最大の素数があると仮定しましょう。素数をp1=2、p2=3、p3=5、p4=7、…と番号付けすると、pL = 最大の素数となります。
ここで、数値 x = p1*p2*p3*p4*...*pL + 1 を定義します。
素数であるということは、他のどのより小さい素数もそれを割り切れないことを意味します。
p1、p2、p3、... pL を x で割ると、毎回余りが 1 になります。
pLよりも大きな素数はxを割り切れるかもしれない、と主張するかもしれません。確かにその通りですが、その場合、いわゆる最大素数よりも大きな素数を見つけたことになります。そうでなければ、xは新たな最大素数となり、最大素数の存在という当初の予想は背理法によって証明されます。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されました。
Business Insider の「数学的に言うと、メガミリオンズのチケットを今すぐ買うべき」という記事に同意しますか?
いいえ、同意しません。これはひどいジャーナリズムであり、Business Insiderは恥じるべきです。
まず、この記事は2013年12月17日、つまりその夜に行われた6億3600万ドルの抽選の前に公開されました。1ドルのチケットの価値を評価するための計算を見てみましょう。以下の表は、6億3600万ドルのジャックポットのあらゆる可能性について、一括払いペナルティ、税金、ジャックポットの分配といった要素を考慮する前の確率と期待収益を示しています。上位3つの確率は、数値が非常に小さいため、科学的記数法で表示されています。
メガミリオンズ -- 6億3600万ドルのジャックポット
| キャッチ | メガボール | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|---|
| 5 | はい | 6億3,600万ドル | 1 | 3.86E-09 | 2.456634 |
| 5 | いいえ | 100万ドル | 14 | 5.41E-08 | 0.054077 |
| 4 | はい | 5,000ドル | 350 | 1.35E-06 | 0.006760 |
| 4 | いいえ | 500ドル | 4,900 | 0.000019 | 0.009463 |
| 3 | はい | 50ドル | 24,150 | 0.000093 | 0.004664 |
| 3 | いいえ | 5ドル | 338,100 | 0.001306 | 0.006530 |
| 2 | はい | 5ドル | 547,400 | 0.002114 | 0.010572 |
| 1 | はい | 2ドル | 4,584,475 | 0.017708 | 0.035416 |
| 0 | はい | 1ドル | 12,103,014 | 0.046749 | 0.046749 |
| 敗者 | 0ドル | 2億4128万8446円 | 0.932008 | 0.000000 | |
| 合計 | 2億5,889万850 | 1.000000 | 2.630865 | ||
つまり、1ドルのチケットは2.630864ドルの利益になります。チケット代金を差し引くと、期待利益は1.630864ドルになります。Business Insiderは1.632029ドルの利益を得ます。0.001164ドルの差ですが、大した問題ではありません。
ただし、価値を大幅に下げる 3 つの要素があります。
- 一時金の罰金。
- 税金。
- ジャックポットの分配。
一つずつ見ていきましょう。
メガミリオンズを含め、高額宝くじのプログレッシブ・ジャックポットは通常、約30年間の年金形式で支払われます。当選者が一度に賞金を受け取りたい場合（ほとんどの当選者はそうでしょう）、大幅な減額を受けなければなりません。今日の1ドルは将来の1ドルよりも価値があるため、これは当然のことです。2013年12月17日の抽選では、賞金総額は3億4,760万ドル、つまり宣伝されていたジャックポットの54.65%に減額されました。
次に税金について見てみましょう。連邦所得税の最高限界税率は39.6%です。州税は0%から12.3%の範囲なので、平均6%としましょう。税金の45.6%を差し引くと、1億8,910万ドルが残ります。
ここからが最も難しい部分、つまりジャックポットの分配です。2013年10月22日の抽選から、メガミリオンズの抽選ルールは75-15形式に変更されました。つまり、1から75までの数字を5つ選び、次に1から15までの別のプールから1つ選びます。これにより当選確率は2億5889万850分の1に下がりましたが、これは明らかにジャックポットを大きくするためです。それ以降の17回の抽選だけを見て、 LottoReport.comのジャックポットと売上データを使用したところ、ジャックポットのサイズと需要の間には指数関係があることがわかりました。ちなみに、パワーボール宝くじでも同じことがわかりました。指数回帰を使用して、販売されたチケットの合計数（百万枚）を求める式は12.422 × exp(0.0052 × j)です。ここで、jはジャックポットのサイズ（百万枚）です。例えば、6億3,600万ドルのジャックポットの場合、予想売上高は12.422 * exp(0.0052*636) = 3億3,920万ドルとなります。実際の売上高は3億3,700万ドルだったので、ほぼ予想通りです。
実際のチケット販売枚数336,545,306枚に基づくと、336,545,306/258,890,850 = 1,300人の当選者が予想されます。ここで重要な疑問は、当選した場合、賞金を何人分け合えるかということです。これはポアソン分布を見れば簡単に答えられます。当選者の平均数が1.3人の場合、当選者がちょうどx人になる確率はexp(1.3)×1.3 x / fact(x)です。次の表は、当選者が0人から10人になる確率、それぞれの場合の当選者への配当、そして当選した場合の予想配当を示しています。
平均1.3人の当選者に与えられるジャックポットの予想シェア
| その他の受賞者 | 確率 | ジャックポットシェア | 予想シェア |
|---|---|---|---|
| 10 | 0.000001 | 0.090909 | 0.000000 |
| 9 | 0.000008 | 0.100000 | 0.000001 |
| 8 | 0.000055 | 0.111111 | 0.000006 |
| 7 | 0.000339 | 0.125000 | 0.000042 |
| 6 | 0.001827 | 0.142857 | 0.000261 |
| 5 | 0.008431 | 0.166667 | 0.001405 |
| 4 | 0.032429 | 0.200000 | 0.006486 |
| 3 | 0.099786 | 0.250000 | 0.024946 |
| 2 | 0.230283 | 0.333333 | 0.076761 |
| 1 | 0.354295 | 0.500000 | 0.177148 |
| 0 | 0.272545 | 1.000000 | 0.272545 |
| 合計 | 1.000000 | 0.559602 |
右下のセルには、賞金の 55.96% をあなたが保持でき、残りの 44.04% は他の当選者と分け合わなければならないことが示されています。
これで、6億3,600万ドルのジャックポットは、1億8,910万ドル × 55.96% = 1億580万ドルに減りました。この金額をジャックポットとした場合の払い戻し表を見てみましょう。
メガミリオンズ -- 1億580万ドルのジャックポット
| キャッチ | メガボール | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|---|
| 5 | はい | 1億580万ドル | 1 | 3.86E-09 | 0.408666 |
| 5 | いいえ | 100万ドル | 14 | 5.41E-08 | 0.054077 |
| 4 | はい | 5,000ドル | 350 | 1.35E-06 | 0.006760 |
| 4 | いいえ | 500ドル | 4,900 | 0.000019 | 0.009463 |
| 3 | はい | 50ドル | 24,150 | 0.000093 | 0.004664 |
| 3 | いいえ | 5ドル | 338,100 | 0.001306 | 0.006530 |
| 2 | はい | 5ドル | 547,400 | 0.002114 | 0.010572 |
| 1 | はい | 2ドル | 4,584,475 | 0.017708 | 0.035416 |
| 0 | はい | 1ドル | 12,103,014 | 0.046749 | 0.046749 |
| 敗者 | 0ドル | 2億4128万8446円 | 0.932008 | 0.000000 | |
| 合計 | 2億5,889万850 | 1.000000 | 0.582898 | ||
右下のセルには、期待収益率が58.29%と表示されています。つまり、1ドルの投資で約58セントの利益が期待でき、期待損失、つまりハウスエッジは約42%になります。これは、チケットを買うべきという計算に聞こえますか？
記事によると、「したがって、現時点ではかなりありそうな状況ですが、販売されたチケットが 7 億 3000 万枚未満である限り、チケットの期待値はプラスになるはずなので、今日メガ ミリオンズのチケットを購入することを検討すべきです。」
売上高は7億3000万台よりはるかに少なかったものの、それでもひどい金額でした。しかし、公平を期すために、記事には次のように書かれていました。
この分析には多くの注意点があることに留意してください。税金は、予想される利益にかなり大きな打撃を与える可能性があります。連邦政府は約40%を徴収し、居住州は0%から約13%を請求します。
多くの人がチケットを購入しており、前述の通り、これにより引き分けの確率が大幅に高まり、それに伴う配当も減少するだろう」— Business Insider
これらはかなり重要な注意事項です！最後に軽く触れるだけでなく、分析の最初から考慮に入れるべきです。
質問されたわけではないのですが、計算上はメガミリオンズには絶対に手を出すべきではないと思います。ジャックポットの額から判断すると、チケットの需要が指数関数的に増加していることを考えると、5億4500万ドルのジャックポットが当たる時が最適なタイミングだと私は考えています。それ以上の額になると、他の当選者と分け合わなければならなくなります。その額のジャックポットでは、プレイヤーは60.2%の払い戻し、つまり39.8%の損失を期待できます。これ以上の額は考えられません。
最後に、Business Insider がセンセーショナルなタイトルで読者を騙し、税金やジャックポットの分配について適切な分析を行っていないことには、私は同意しません。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。