Wizardに尋ねる #301
地元のカジノでは毎週抽選が行われ、当選者には 5,000 ドルの現金、または以下のいずれかの賞品が入ったミステリー バッグを選ぶオプションが提供されます。
- 現金2,000ドル
- 4,000ドルの交渉不可チップ
- 6,000ドルの交渉不可チップ
- 現金8,000ドル
- 現金1万ドル
あなたなら何を選びますか、そしてその理由は何ですか?
まず、「譲渡不可チップ」とは、負けるまで使えるタイプのチップだと思います。これらのチップの価値は、使用できるゲームのルールにもよりますが、額面の約98%です。
とはいえ、平均的なバッグの価値は5,960ドルです。これは現金で提示される金額より約20%高い金額です。お金の効用という観点から見ても、他に財産がなくてもバッグは受け取るべきです。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されました。
合計が 1 になるには、0 から 1 までの一様分布から平均何回抽出する必要があるでしょうか。
映画『グッド・ウィル・ハンティング』の黒板に書かれていた数学の問題は何でしたか?
MITの組み合わせ数学の授業にしては、実はかなり簡単でした。問題の文言は次のとおりです。
「サイズ n=10 の同相的に既約な木をすべて描画します。」
これを平易な英語で説明してみることにします。
直線のみを使って、交差点と行き止まりの合計が10となる図形をすべて描きます。閉じたループはあってはなりません。また、2つの同値な図形があってはなりません。交差点からは、少なくとも3本の線が伸びている必要があります。
「同等」とはどういう意味でしょうか? 交点をそのままにして、ピースを好きなように動かしても、新しい図形は作成されないという意味です。
次に例を示します。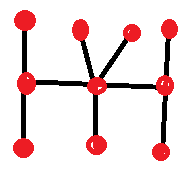
ヒントをあげましょう。映画の答えとは違い、答えは10個あります。ウィルは8個しか答えられませんでした。ウィル・ハンティングに匹敵するか、あるいはウィルを上回れるか、試してみてください。
[ネタバレ]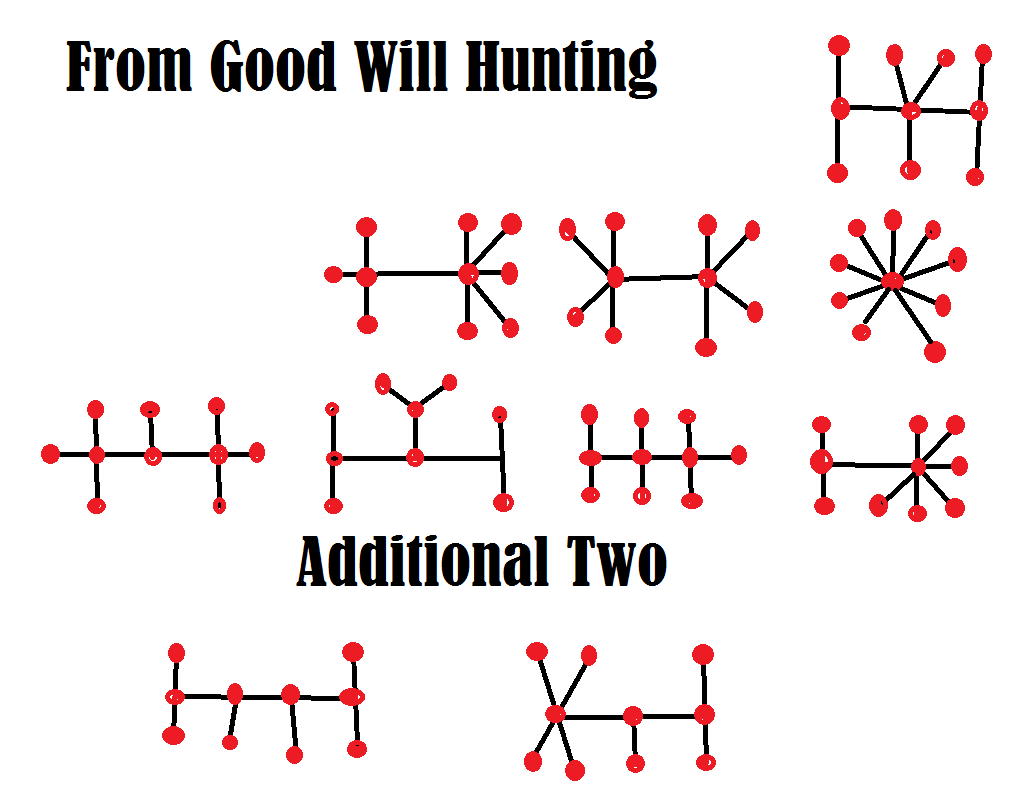
10 個すべてを導き出すための私の論理は、私のMathProblems.infoサイトの問題 220 で示されています。
[/spoiler] さらに読む:- 『グッド・ウィル・ハンティング II』における数学: 学生の観点から見た問題- 問題に関する学術論文。
- 『グッド・ウィル・ハンティング』の数学問題-- 私のフォーラムでこの問題について議論します。
メキシコの一部のカジノでは、ルーレットにホイールではなくサイコロが使われています。ルールは以下のとおりです。
- サイコロは 4 つあります。緑が 2 つ、赤が 1 つ、青が 1 つです。
- 2 つの緑のサイコロが両方とも 1 つに止まった場合、「スピン」の結果はゼロになります。
- 2 つの緑のサイコロが両方とも 6 になった場合、「スピン」の結果は 2 つのゼロになります。
- 緑のサイコロで他の結果が出た場合、赤と青のサイコロの 36 通りの結果が 1 と 36 の数字にマッピングされ、「スピン」を表します。
従来のルーレットと比べてオッズはどのように変化するのでしょうか?
0と00が当たる確率はそれぞれ1/36です。もしこれらの結果に賭けた場合、通常の35倍の配当が得られるとすれば、ハウスエッジはちょうど0%になります。
他の数字が当たる確率は(34/36)*(1/36) = 2.62%です。これを、従来のダブルゼロルーレットの1/38=2.63%と比較してみてください。1から36までの数字に賭けた場合のハウスエッジは5.56%です。これを、従来のダブルゼロルーレットの5.26%と比較してみてください。このゲームでは、ゼロとダブルゼロだけに賭けることをお勧めします。
これらのルールと支払いについて確認または否定できる方がいらっしゃいましたら、お知らせください。


