Wizardに尋ねる #322
テキサスホールデムのゲームに参加していたのですが、進行中のハンドでハイハンドがストレートフラッシュでした。テーブルの他の二人のプレイヤーが、3回連続のストレートフラッシュだと言っていました。その確率はどれくらいでしょうか?
10人のプレイヤーがテキサスホールデムをプレイする場合、誰もフォールドしないと仮定すると、ハイハンドがストレートまたはロイヤルフラッシュになる確率は350.14分の1です。3回中3回、この確率でストレートまたはロイヤルフラッシュになる確率は42,926,491分の1です。
しかし、そのテーブルは何時間もプレイされていたかもしれません。より現実的な質問は、1日のうち少なくとも1回はそのようなことが起こる確率はどれくらいか、ということです。24時間プレイし、1時間あたり24ハンドプレイすると仮定すると、その答えは59,621分の1になります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
適切な戦略を前提とした場合、アルティメット・テキサス・ホールデムで4倍のレイズを受けた場合の勝率はどれくらいでしょうか?4倍のハンドを96回記録しました。プッシュを除いて、66勝30敗でした。これは期待値と比べてどうでしょうか?
正しい 4 倍のレイズ戦略を前提とすると、4 倍のレイズが与えられた場合の各結果の確率は次のようになります。
- 勝率: 58.82%
- 損失: 38.47%
- 同率: 2.72%
引き分けを除くと、勝利確率は60.46%です。96ハンドの結果で、4倍の勝利の期待値は58.04です。つまり、66回の勝利は予想を上回っていますが、それほど大きな差ではありません。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
アクセルとボブはそれぞれ52枚のカードのデッキを持っています。二人ともデッキをランダムにシャッフルします。そして、それぞれのデッキから同時に1枚ずつカードをめくります。二人が同じカードを少なくとも1回同時にめくる確率はどれくらいでしょうか?
答えを1-(51/52) 52 = 0.63568648と簡単に推定できます。しかし、推定だけでは知識として納得できません。では、正確な解を求めましょう!
ステップ 1: まず、最初のカードが 1 番である場合に 2 番目のデッキを並べる方法の数を考えます。答えは、他の 51 枚のカードを並べる方法の数で、51! = 15511187532873822802242430164693032110632597200169861120000000000000 です。
どのカードも最初のデッキと一致する可能性があるため、52枚すべてに対してこの手順を実行する必要があります。これにより、少なくとも1枚のカードが一致する組み合わせは52*51! = 52!通りになります。
ステップ2:ただし、ステップ1では、2枚のカードが一致するすべての状況を2倍にカウントします。例えば、最初の2枚のカードが1と2の場合、他のカードの配置方法は50!通りで、1枚目を最初のカードとして1回、2枚目を2枚目として2回、計2回カウントします。52枚の中から2枚のカードを選ぶ方法はcombin(52,2) = 1326通りです。2枚のカードの組み合わせごとに、他のカードを並べる方法は50! = 30414093201713378043612608166064768844377641568960512000000000000通りあります。したがって、ステップ2では、combin(52,2)*50! = (52*51/2!)*50! = 52!/2!通りの組み合わせを減算する必要があります。
ステップ 3: 次に、ランダム デッキの最初の 3 枚のカードが 1、2、3 の順に並んでいる状況を考えます。残りの 49 枚のカードを並べる方法は 49! 通りあります。少なくとも 1 枚の一致するカードを数える最初のステップで、それらを 3 回数えたことになります。次に、2 番目のステップで、これらの 3 枚のカードから 2 枚を選ぶ combin(3,2)=3 通りの方法をすべて差し引きます。つまり、この状況は 3-3=0 回数えられたことになるので、それらを再び追加する必要があります。少なくとも 3 枚の一致するカードを選ぶ状況は combin(52,3) 回あります。したがって、combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! 通りの組み合わせを再び追加する必要があります。
ステップ 4: 次に、ランダム デッキの最初の 4 枚のカードが 1、2、3、4 の順に並んでいる状況を考えます。残りの 48 枚のカードを並べる順序は 48! 通りあります。少なくとも 1 枚の一致するカードを数える最初のステップで、それらを 4 回数えます。次に、ステップ 2 でこれらの 4 枚のカードから 2 枚を選ぶ combin(4,2)=6 通りをすべて差し引きます。次に、これらの 4 枚のカードから 3 枚を選ぶ combin(4,3)=4 通りをすべて加算します。つまり、このような状況はそれぞれ 4-6+4=2 通り数えられます。したがって、これらの方法の 1 つを差し引いて、各状況が 1 回ずつ数えられるようにする必要があります。このような状況は、combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! 通りあります。
これを繰り返して、加算と減算を交互に繰り返し、重複カウントを修正します。
最終的に、ランダム デッキ内の少なくとも 1 枚のカードが順序付けられたデッキと一致する状況の数 = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783。
52 枚のカードを並べる方法は全部で 52! = y = 527177615496365219422618541545122659969212453861982208000000000000 通りあります。
したがって答えはx/y = 0.6321205588285576784044762298となる。
一致するものがない確率は、1-(x/y) = 0.3678794411714423215955237702 です。
この数字に見覚えがあるなら、その通りです。1/e = 0.3678794411714423215955237702。
したがって、答えは 1-(1/e) と非常に近い値と推定できます。
謝辞
数学的計算はPari/GPで行われた。
この問題は、Wizard of Vegasの私のフォーラムで質問され、議論されました。
あなたのサイトにある「ビンゴのパターン確率(PDF)」というタイトルの文書では、300 枚のカードがプレイされていると仮定して、勝者を見つけるために予想されるコール回数が次のようになっていると述べています。
- 四隅:8.43
- スモールダイヤモンド:11.833
どちらのパターンも必要なマークは4つだけで、勝ち方も1つだけです。なぜ、勝者を見つけるために必要なボールの期待値が異なるのでしょうか?
これは説明が難しい答えです。まず、1枚のカードを使ったゲームでは期待されるコール数は同じですが、複数のカードを使うと相関効果が現れるということを述べさせてください。
この質問に簡単に答えるのは難しいですが、強いて言えば、4コーナーパターンではB列とO列にボールが集中する必要があるからです。一方、スモールダイヤモンドパターンでは、B列、N列、O列にボールがフラットに分散している方が、ヒットする可能性が高くなります。
ゲームを単純化して、無限のカードが使われ、ボールが入れ替わりながら引かれるゲームを考えてみましょう。両方のゲームで勝者を出すために必要なボールの数は、以下の通りです。
- 4つのコーナー:2.5+2.5+((1/2)*10+(1/2)*(2.5+5)) = 13.75
- 小さなダイヤモンド: =(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
これは、4 つのコーナーに 1.53 個のボールが余分にかかることを示しています。
通常のビンゴ ルールで、カードが無限にあると仮定してシミュレーションを実行すると、次のようになります。
- 四隅: 12.8289
- ダイヤモンド: 11.3645
今回は1.46ボールの異なる。
私が示したいのは、マークが複数の列に分散しているほど、パターンがより早くカバーされる可能性が高くなるということです。そのため、シングルビンゴゲームでは、当選ビンゴは通常、横並びになると思います。
この質問はWizard of Vegasの私のフォーラムで尋ねられ、議論されています。
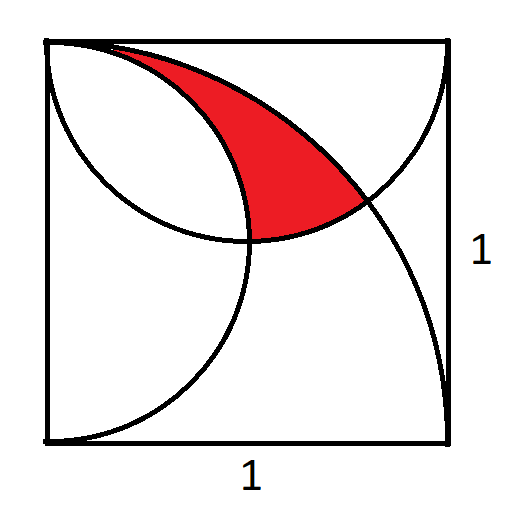
上の図では、辺の長さが1の正方形の中に四分の一円と半円が2つあります。赤い領域の面積はいくらでしょうか?
私の回答については次のボタンをクリックしてください。
私の解決策については次のボタンをクリックしてください。
ここに私の解決策へのリンクがあります。(PDF)
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
謝辞: この数学パズルを提供してくれたMind Your Decisionsに感謝します。


