Wizardに尋ねる #323
このパーレーカードは良いですか?

ステップ1では、NFLの試合でスプレッドに反してどちらかに賭ける必要があります。この質問をした時点(2020年1月2日)では、バイキングスは7.5ポイントのアンダードッグでした。私のNFL代替ポイントスプレッド計算機によると、バイキングス+8.5がそのサイドで勝つ確率は52.22%です。
その他の試合については、現在のマネーラインからジュースを差し引いて勝率を算出しました。以下の表は、各レグの勝率を示しています。
ウィリアムヒルパーレーカード
| 脚 | フェアワイン | おそらく勝利 |
|---|---|---|
| セインツ -8.5 | -7.5 | 47.78% |
| バイキング +8.5 | 8.5 | 52.22% |
| ホウ | -135 | 57.45% |
| 請求書 | 135 | 42.55% |
| ペイトリオッツ | -205 | 67.21% |
| タイタンズ | 205 | 32.79% |
| 海 | -118 | 54.13% |
| フィル | 118 | 45.87% |
| LSU | -200 | 66.67% |
| クレムソン | 200 | 33.33% |
| AFC | -130 | 56.52% |
| NFC | 130 | 43.48% |
ステップ1で勝利の可能性が高いのは、ペイトリオッツとLSUの2チームです。私が推奨するチームの勝利確率は以下の通りです。
- バイキング +8.5 — 52.22%
- ペイトリオッツ — 67.21%
- LSU — 66.67%
これらの確率を掛け合わせると23.40%になります。4対1の配当を得ると、4 × 23.40% = 93.60%のリターンになります。つまり、ハウスエッジは6.40%です。ですから、この賭けはそのままにしておきます。
ディーラーが 22 でバストした場合に 11 対 1 で支払われる「プッシュ 22」ブラックジャックのバリエーションのサイド ベットを作成したいと考えています。オッズはどれくらいでしょうか?
ディーラーが 22 でバストした場合に勝つ「プッシュ 22」ブラックジャックのバリエーションにサイド ベットを作成しようと考えています。支払われるオッズはどのくらいで、ハウス エッジはいくらでしょうか?
ディーラーが常にハンドをドローアウトすると仮定すると (すべてのプレイヤーがすでにバストしている場合でも)、ディーラーがソフト 17 でスタンドする場合、22 でバストする確率は 7.88%、ソフト 17 をヒットする場合は 8.00% になります。
ディーラーがソフト17を出したと仮定すると、勝率が11対1の場合、ハウスエッジは4.04%になります。勝率が10対1の場合は、ハウスエッジは12.04%に跳ね上がります。
これはカウント可能だとプレイヤーに警告してアドバイスしておくべきでしょう (Wiz は黙れ!)。
エイミーとボブは、公平なコインを4回投げてどちらが先に勝つか競います。エイミーは、自分が勝つために8,000ドルを賭けたいと考えています。しかし、一度に賭けることができるのは1回だけです。すべての賭けの配当は均等です。エイミーが全勝すれば8,000ドルの利益を得て、ボブが全勝すれば8,000ドルの損失を被るように、エイミーはどのように賭け金を組めばよいでしょうか。
答えについては下のボタンをクリックしてください。
シリーズ中盤には16通りの状態が考えられます。以下の表は、この戦略に従ってエイミーが各状態において賭けるべき金額と、賭け前の残高を示しています。
答え
| エイミー | ボブ | バランス | ベット |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
解決策については下のボタンをクリックしてください。
させて:
- a = エイミーが勝つ
- b = ボブが勝つ
- w = エイミーのこれまでのシリーズ純勝利数
- f(a,b,w) = エイミーの次のゲームの賭け金
このようなパズルでは、最初から最後まで解き、最後から始めていくのが一般的に良い戦略です。とはいえ、次の点は容易に理解できます。
f(3,3,0) = 8,000
この状況では、7ゲーム目は「勝者総取り」となります。エイミーの勝ち金は0ドルで、最後のフリップに8,000ドルを賭けます。つまり、フリップに勝てば8,000ドルの勝ち、負ければ8,000ドルの負けとなります。
少し戻って、彼女が3勝、ボブが2勝していたらどうなるでしょうか。もし彼女が次のフリップで勝てば、ゲーム全体で彼女が勝ちます。もし彼女が負ければ、彼女のスコアは3-3になります。f(3,3,0)から、スコアが3,3なら彼女の手札は0になるはずです。つまり、彼女が次のフリップで勝てば8,000、そうでなければ0になるはずです。ここで得られるのは、4,000の中間の純利益と、同額のベットです。つまり、
f(3,2,4000)=4,000
もう一歩戻って、彼女が3勝、ボブが1勝だったとしましょう。もし彼女が次のフリップで勝てば、ゲーム全体の勝利となります。もし彼女が負ければ、彼女のスコアは3-2になります。f(3,2,4000)から、スコアが3.2なら彼女は4,000を獲得するはずです。つまり、彼女が次のフリップで勝てば8,000、そうでなければ4,000を獲得する必要があります。ここで得られるのは、中間の純利益[(4,000+8,000)/2=6,000]と、その2つのゴールの間の距離の半分[(8000-4000)/2=2000]の賭け金です。つまり、
f(3,1,6000) = 2,000
もう一歩戻って、彼女が3勝、ボブが0勝だったとしましょう。もし彼女が次のフリップで勝てば、ゲーム全体の勝利となります。もし彼女が負ければ、彼女のスコアは3-1になります。f(3,1,6000)から、スコアが3-1なら彼女は6,000を獲得するはずです。つまり、彼女が次のフリップで勝てば8,000、そうでなければ6,000を獲得する必要があります。ここで得られるのは、中間の純利益[(6,000+8,000)/2=7,000]と、その2つのゴールの間の距離の半分[(8000-4000)/2=2000]の賭け金です。つまり、
f(3,0,7000) = 1,000
スコアが同点になった場合、エイミーの純利益は0となるのは明らかでしょう。同点になった場合、彼女がシリーズ全体で勝利する確率は50%です。どちらの場合でも、勝敗は8,000ポイントずつというバランスの取れた目標値であるため、彼女は0ポイントで賭けなければ、どちらの最終目標も達成できない可能性があります。
次に、エイミーがシリーズで負けた場合、彼女の純利益は、同じスコアでリードしていた場合の純利益の-1倍になるはずです。例えば、エイミーのスコアが2 - ボブのスコアが3(または2-3)だとします。彼女が次のフリップで負ければ、ゲーム全体で負けとなります。彼女が勝てば、彼女のスコアは3-3になります。f(3,3,0)から、スコアが3,3の場合、彼女の純利益は0になるはずです。つまり、彼女が次のフリップで勝った場合は0、そうでない場合は-8000になる必要があります。ここで得られる純利益は、4,000の中間値と同額のベットです。つまり、次のようになります。
f(2,3,-4000)=4,000
同じ論理で言えば:
f(1,3,-6000) = 2,000
f(0,3,-7000) = 1,000
次に、スコアが2-2の場合、エイミーはいくら賭けるべきでしょうか?もし彼女がフリップに勝てば、スコアは3-2になります。上記の結果から、このスコアでは彼女は4,000の純利益を得る必要があることがわかります。また、もし彼女が2-3で負けているなら、彼女の純損失は4,000になるはずです。したがって、彼女は4,000を賭ける必要があります。
f(2,2,0) = 4,000
そこから一歩戻って、スコアが2-1の場合はどうなるでしょうか?次のフリップで勝った場合(スコア3-1)、ネット勝利額が6,000ドル必要で、負けた場合(スコア2-2)はネット勝利額が0ドル必要だと分かっています。ここで得られるのは、中間のネット勝利額[(6,000+0)/2=3,000]と、その2つのゴール間の距離の半分[(6,000-0)/2=3,000]です。つまり、
f(2,1,3000) = 3000
そこからさらに一歩戻って、彼女が2勝、ボブが0勝だったとしましょう。もし彼女が次のフリップで勝てば、スコアは3-0になります。彼女が負ければ、2-1になります。彼女は3-0で7000、2-1で3000の純利益を得るはずです。2-0のスコアから得られるのは、中間の純利益[(7,000+3,000)/2=5,000]と、その2つのゴールの間の半分の賭け金[(7000-3000)/2=2,000]です。つまり、
f(2,0,5000) = 2000
アリスが 2 回勝ち、ボブがそれより少ないスコアを反転すると、次のこともわかります。
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
前述の通り、シリーズが均衡している場合、エイミーの純利益は0になるはずです。つまり、1-1のスコアでは、彼女の純利益は0になるはずです。2-1のスコアでは2,000の利益が必要で、1-2のスコアでは2,000の損失が必要です。したがって、1-1の同点スコアでは、彼女は2,000を賭けるべきです。つまり、
f(1,1,0) = 2,000
エイミーが1-0でリードしていたらどうなりますか?2,0の時点で5,000ポイントリードしている必要があることは分かっています。1-1の時点では、エイミーは同点である必要があります。1-0のスコアから得られるのは、中間の純利益[(5,000+0)/2=2,500]と、その2つのゴール間の距離の半分[(5000-0)/2=2,500]の賭け金です。つまり、
f(1,0,2500) = 2,500
スコアを0-1にすると:
f(0,1,-2500) = 2,500
最終的に、0-0で最初のゲームに臨みます。エイミーが次のフリップで勝てば2,500ポイントの利益、負ければ2,500ポイントの損失が必要です。つまり、2,500ポイントを賭ければ、このゲームを達成できます。または、
f(0,0,0) = 2,500
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
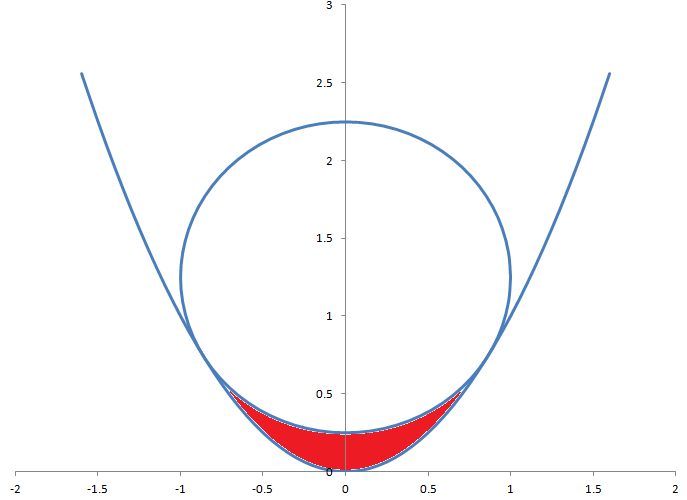
半径1の円は、方程式y=x 2の放物線に接しています。円と放物線の間の赤い領域の面積はいくらですか?
答えについては下のボタンをクリックしてください。
これが私の解決策です。(PDF)
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
この問題は、Mind Your Decisionsの Presh Talwalker さんから知りました。


