Wizardに尋ねる #326
クラップスにおけるアイアンクロス戦略とは何ですか?またそれについてどう思いますか?
アイアン クロスは、7 以外のサイコロの目が出ることを予想して、フィールド ベットとプレース ベットを賭ける方法です。フィールドには、2、3、4、9、10、11、12 がすでに含まれています。プレーヤーは、7 以外の残りの数字をカバーするために、5、6、8 のプレース ベットを追加します。次の表は、フィールド ベットに 5 ドル、5 のプレース ベットに 5 ドル、6 と 8 のプレース ベットに 6 ドルを賭けた場合の計算を示しています。
鉄十字
| サイコロの合計 | 勝つ | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| 2 | 10 | 1 | 0.027778 | 0.277778 |
| 3 | 5 | 2 | 0.055556 | 0.277778 |
| 4 | 5 | 3 | 0.083333 | 0.416667 |
| 5 | 2 | 4 | 0.111111 | 0.222222 |
| 6 | 2 | 5 | 0.138889 | 0.277778 |
| 7 | -22 | 6 | 0.166667 | -3.666667 |
| 8 | 2 | 5 | 0.138889 | 0.277778 |
| 9 | 5 | 4 | 0.111111 | 0.555556 |
| 10 | 5 | 3 | 0.083333 | 0.416667 |
| 11 | 5 | 2 | 0.055556 | 0.277778 |
| 12 | 15 | 1 | 0.027778 | 0.416667 |
| 36 | 1.000000 | -0.250000 |
表の右下のセルには、予想損失額が$0.25と表示されています。賭け金の合計は$22です。したがって、ハウスエッジは$0.25/$22 = 1/88 = 1.14%となります。
この時点で、このハウスエッジが個々のベットのハウスエッジよりも低いのはなぜかと疑問に思うかもしれません。答えは、6と8に賭けた場合のハウスエッジが1.52%、5に賭けた場合のハウスエッジが4.00%であり、これはベットの成立回数に基づいているためです。プレースベットのハウスエッジをロールごとに定義すると、6または8に賭けた場合のハウスエッジは0.46%、5に賭けた場合のハウスエッジは1.11%となります。
以下のように、すべての賭けの加重平均を取ると、1.14% のハウス エッジが得られます。
($5*2.78% + $5*1.11% + $12*0.46%)/22 = $0.25/$22 = 1.14%。
フィールドベットで12倍の配当しか支払わないカジノには注意しましょう。3倍の配当を主張しましょう。ショートペイは、そのベットのハウスエッジを2.78%から5.56%へと倍増させます。
私の意見としては、ほとんどのゲームと比較すると、1.14%はかなり良い賭け方だと思います。しかし、クラップスではもっと良い賭け方があります。例えば、オッズが3倍、4倍、5倍で、パスとカムにフルオッズで賭けると、ハウスエッジは0.37%まで下がります。逆に、ドントパスとドントカムに賭け、さらにフルオッズで賭けると、ハウスエッジは0.27%になります。公平なサイコロを振った場合、すべての面を少なくとも 2 回振る期待回数は何回ですか。
これは長くて面倒なマルコフ連鎖で解くこともできますが、私は積分解法を好みます。この手法の使い方については、ファイアベットとボーナスクラップスのページで説明しています。
重要な出来事がサイコロの目によって一つずつ決まるのではなく、一つの瞬間として捉えると想像してみてください。出来事間の時間は記憶を持たない性質を持ち、出来事間の平均時間は1単位時間であると仮定します。言い換えれば、出来事間の時間は平均1の指数分布に従います。賭けの判定においては、これは問題になりません。なぜなら、出来事は依然として一つずつ起こるからです。
ポアソン分布によれば、サイコロの任意の面がx単位時間内に0回振られる確率はexp(-x/6)*(x/6) 0 /0! = exp(-x/6) です。ポアソン分布によれば、任意の面がちょうど1回振られる確率はexp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6) です。したがって、任意の面がx単位時間内に2回以上振られる確率は1 - exp(-x/6)*(1 + (x/6))) 6です。少なくとも1つの面が2回以上振られていない確率は次の式で表されます。
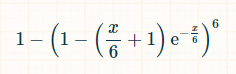
望ましい目標が達成されないまま平均してどのくらいの時間が経過するかを調べるには、これを全時間にわたって積分する必要があります。
幸いなことに、この時点で積分計算機を使うことができます。リンク先の計算機では、「積分を計算」の後のテキストボックスに 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 と入力し、カスタムで積分範囲を0から∞に設定します。
答えは390968681 / 16200000 = 約24.13386919753086です。
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
質問は2つあります。
パート 1 の場合:- x + y + z = 1
- x^2 + y^2 + z^2 = 4
- x^3 + y^3 + z^3 = 9
x^4 + y^4 + z^4 とは何ですか?
2 番目の部分では、次のような一般的なケースの答えは何ですか。
- x + y + z = a
- x^2 + y^2 + z^2 = b
- x^3 + y^3 + z^3 = c
問1: 97/6 = 約16.166666
問2: a 4 /6 + (4/3)ac - a 2 b + b 2 /2
私の解決策(PDF)をご覧ください
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
まず、公平な6面サイコロを6回振り、それぞれの出目を記録します。次に、これらの数字を、ラベルのない別の公平なサイコロの6面に書き込みます。例えば、6回振った結果が3、5、3、6、1、2だった場合、2回目のサイコロには4ではなく、3が2つ出ます。
次に、この2つ目のサイコロを6回振ります。その6つの数字を、さらに別の公平なサイコロの面に書き込み、前のサイコロから新しいサイコロを生成するというプロセスを続けます。
最終的に、6面全てに同じ目が出るサイコロになります。この状態に至るまでの、サイコロの出目遷移の平均回数(または合計出目を6で割った回数)はいくつですか?
混乱を避けるため、最初のサイコロには数字ではなく文字でラベルを付けましょう。それぞれのサイコロの状態にも文字を付けましょう。例えば、AAABBCは、ある文字が3つ、別の文字が2つ、そして別の文字が1つ出ていることを意味します。最初の状態は明らかにABCDEFです。
E(ABCDEF) を状態 ABCDEF からの期待ロール数とします。
E(ABCDEF) = 1 + [180 × E(AAAAB) + 450 × E(AAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656ある状態から別の状態へ遷移する組み合わせの数に基づいて、以下の遷移行列は、各初期状態(左の列)から各新しい状態へ遷移する方法が何通りあるかを示しています。ちなみに、これを正しく構築するには数時間かかりました。
遷移行列A
| 州 前に | ああああ | ああああ | ああああ | AAABBB | AAAABC | AAABBC | AABBCC | AAAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ああああ | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| ああああ | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| AAABBC | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| AABBCC | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| AAAABCD | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| AABBCD | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| AABCDE | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
行列代数についての長い講義はしませんが、行列 B は次のようになると仮定します。
マトリックスB
| 州 前に | ああああ | ああああ | AAABBB | AAAABC | AAABBC | AABBCC | AAAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| ああああ | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| ああああ | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| AABBCC | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| AABBCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| AABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
答えは行列 B と行列 A の行列式です。
決定(A) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000
決定(B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = 約9.65599148388557


