Wizardに尋ねる #335
Wizard of Vegasの記事で、リバーシブルロイヤルのリターンが105.22%だと読みました。このリターンは、カードの順番を含めた最適な戦略を前提としています。平均的なロイヤル勝利を前提とした場合のリターンはどれくらいでしょうか?また、基本ペイテーブルである通常の6-5ボーナスポーカー戦略を使った場合はどうでしょうか?
戦略の逸脱がないと仮定すると、60回中1回は連続ロイヤルとなります。リバーシブルロイヤルジャックポットは1回につき161,556の配当となります。その他のロイヤルは1回につき800の配当となります。したがって、ロイヤルの平均配当は(1/60)*161,556 + (59/60)*800 + 1回につき17,396となります。
すべてのロイヤルが 17,396 を支払うと仮定し、そのロイヤルの勝利に基づいて最適な戦略を実行すると、リターンは 103.56% に低下します。
基本ペイテーブルである標準的な 6-5 ボーナス ポーカー戦略をプレイすると、リターンはさらに 101.97% に低下します。
座標が(0,0)、(1,0)、(1,1)、(0,1)の単位正方形を考えます。直線Aは(0,0)から(1,1)まで伸びています。直線Bは(1,0)から(0.5,1)まで伸びています。直線A、直線B、そして円の底辺に接する円の半径はいくらでしょうか?
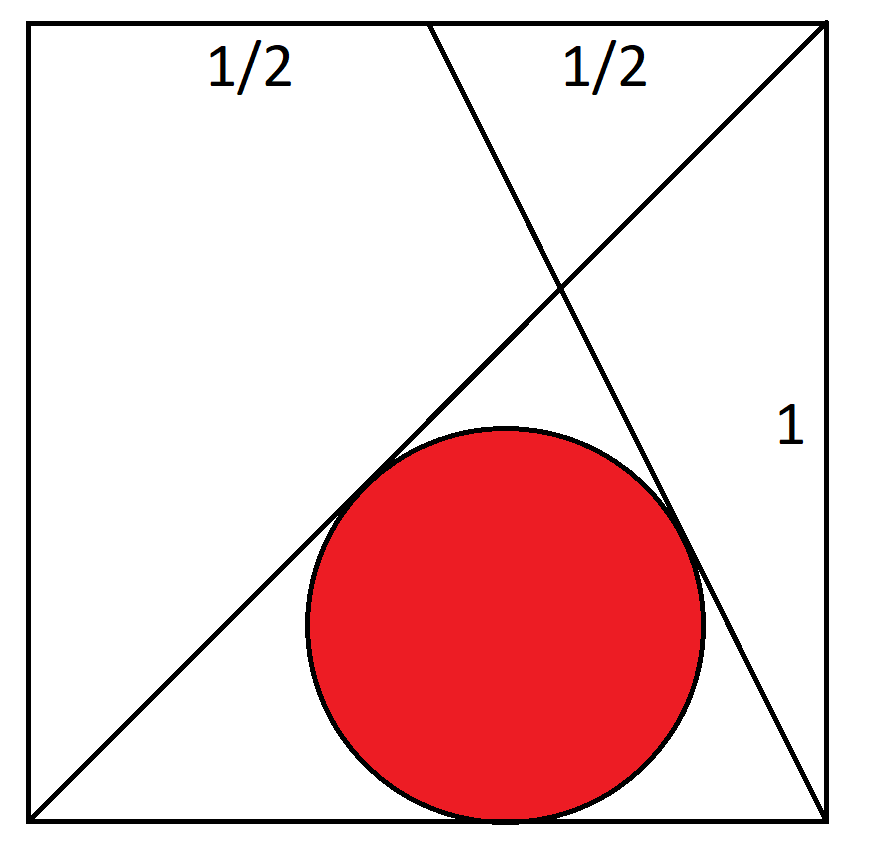
このパズルはMensa Bulletinの2020年10月号に掲載されました。
[ネタバレ=ヒント]tan(2x)=2tan(x)/(1-tan 2 (x))[/spoiler]
これが私の解決策です(PDF)。
この問題は、 Wizard of Vegasの私のフォーラムで質問され、議論されています。
それがカードに残っている唯一のカテゴリーである場合、Yahtzee を取得する確率はどれくらいですか?
Yahtzeeをご存知ない読者のために説明すると、これは5個のサイコロを3回振ったときに、5の目が同じ目になる確率を問うものです。サイコロを振るたびに、どのサイコロを保管し、どのサイコロを振り直すかを選択する必要があります。
以下は、最初のロール、またはプレイヤーが 4 個または 5 個のサイコロを振った後の可能な結果です。
- 5枚揃い = 6*(1/6)^5 = 0.000772
- フォー・オブ・ア・カインド = (1/6)^3*(5/6)*4 = 0.015432
- スリー・オブ・ア・カインド = (1/6)^2*(5/6)^2*COMBIN(4,2) = 0.115741
- 2枚揃い = 4*(1/6)*(5/6)^3 = 0.385802
- 唯一無二 = 6*5!/6^5 = 0.092593
ペアを保持した後の確率は次のとおりです。
- 5枚揃い =(1/6)^3 = 0.004630
- フォー・オブ・ア・カインド = 3*(1/6)^2*(5/6) = 0.069444
- スリーオブアカインド = 3*(1/6)*(5/6)^2+5*(1/6)^3 = 0.370370
- 2枚揃う = (5/6)^3-5*(1/6)^3 = 0.555555
スリーオブカインドを保持した後の確率は次のとおりです。
- 5枚揃い =(1/6)^3 = 0.002778
- フォー・オブ・ア・カインド = 2*(1/6)*(5/6) = 0.27778
- スリーオブアカインド = (5/6)^2 = 0.694444
フォー・オブ・ア・カインドを保持した後の確率は次のとおりです。
- 5枚の同じカード = 1/6 = 0.166667
- フォー・オブ・ア・カインド = 5/6 = 0.83333
これらの進出確率を踏まえ、2 回目のロール後の各州の進出確率は次のとおりです。
- 5枚の同じカード = 0.000772 + 0.015432*0.166667 + 0.115741*0.002778 + 0.385802*0.004630 + 0.092593* 0.000772 = 0.012631
- フォー・オブ・ア・カインド = 0.015432*0.166667 + 0.115741*0.27778 + 0.115741*0.27778 = 0.116970
- スリー・オブ・ア・カインド = 0.115741*0.694444 + 0.385802*0.370370 + 0.092593*0.115741 = 0.409022
- 2枚揃い = 0.385802*0.555555 + 0.092593*0.385802 = 0.450103
- 唯一無二 = 0.092593 * 0.092593 = 0.008573
同じ前進の確率を使用して、3 回目のロール後に Yahtzee が出る確率は次のとおりです。
5枚の同じカード = 0.012631 + 0.116970*(1/6) + 0.409022*(1/6)^2 + 0.450103*(1/6)^3 + 0.008573*(1/6)^4 = 0.046029。
行列代数を好む人のために、遷移行列があります。
| 0.092593 | 0.694444 | 0.192901 | 0.019290 | 0.000772 |
| 0.000000 | 0.555556 | 0.370370 | 0.069444 | 0.004630 |
| 0.000000 | 0.000000 | 0.694444 | 0.277778 | 0.027778 |
| 0.000000 | 0.000000 | 0.000000 | 0.833333 | 0.166667 |
| 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
上記の行列を M とすると、 3 回のロール後の状態は次のように M 3になります。
| 0.000794 | 0.256011 | 0.452402 | 0.244765 | 0.046029 |
| 0.000000 | 0.171468 | 0.435814 | 0.316144 | 0.076575 |
| 0.000000 | 0.000000 | 0.334898 | 0.487611 | 0.177491 |
| 0.000000 | 0.000000 | 0.000000 | 0.578704 | 0.421296 |
| 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
3 回のロール後に Yahtzee が出る確率は、右上隅のセルに表示されます。
クイーンズ・ギャンビットを最後まで観て、番組で流れていたゲームがどれも引き分けで終わっていないことに気づきました。チェスではハイレベルな試合は引き分けが多いと思っていたのですが、グランドマスターレベルのチェスでは、引き分けで終わる割合はどれくらいですか?
ChessBase.com の記事「チェスの引き分けの数は増加したか?」によると、著者の Qiyu Zhou 氏は、レート 2600 以上 (グランドマスターになるには 2500 が必要) のプレイヤー間の 78,468 回のレート付きゲームで、次のような結果になったと述べています。
- 黒の勝ち: 18.0%
- 白の勝ち: 28.9%
- 引き分け: 53.1%


