Wizardに尋ねる #338
2 個のサイコロを振って 2 から 12 までの合計を出すのに必要な平均回数はいくつですか。
正方形の真ん中にアリがいます。アリは左上隅から17インチ、右上隅から20インチ、右下隅から13インチのところにいます。
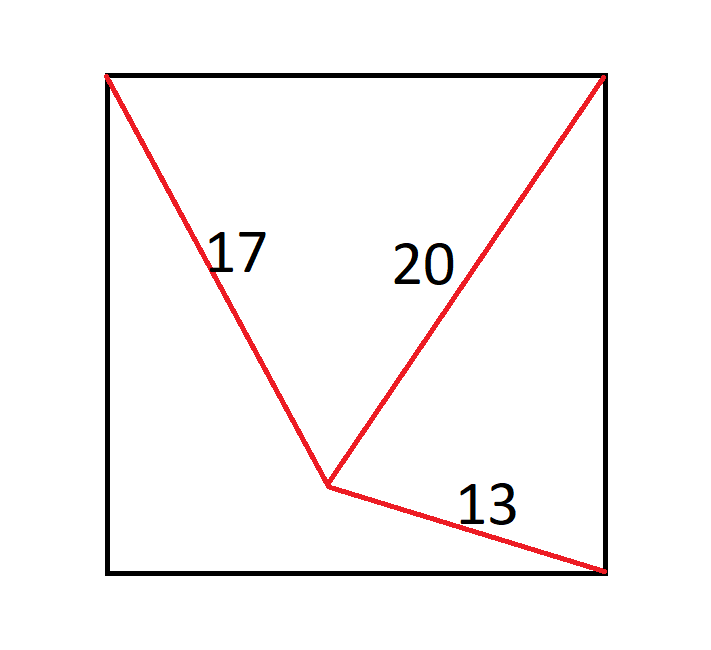
広場の大きさはどれくらいですか?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
まず、三角形 ABE を 90 度回転して、新しい三角形 BDF を形成します。
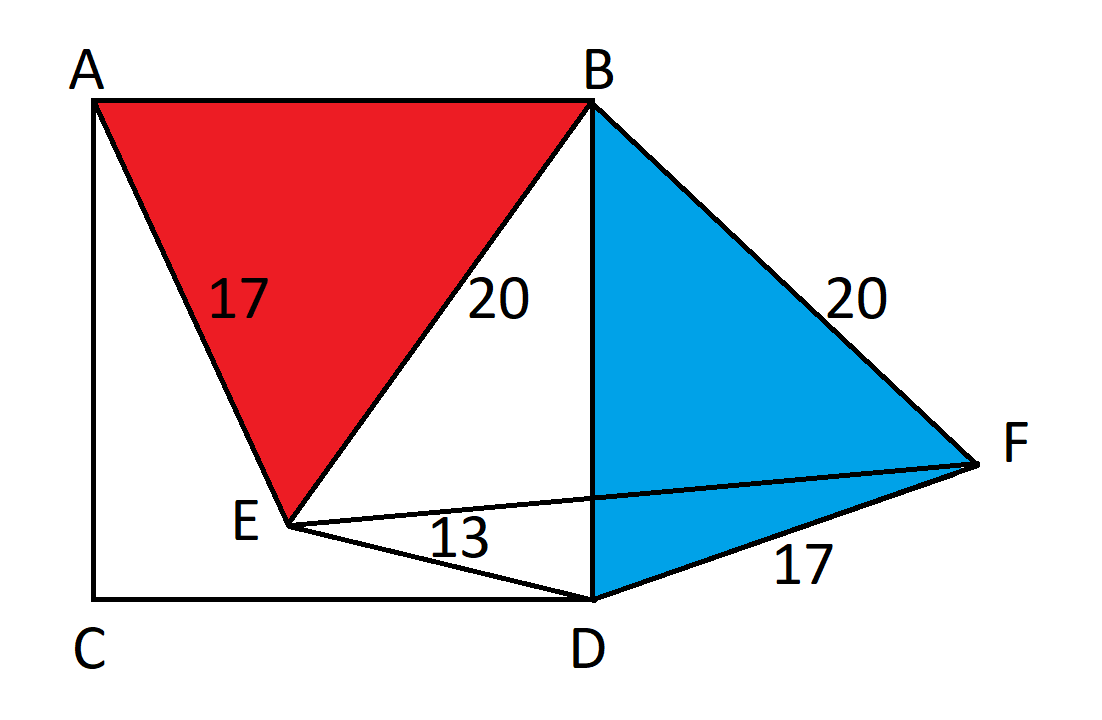
三角形は90度回転しているので、定義により、角EBF=90となります。ピタゴラスの定理によれば、EF = 20*sqrt(2)となります。
余弦定理によれば、17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF)となります。
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680。
cos(DEF) = 17*sqrt(2)/26。
sin^2(x) + cos^2(x) = 1 を思い出してください。これを使って sin(DEF) を解きましょう。
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
次に、角度 BED について考えます。
角度 BED = 角度 BEF + 角度 FED。
EBFは90度で二等辺三角形であることが分かっています。つまり、BEFの角度は45度になります。
つまり、角度 BED = 45 度 + 角度 FED となります。
思い出してください、cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)。
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
今度は三角形 BED に余弦定理をもう一度適用してみましょう。
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD は問題の正方形の辺なので、BD^2 はその正方形の面積であり、369 であることが示されています。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
ドロップデッドは、5つの標準的なサイコロを使ってプレイするゲームです。プレイヤーは5つのサイコロを全て振ることから自分のターンを開始します。2と5が出なかった場合、サイコロの出目を合計し、その合計を自分のポイントスコアに加えて、もう一度サイコロを振ります。2または5が出た場合、そのロールのスコアは0になります。2または5が出たサイコロはすべてデッド(死)と宣言され、脇に置きます。残りのサイコロでもう一度サイコロを振ります。ゲームは、ポイントを獲得するか、サイコロを取り除いて続行されます。すべてのサイコロが除去された時点でターンは終了し、ドロップデッド(死んだ)とみなされます。すべてのロールのスコアが合計され、最終スコアが算出されます。高スコアのプレイヤーが勝ちます。
このゲームの予想スコアはいくらですか?
サイコロが 1 個残っているシナリオから始めて、後方へ進んでみましょう。
変数 a を、サイコロが 1 個残った場合に期待される追加ポイントとします。
2 または 5 以外の目が出る場合の平均は (1+3+4+6)/4 = 7/2 です。
a = (2/3)×(a + 7/2)。
a/3 = 7/3 です。
a = 7 です。
次に、サイコロが 2 個残ったときの期待値である b を計算します。
b = (2/3) 2 × (b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.
b = 11.2です。
次に、サイコロが 3 個残ったときの期待値 c を計算します。
c = (2/3) 3 × (c + 3× (7/2)) + 3×(2/3) 2 × (1/3)×b + 3×(2/3)×(1/3) 2 ×b。
c = 1302/95 = 13.705263 です。
次に、サイコロが 4 個残ったときの期待値 d を計算してみましょう。
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a。
d = 3752/247 = 15.190283.
最後に、残り 5 個のサイコロで予想されるポイント e を計算しましょう。
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a。
e = 16.064662 です。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
スリーカードポーカーのペアプラスベットを考えてみましょう。これは1-4-6-30-40の配当表に従います。ただし、スペードのミニロイヤルでジャックポットが支払われ、他の3つのスーツのミニロイヤルではそのジャックポットの25%が支払われます。このベットが公平であるためには、メーターはどれくらい高くなければなりませんか?


