WOO logo

Wizard のオススメ

Wizardに尋ねる #340

カジノがタイベットの勝ちを通常の8対1よりも9対1に増やした場合、同じ予想勝ちを得るにはタイにいくら分の追加ベットが必要になりますか？

dandolos2000

バカラで同点になる確率は0.095155968です。The probability of a tie in baccarat is 0.095155968.

通常の8対1の勝利では、プレイヤーへの期待収益は0.095156 × (8+1) - 1 = -0.143596です。

9対1の勝利で、プレイヤーへの期待収益は0.095156 × (9+1) - 1 = --0.048440です。

予想されるプレイヤーの損失は、8対1の勝利で0.143596 / 0.048440 = 2.9643960倍ほど高くなります。したがって予想されるカジノの勝利を9対1に増やした場合、カジノは同じ引き分けになるためには2.9643960倍のアクションを必要とします。

この質問は、私のコンパニオンサイトである Wizard of Vegas のフォーラムにて提起および議論されました。

1から100までの番号が付けられたボールが100個入った箱があるとします。10個のボールが無作為に、非置換で抽出されます。抽出されたボールの中で最も低い番号のボールの平均はいくつですか？

ThatDonGuy

以下の表は、組み合わせの数、確率、そして最低のボールへの寄与度（ボールと確率の積）を示しています。右下のセルは、期待される最低のボールが9.1818182であることを示しています。

最低ボール

最低
ボール		組み合わせ確率期待される
ローボール
1 1,731,030,945,644 0.100000 0.100000
2 1,573,664,496,040 0.090909 0.181818
3 1,429,144,287,220 0.082560 0.247681
4 1,296,543,270,880 0.074900 0.299600
5 1,174,992,339,235 0.067878 0.339391
6 1,063,677,275,518 0.061448 0.368686
7 961,835,834,245 0.055564 0.388950
8 868,754,947,060 0.050187 0.401497
9 783,768,050,065 0.045278 0.407498
10 706,252,528,630 0.040800 0.407995
11 635,627,275,767 0.036720 0.403915
12 571,350,360,240 0.033006 0.396076
13 512,916,800,670 0.029631 0.385199
14 459,856,441,980 0.026565 0.371917
15 411,731,930,610 0.023785 0.356780
16 368,136,785,016 0.021267 0.340271
17 328,693,558,050 0.018988 0.322801
18 293,052,087,900 0.016929 0.304728
19 260,887,834,350 0.015071 0.286354
20 231,900,297,200 0.013397 0.267933
21 205,811,513,765 0.011890 0.249680
22 182,364,632,450 0.010535 0.231771
23 161,322,559,475 0.009319 0.214347
24 142,466,675,900 0.008230 0.197524
25 125,595,622,175 0.007256 0.181388
26 110,524,147,514 0.006385 0.166007
27 97,082,021,465 0.005608 0.151425
28 85,113,005,120 0.004917 0.137673
29 74,473,879,480 0.004302 0.124766
30 65,033,528,560 0.003757 0.112708
31 56,672,074,888 0.003274 0.101491
32 49,280,065,120 0.002847 0.091100
33 42,757,703,560 0.002470 0.081512
34 37,014,131,440 0.002138 0.072701
35 31,966,749,880 0.001847 0.064634
36 27,540,584,512 0.001591 0.057276
37 23,667,689,815 0.001367 0.050589
38 20,286,591,270 0.001172 0.044534
39 17,341,763,505 0.001002 0.039071
40 14,783,142,660 0.000854 0.034160
41 12,565,671,261 0.000726 0.029762
42 10,648,873,950 0.000615 0.025837
43 8,996,462,475 0.000520 0.022348
44 7,575,968,400 0.000438 0.019257
45 6,358,402,050 0.000367 0.016529
46 5,317,936,260 0.000307 0.014132
47 4,431,613,550 0.000256 0。012032
48 3,679,075,400 0.000213 0.010202
49 3,042,312,350 0.000176 0.008612
50 2,505,433,700 0.000145 0.007237
51 2,054,455,634 0.000119 0.006053
52 1,677,106,640 0.000097 0.005038
53 1,362,649,145 0.000079 0.004172
54 1,101,716,330 0.000064 0.003437
55 8億8,616万3,135 0.000051 0.002816
56 708,930,508 0.000041 0.002293
57 5億6392万1995 0.000033 0.001857
58 4億4589万1810円0.000026 0.001494
59 3億5034万3565 0.000020 0.001194
60 2億7343万8880円0.000016 0.000948
61 2億1191万5132 0.000012 0.000747
62 1億6301万1640 0.000009 0.000584
63 1億2440万3620 0.000007 0.000453
64 94,143,280 0.000005 0.000348
65 70,607,460 0.000004 0.000265
66 52,451,256 0.000003 0.000200
67 38,567,100 0.000002 0.000149
68 28,048,800 0.000002 0.000110
69 20,160,075 0.000001 0.000080
70 14,307,150 0.000001 0.000058
71 10,015,005 0.000001 0.000041
72 6,906,900 0.000000 0.000029
73 4,686,825 0.000000 0.000020
74 3,124,550 0.000000 0.000013
75 2,042,975 0.000000 0.000009
76 1,307,504 0.000000 0.000006
77 817,190 0.000000 0.000004
78 497,420 0.000000 0.000002
79 293,930 0.000000 0.000001
80 167,960 0.000000 0.000001
81 92,378 0.000000 0.000000
82 48,620 0.000000 0.000000
83 24,310 0.000000 0.000000
84 11,440 0.000000 0.000000
85 5,005 0.000000 0.000000
86 2,002 0.000000 0.000000
87 715 0.000000 0.000000
88 220 0.000000 0.000000
89 55 0.000000 0.000000
90 10 0.000000 0.000000
91 1 0.000000 0.000000
合計17,310,309,456,440 1.000000 9.181818

このような、最も低いボールが1である問題を解くには、もっと簡単な方法があります。最も低いボールの公式は(m+1)/(b+1)です。ここで、mはボールの最大値、bはボールの数です。この場合、m=100、n=10なので、最も低いボールは101/11 = 9.181818となります。

この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

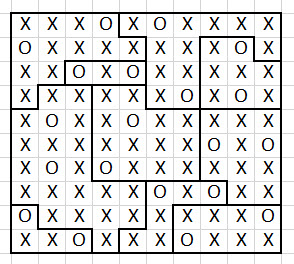
次のパズルは、2021 年 3 月 6 日のニューヨーク タイムズに掲載されました。

ルールは非常に簡単です:

  1. 各行、列、領域には、必ず 2 つの星が必要です。
  2. 2 つの星は、たとえ斜めであっても接触してはいけません。

解決策を教えていただけますか?

匿名

これは「ツー・ノット・タッチ」パズルと呼ばれています。下のボタンをクリックすると、私の答えと解答が表示されます。

2つは触れずに解決

これが私の解決策です（PDF）。

公平な 6 面サイコロを振った場合、どの面も 6 回振られると予想される回数はいくつですか。

Ace2

私の回答については下のボタンをクリックしてください。

答えは 2597868106693535971 / 131621703842267136 = 近似値: 19.73738396371749

これが私の解決策です（PDF）。