Wizardに尋ねる #341
2つのサイコロを振って、2から12までの合計が出るまでの予想回数はいくつですか? 微積分を使って答えてください。
合計が2になる確率は1/36であることを思い出してください。t回振った場合、合計が2になる期待値はt/36です。振る間隔は平均t/36の指数分布に従うと仮定します。ポアソン分布によれば、合計が2になる0回の確率はexp(-t/36)です。
合計が3になる確率は2/36 = 1/18であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が3でサイコロが0回出る確率はexp(-t/18)となります。
合計が4になる確率は3/36 = 1/12であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が4でサイコロが0回出る確率はexp(-t/12)となります。
合計が5になる確率は4/36 = 1/9であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が5でサイコロが0回出る確率はexp(-t/9)となります。
合計が6になる確率は5/36であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が6でサイコロが0回出る確率はexp(-5t/36)となります。
合計が7になる確率は6/36 = 1/6であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が7でサイコロが0回出る確率はexp(-t/6)となります。
8 から 12 までの確率は 2 から 6 までの確率と同じです。
したがって、t 単位のあらゆる合計が少なくとも 1 回ロールされる確率は次のとおりです。
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
t単位の時間内に少なくとも合計が出ていない確率は、1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))です。
少なくとも 1 つの合計なしで予想時間を取得するには、上記の関数を 0 から無限大まで積分します。
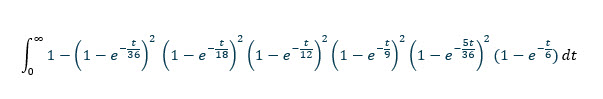
積分計算機 (これをお勧めします) を使用すると、769767316159/12574325400 = 約 61.2173847639572 ロールとして簡単に解くことができます。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
赤いサイコロと青いサイコロを2つ繰り返し振ります。それぞれのサイコロの出目の合計を記録します。2つのサイコロの合計が等しくなるまで、何個のサイコロを振ると予想されますか?
なぜ答えが無限大なのかを説明するのは難しい。さらに混乱を招き、逆説的なのは、合計が等しくなる確率が1であることだ。
次の表は、1 回目から 16 回目のロール後に初めて合計が同じになる確率を示しています。
確率合計が初めて等しくなる
| ロール | 確率 |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 13 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
Excel では、この曲線に非常に近い値は y = 0.1784*x-1.011 であると示されています。ここで、x = ロール回数、y = 確率です。
この無限級数の合計は無限大です。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
ペンシルバニア・キャッシュ5ゲームの損益分岐点ジャックポットはいくらですか?税金とジャックポットの分配は無視できます。
まず、ルールを確認しましょう。賭け金は2ドルです。このゲームは43個のボールの中から5個を引くことで成立します。配当表はこちらです。
- 5つマッチ = ジャックポット
- 数学4 = 200ドル
- マッチ3 = $10
- マッチ2 = $2
さらに、プレイヤーはスクラッチカードのようなものを受け取ります。これは6ドルが当たる確率が1/80、2ドルが当たる確率が1/5です。
以下の表は、ベースゲームの分析結果です。2~4個の数字を当てた場合の価値は0.287784ドルです。
キャッシュ5リターンテーブル
| キャッチ | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| 5 | ジャックポット | 1 | 0.000001 | ? |
| 4 | 200 | 190 | 0.000197 | 0.039477 |
| 3 | 10 | 7030 | 0.007303 | 0.073032 |
| 2 | 2 | 84360 | 0.087638 | 0.175276 |
| 1 | 0 | 369075 | 0.383416 | 0.000000 |
| 0 | 0 | 501942 | 0.521445 | 0.000000 |
| 合計 | 0 | 962598 | 1.000000 | 0.287784 |
以下の表は、クイックキャッシュのインスタントウィン機能に関する私の分析を示しています。右下のセルには0.475ドルの値が表示されています。
即時現金還元表
| キャッチ | 支払う | 確率 | 戻る |
|---|---|---|---|
| 6 | 1 | 0.012500 | 0.075000 |
| 2 | 16 | 0.200000 | 0.400000 |
| 0 | 63 | 0.787500 | 0.000000 |
| 合計 | 80 | 1.000000 | 0.475000 |
したがって、非プログレッシブ賞金の価値は、$0.287784 + $0.475000 = $0.762784 となります。
jを損益分岐点のジャックポットの価値と等しくすると、次のようになります。
2 = 0.762784 + j × (1/962598)
1.237216 = j × (1/962598)
j = 1.237216 × 962598
j = 1,190,941.95ドル。
全体的な収益率は、ジャックポットの 100,000 ドルごとに 0.381392 に 0.051943 を加算した値になります。
質問に述べられているように、これらすべては税金とジャックポットの分配を無視しています。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。


