Wizardに尋ねる #349
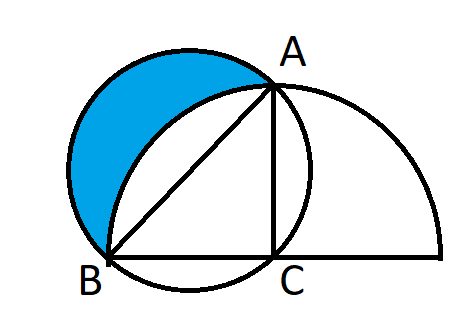
次の図で、青い領域の面積はどれくらいでしょうか?
ビデオポーカーでドロー後に保持されるカードの平均枚数はどれくらいですか?
以下の表は、10種類のゲームとペイテーブルにおける平均カード枚数を示しています。リストされているゲームの平均は2.05枚です。
ビデオポーカーで保持される平均カード
| ゲーム | ペイテーブル | 戻る | 平均カード保有数 |
|---|---|---|---|
| ボーナスデュース | 10-4-3-3 | 97.36% | 1.845550 |
| デュースワイルド | 25-15-9-5-3 | 100.76% | 1.926010 |
| ホワイトホットエース | 9-5 | 99.57% | 2.055630 |
| スーパーダブルダブルボーナス | 7-5 | 99.17% | 2.057280 |
| ダブルダブルボーナス | 9-5 | 97.87% | 2.058390 |
| トリプルダブルボーナス | 8-5 | 95.97% | 2.072620 |
| ボーナスポーカー | 8-5 | 99.17% | 2.080610 |
| ジャックス・オア・ベター | 9-5 | 98.45% | 2.081030 |
| ボーナスポーカーデラックス | 8-5 | 97.40% | 2.150470 |
| ダブルボーナス | 9-6-5 | 97.81% | 2.173550 |
チェスのトーナメントでは、各出場者は他の出場者全員と対戦します。各出場者は、勝った試合ごとに1ポイント、引き分けの試合ごとに0.5ポイント、負けた試合ごとに0ポイントを獲得します。
トーナメントの終了時には、すべての競技者がそれぞれ異なるポイント数を獲得し、スコアランキングの最下位の競技者が上位 3 名の競技者をそれぞれ破ったことがわかります。
したがって、トーナメントに参加する競技者の最小人数は何人ですか?
プレイヤーの数をnとしましょう。
最下位のプレイヤーは、上位3人のプレイヤーに対して3勝しか挙げられず、それ以外の試合はすべて負けていると考えられます。つまり、3ポイント獲得です。
次に、ポイント順で後続のプレイヤーを、前のプレイヤーより0.5ポイント多く獲得する(順位付け)。つまり、最高位のプレイヤーのポイントは3+(n-1)/2となる。
3 と 3+(n-1)/2 を 1 ステップあたり 1/2 ポイントずつ加算すると、(((n+5)*(n+6)/2)-15)/2 になります。
n人のプレイヤーがプレイするゲームの総数はn*(n-1)/2で、全員が他のプレイヤーと1回ずつ対戦します。各ゲームで合計1ポイントが加算され、これは全プレイヤーの獲得ポイントの合計でもあります。
次にnについて解きます。
(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n^2 + 11n = 2n^2 - 2n
n + 11 = 2n-2
n=13
以下の表は、これがどのように起こるかを示しています。表の本体には、78試合すべての勝者が示されています。
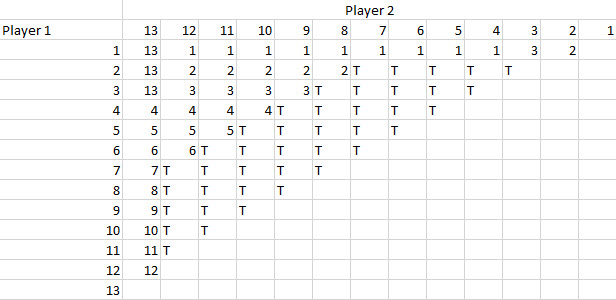
以下の表は各プレイヤーのポイント数を示しています。
プレイヤー別合計ポイント
| プレーヤー | ポイント |
|---|---|
| 13 | 3 |
| 12 | 3.5 |
| 11 | 4 |
| 10 | 4.5 |
| 9 | 5 |
| 8 | 5.5 |
| 7 | 6 |
| 6 | 6.5 |
| 5 | 7 |
| 4 | 7.5 |
| 3 | 8 |
| 2 | 8.5 |
| 1 | 9 |
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。


