Wizardに尋ねる #352
ミシシッピ スタッドでは、最大支払額によってハウス エッジがどの程度増加しますか?
いい質問ですね。ミシシッピ・スタッドのプレイヤーは、最大配当によってロイヤルフラッシュの勝ち額が減る可能性があり、それがハウスエッジの増加につながることを必ず認識しておくべきです。
ミシシッピスタッドの最高配当はロイヤルフラッシュで500倍で、すべてのベットに適用されます。プレイヤーはアンティの3倍までレイズできるチャンスが2回あるため、最終的なベットはアンティの7倍までとなります。ロイヤルフラッシュを期待するプレイヤーは、最大限にレイズするべきです。
ミシシッピスタッドでは、ペイアウトキャップの影響を受けずにアンティに賭けるべき最高額は、最大ペイアウト額÷3500です。例えば、最大ペイアウト額が80,000ドルの場合、アンティに賭けるべき最高額は22.86ドルです。私はこれを20ドルに切り捨てます。
以下の表は、様々なベット額におけるハウスエッジと一般的な最大勝利金を示しています。この表は、勝利金に上限を設けず、プレイヤーが最適な戦略でプレイすることを前提としています。ベット額が増加し、勝利金の上限が下がるにつれて、ハウスエッジが増加する点にご注目ください。
ペイアウトキャップ付きハウスエッジ
| ベット | 5万ドルの上限 | 8万ドルの上限 | 10万ドルの上限 |
|---|---|---|---|
| 15ドル | 5.02% | 4.91% | 4.91% |
| 20ドル | 5.15% | 4.91% | 4.91% |
| 25ドル | 5.22% | 5.04% | 4.91% |
| 50ドル | 5.38% | 5.28% | 5.22% |
| 75ドル | 5.49% | 5.37% | 5.33% |
| 100ドル | 5.64% | 5.41% | 5.38% |
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
Vital Vegasは、110万ドルのジャックポットに対し、わずか200ドルのチップしか渡さなかったプレイヤーを厳しく罰しました。このような状況でのチップの適切なエチケットは何でしょうか?
はい、彼らはチップの少額についてプレイヤーを叱責しながらも、適切なチップ額はいくらであるべきかという質問を都合よく避けています。
高額ジャックポットだけでなく、少額ジャックポットでもチップのマナーは明確に定義されていません。意見は様々で、その多くはジャックポットを当てたことのない人たちによるものです。
まず、チップは必須であることを強調しておきます。カジノでは、獲得した金額とサービスのレベルに応じて、受けたサービスに対してチップを払うことが求められています。ここまで来ると、ミスター・ピンクになって、なぜチップを払うべきではないのかと正当化するのは簡単です。チップ制度は確かに欠陥のあるシステムですが、それが私たちのシステムなのです。もしあなたが同意せず、チップを拒否するのであれば、チップが必要なサービスを頼まないでください。
次に、ジャックポットが成立したら、プレイヤーはチップをいくら支払うべきでしょうか?ここでは、プレイヤーが1つのジャックポットしか獲得できなかった場合を想定して議論します。高額ベットの場合、プレイヤーが複数のジャックポットを獲得するのはよくあることですが、その場合はルールが異なります。ジャックポットの申請手続きに関するルールは以下のとおりです。
- 「スロット」で1,200ドル以上を獲得。
- キノで1,500ドル以上を獲得。
- ポーカートーナメントで 5,000 ドル以上を獲得する。
- テーブル ゲームで 600 ドル以上、かつ賭け金の 300 倍以上の賞金を獲得。
チップの推奨額はいくらでしょうか?以前、ジャックポットの0.5%から2%とお伝えしましたが、ジャックポットが大きければ大きいほど、チップの割合は低くなります。しかし、当時はこれほど大きなジャックポットのことなど考えていませんでした。10万ドル程度までは、この範囲が適切だと思います。
この疑問から、私は特定の計算式を作成しました。これは1200ドルから数百万ドルまでのあらゆるジャックポットに当てはまると思います。以下がその計算式です。
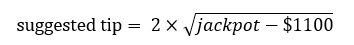
画像が見えない場合は、2×sqrt(ジャックポット-$1100)となります。
一般的なジャックポットの金額を計算する式は次のとおりです。
提案チップ表
| ジャックポット | ヒント |
|---|---|
| 1,200ドル | 20ドル |
| 2,000ドル | 60ドル |
| 5,000ドル | 125ドル |
| 1万ドル | 189ドル |
| 2万ドル | 275ドル |
| 5万ドル | 442ドル |
| 10万ドル | 629ドル |
| 100万ドル | 1,999ドル |
110万ドルの場合、私の計算式では2,096.57ドルと算出されます。2,000ドルに切り捨てても大丈夫だと思います。もちろん、サービスの質など、他の要素も考慮してください。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
任意の大きな数について、その数の近くにある素数間の平均距離はどれくらいでしょうか?また、その数より小さい素数はいくつあるでしょうか?
任意の大きな数nの近傍における素数間の平均距離の非常に良い推定値はln(n)です。この推定値の精度の高さは注目に値します。
証拠として、次の表は最初の1500万個の素数の範囲を100万個ずつのグループに分けて示しています。表は、素数間の範囲内の平均距離と、平均距離の推定値を示しています。推定値は、範囲内の最大素数と最小素数の平均の自然対数です。例えば、15番目の100万個の素数グループの場合、ln((256,203,221+275,604,541)/2)となります。
素数間の平均距離
| ファーストプライム 範囲内 | ラストプライム 範囲内 | 素数 範囲内 | 平均距離 | 見積もり | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | 1,000,000 | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | 1,000,000 | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | 1,000,000 | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | 1,000,000 | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | 1,000,000 | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | 1,000,000 | 18.367144 | 18.3716137 | |
| 104,395,303 | 1億2294万9823 | 1,000,000 | 18.55452 | 18.54883262 | |
| 1億2294万9829円 | 1億4165万939円 | 1,000,000 | 18.70111 | 18.70058553 | |
| 1億4165万9630円 | 1億6048万1183 | 1,000,000 | 18.83022 | 18.83322787 | |
| 1億6048万1219円 | 1億7942万4673 | 1,000,000 | 18.943454 | 18.95103217 | |
| 1億7942万4691 | 1億9849万1317円 | 1,000,000 | 19.066626 | 19.05703535 | |
| 1億9849万1329円 | 2億1764万5177円 | 1,000,000 | 19.153848 | 19.15337672 | |
| 2億1764万5199円 | 2億3,688万7,691 | 1,000,000 | 19.242492 | 19.24163365 | |
| 2億3,688万7,699 | 2億5,620万3,161 | 1,000,000 | 19.315462 | 19.32305683 | |
| 2億5,620万3,221 | 2億7560万4541 | 1,000,000 | 19.40132 | 19.39864545 |
出典: Prime Pages のThe Gaps Between Primes 。
任意の数における素数の個数を求めるには、まず平均距離の推定値ln(n)を積分することから始めます。これにより、任意の数nまでの素数間の平均距離の合計が得られます。
f(n)=ln(n)の積分はいくらでしょうか?部分積分から次のことがわかります。
f(n)*g'(n) dnの積分 = f(n)*g(n) - (f'(n)*g(n)) dnの積分
f(n)=ln(n)、g'(n)=1とします。すると、f'(n)=1/n、g(n)=nとなります。したがって、ln(n)の積分は、ln(n)*n - ((1/n)*n)の積分 = ln(n)*n - n = n*(ln(n)-1)となります。
n*(ln(n)-1)をnで割ると、2からnまでの範囲における素数間の平均距離が得られます。これはln(n)-1です。
n をこの素数間の平均距離で割ると、n 未満の素数の平均数が得られ、これは n/(ln(n)-1) に等しくなります。
証拠として、以下の表は様々な大きな数における素数の個数と推定値を示しています。Excelの精度は15桁までしかなく、ご容赦ください。誰か、もっと高い精度に対応できるスプレッドシートを作ってください。
素数間の平均距離
| n | n以下の素数 | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1,000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 10万 | 9,592 | 9,512 |
| 1,000,000 | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 1億 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 4億5,505万2,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
出典: Prime Pages の「素数はいくつあるか? 」


