Wizardに尋ねる #353
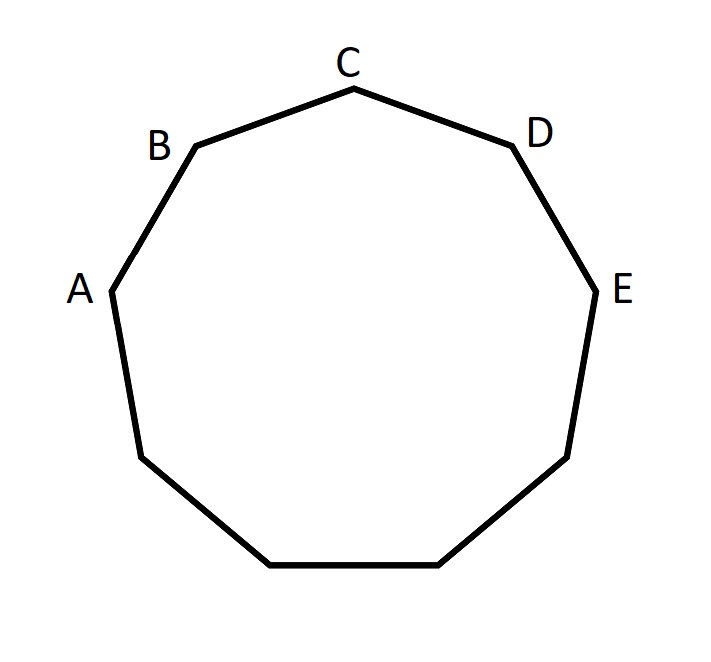
上の図は、辺の長さが 1 の九角形です。
AB+AC と AE ではどちらが多いでしょうか?
この問題はMensa Bulletin 2021 年 3 月号から抜粋したものです。
この問題に対する私の解決策は次のとおりです。(PDF)
答えが整数であると仮定して、3 桁または 4 桁の数字の平方根を簡単に求めるにはどうすればよいでしょうか。
次の表は、0 から 9 までの数字、それぞれの数字の平方、およびその平方の最後の桁を示しています。
平方数の最後の桁
| オリジナル 番号 | 四角 | 最後の桁 スクエアの |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
偶数平方の数は必ず0、1、4、5、6、または9で終わることに注意してください。これはすべての平方数に当てはまります。これは、元の数の最後の桁が平方数の最後の桁を決定するためです。
ステップ1:平方根の最後の桁に基づいて、以下の表を使って平方根の最後の桁を絞り込むことができます。例えば、平方根が2809の場合、平方根の最後の桁は3または7です。
元の番号の最後の桁
| 最後の桁 平方根の | 最後の桁 スクエアの |
|---|---|
| 0 | 0 |
| 1 | 1または9 |
| 4 | 2または8 |
| 5 | 5 |
| 6 | 4または6 |
| 9 | 3または7 |
ステップ2:次に、元の数字の右2桁を切り捨てます。例えば、元の数字が2809だった場合は、28を使用します。
ステップ3:ステップ2の結果以下の最小の平方数を見つけます。そして、その平方数の平方根を取ります。例えば、28より小さい最小の平方数は25です。25の平方根を取ると5になります。
100 までの平方数を記憶していない場合は、次の表を使用できます。
平方根の最初の部分
| ステップ2 | ステップ3 |
|---|---|
| 1から3 | 1 |
| 4~8 | 2 |
| 9~15歳 | 3 |
| 16~24歳 | 4 |
| 25~35歳 | 5 |
| 36から48 | 6 |
| 49から63 | 7 |
| 64から80 | 8 |
| 81から99 | 9 |
ステップ 4: ステップ 1 の結果が 0 または 5 の場合は、それをステップ 3 の結果の後に置いて完了です。
それ以外の場合、a = ステップ3の結果とします。b = a×(a+1)とします。例えば、ステップ3の結果が5の場合、b = 5×6 = 30となります。
ステップ 5: b < a の場合、平方根の最後の桁はステップ 1 で得られた可能性のうち小さい方になります。それ以外の場合、b >= a の場合は、2 つの可能性のうち大きい方になります。
ステップ 6: 平方根を求めるには、ステップ 3 の結果を取得し、それにステップ 5 の結果を加算します。つまり、10 × (ステップ 3) + ステップ 5 となります。
いくつかの例を見てみましょう。
256 の平方根を求めます。
- ステップ 1: 平方根の最後の桁は 4 または 6 です。
- ステップ 2: 最後の 2 桁を削除すると、2 になります。
- ステップ 3: 2 以下の最小の平方数は 1 です。1 の平方根は 1 です。
- ステップ4: 1*(1+1) = 2。
- ステップ 5: ステップ 4 の結果はステップ 2 の結果と等しいので、ステップ 1 のオプションのうち大きい方を最後の桁、つまり 6 として使用します。
- ステップ 6: 平方根は、ステップ 5 の結果を 3 の結果に加算したもので、1 & 6 = 16 になります。
1369 の平方根を求めます。
- ステップ 1: 平方根の最後の桁は 3 または 7 です。
- ステップ 2: 最後の 2 桁を削除すると、13 になります。
- ステップ 3: 13 以下の最小の平方数は 9 です。9 の平方根は 3 です。
- ステップ4: 3*(1+3) = 12。
- ステップ 5: ステップ 2 の結果はステップ 4 の結果よりも大きいため、ステップ 1 のオプションのうち大きい方を最後の数字として使用します (つまり、7)。
- ステップ 6: 平方根は、ステップ 5 の結果を 3 に加えた結果であり、3 & 7 = 37 になります。
2704 の平方根を求めます。
- ステップ 1: 平方根の最後の桁は 2 または 8 です。
- ステップ 2: 最後の 2 桁を削除すると、27 になります。
- ステップ 3: 27 以下の最小の平方数は 25 です。25 の平方根は 5 です。
- ステップ4: 5*(1+5) = 60。
- ステップ 5: ステップ 2 の結果はステップ 4 の結果より小さいため、ステップ 1 のオプションのうち小さい方を最後の桁として、つまり 2 を使用します。
- ステップ 6: 平方根は、ステップ 5 の結果を 3 の結果に加算したもので、5 & 2 = 52 になります。
5625 の平方根を求めます。
- ステップ 1: 平方根の最後の桁は 5 です。
- ステップ 2: 最後の 2 桁を削除すると、56 になります。
- ステップ 3: 56 以下の最小の平方数は 49 です。49 の平方根は 7 です。
- ステップ4: ステップ1の結果は0または5なので、答えはステップ3の結果にステップ1の結果を加えたものになります: 7 & 5 = 75
6561 の平方根を求めます。
- ステップ 1: 最後の数字は 1 または 9 です。
- ステップ 2: 最後の 2 桁を削除すると、65 になります。
- ステップ 3: 65 以下の最小の平方数は 64 です。64 の平方根は 8 です。
- ステップ4: 8*(1+8) = 72。
- ステップ 5: ステップ 2 の結果はステップ 4 の結果より小さいため、ステップ 1 のオプションのうち小さい方を最後の桁、つまり 1 として使用します。
- ステップ 6: 平方根は、ステップ 5 の結果を 3 の結果に加算したもので、8 & 1 = 81 になります。
この方法のデモはYouTubeでご覧いただけます。
ブラックジャックを 12 時間プレイした場合、60 回以上連続して勝つ確率はどれくらいでしょうか?
私のブラックジャックの分散のページによると、リベラルなストリップルールに基づく、純勝ち、プッシュ、または負けの確率は次のとおりです。
- 勝利 — 42.43%
- プッシュ — 8.48%
- 損失 — 49.09%
引き分けを無視して、ハンドが純粋な勝ちまたは負けで解決された場合の勝利の確率は 46.36% になります。
プレイ速度として、1時間あたり100ハンドを使用しましょう。
少なくとも 60 ハンド連続で少なくとも 1 回の連続が発生する確率は次のように概算できます。
100×12×0.4636 60 = 89,412,355,233,588,500分の1。比較の基準として、パワーボールとメガミリオンズのチケットを 1 枚ずつ購入した場合、両方が当たる確率は 88,412,922,115,818,300 分の 1 になります。
したがって、12 時間のプレイで 60 回連続で勝つよりも、両方の宝くじに当たる可能性の方が少し高くなります。


