Wizardに尋ねる #355
映画『消されたライセンス』で、ジェームズ・ボンドはブラックジャックを3ラウンドプレイし、一度に5ハンドをプレイします。彼は一度もヒットしなかったようです。その確率はどれくらいでしょうか?
そのシーンのクリップはYouTubeで見つかります。
このゲームでは、大きなカードが驚くほど多く登場しますね。私が確認できたカードは以下の通りです。ただし、カードによってははっきりと見えない場合もあるのでご了承ください。
殺害許可証 -- 観察された階級
| ランク | 観察された |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| J | 3 |
| 質問 | 6 |
| K | 4 |
| あ | 1 |
| 合計 | 35 |
確かにその通りです。ボンドは最初の15ハンドで一度もヒットしていません。8を一度スプリットしましたが、その後もヒットしていません。15ハンド全てにおける彼の最初のアクションは以下の通りです。
- ダブル — 1
- 分割 — 1
- スタンド — 13
ここでは、6 つのデッキがあり、スプリット後にダブルが許可され、ディーラーがホールカードを覗き、ディーラーがソフト 17 でスタンドすることを前提とした、各初期アクションの基本戦略の確率を示します。
ブラックジャック -- 最初のアクションの確率
| アクション | 確率 |
|---|---|
| 立つ | 43.46% |
| 打つ | 39.78% |
| ダブル | 9.53% |
| スプリット | 2.48% |
| ブラックジャック | 4.75% |
| 合計 | 100.00% |
降伏が認められた場合、その確率は立つ確率から 4.14% になります。
ボンドは16対10で一度スタンドしたことに注目すべきです。基本戦略としては、その状況でヒットするのが基本戦略ですが、非常に微妙です。そのハンドで10が大量に出たことから、ボンドはカウントが高いことを知っていた可能性があり、その状況でスタンドすることで基本戦略の例外が発動する可能性があります。
いずれの手もヒットしない確率は60.22%です。各手が独立していると仮定した場合、15回中15回ヒットしない確率は、2015年に0.602162 15 = 0.000496253 = 約1となります。
「イカゲーム」では、16人のプレイヤーがガラスの橋を使ってゲームをします。橋は18組のガラスに分かれており、各組のガラスのうち1枚は強化ガラスで、プレイヤーの体重を支えることができます。もう1枚は通常のガラスで、プレイヤーの体重で割れてしまいます。プレイヤーが通常のガラスを踏むと、ガラスが割れて落下し、死んでしまいます。
プレイヤーは、あらかじめ決められた順番で、一人ずつ前進しなければなりません。
それぞれのガラスの階段でランダムに推測すると仮定すると、安全に渡れるプレイヤーの予想数はどれくらいでしょうか?
世界中の人々が自分で答えを導き出す楽しみを味わえるよう、答えと解決方法をネタバレタグで付けておきます。
プレイヤー1が安全に渡る確率は、(1/2)^18 = 1/262144 = 約0.000004です。
プレイヤー 2 が安全に渡るには 2 つの方法があります。
- プレイヤー1は安全に渡りました。この場合、プレイヤー2は彼のステップをそのまま真似すれば良いのです。
- プレイヤー1とプレイヤー2の間には、悪いステップが1つだけあります。これは、ガラスのペアの18組のうちの18組で発生する可能性があります。17組の正しいステップと1組の悪いステップの確率は、18*(1/2)^2 = 18/262144 = 0.000069です。
したがって、プレイヤー 2 が安全に渡る確率は、0.000004 + 0.000069 = 0.000072 です。
プレイヤー 3 が安全に渡るには 2 つの方法があります。
- プレイヤー2は安全に渡りました。この場合、プレイヤー3は彼のステップをそのまま真似すれば良いのです。
- プレイヤー1、2、3の間では、悪いステップは2つだけです。プレイヤー1と2を倒す2つのピースについて、18組のガラスの中から2つを選ぶ方法は、combin(18,2)=153通りあります。16回の良いステップと2回の悪いステップの確率は、153*(1/2)^2 = 153/262144 = 0.000584です。
したがって、プレイヤー 3 が安全に渡る確率は 0.000072 + 0.000584 = 0.000656 です。
プレイヤー 4 が安全に渡る方法は 2 つあります。
- プレイヤー3は安全に渡りました。この場合、プレイヤー4は彼のステップをそのまま真似すれば良いのです。
- プレイヤー1から4の間では、悪いステップは3つだけです。プレイヤー1から3を倒す2つのピースについて、18組のガラスの中から3つを選ぶ方法は、combin(18,3)=816通りあります。15回の良いステップと3回の悪いステップの確率は、816*(1/2)^2 = 816/262144 = 0.003113です。
このロジックに従うと、各プレーヤーの確率の次の表が得られます。
ブリッジゲーム
| プレーヤー | 確率 生存 |
|---|---|
| 1 | 0.000004 |
| 2 | 0.000072 |
| 3 | 0.000656 |
| 4 | 0.003769 |
| 5 | 0.015442 |
| 6 | 0.048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0.407265 |
| 10 | 0.592735 |
| 11 | 0.759659 |
| 12 | 0.881058 |
| 13 | 0.951874 |
| 14 | 0.984558 |
| 15 | 0.996231 |
| 16 | 0.999344 |
| 合計 | 7.000076 |
答えを閉じた形で表現すると、次のようになります。
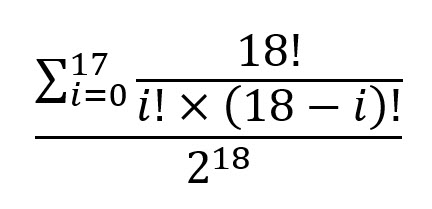
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
Ultimate X Goldでは、3:10の時点で、3が4の上に重ねられた、パットフルハウスが配られました。2から4までのフォーカードのマルチプライヤーは9倍でした。フルハウスのマルチプライヤーは1倍でした。なぜ、3が3つだけ揃うのではなく、パットフルハウスをキープして、マルチプライヤーの高いフォーカードを目指すのですか?
君の言う通りだ、その手で完全に失敗したよ。
10プレイをしていたことを思い出してください。つまり、フルハウスで勝った場合の配当は10×35 = 350でした。
3 だけを保持している場合、各ハンドには次の確率があります。
- フォー・オブ・ア・カインド — 4.26%
- フルハウス — 6.11%
- スリーオブアカインド — 89.64%
乗数適用後の各ハンドの勝利は次のとおりです。
- フォー・オブ・ア・カインド — 1800
- フルハウス — 35
- スリー・オブ・ア・カインド — 15
3のカードだけを持っていたとしたら、期待リターンは(4.26% * 1800) + (6.11% * 35) + (89.64% * 15) = 92.17854でした。これはフルハウスの35を大きく上回ります。つまり、このハンドで私は恥ずかしいミスを犯したのです。
ある人が私にこんな賭けを挑んできました。標準的なポーカーデッキから3つの数字を選び、予想を書きますが、最後まで伏せておきます。例えば、7-エース-2。すると彼は、もし3つ当てられたら、少なくとも1つの数字を当てられると賭け金を同額にすると申し出てきました。私の勝率はどれくらいでしょうか?
勝つには、相手が3つの予想をすべて間違える必要があります。最初の予想が間違っている確率は10/13です。2番目の予想が間違っている確率は9/12です。これは、最初のランクを可能性として推測した可能性を除外できるためです。3番目の予想が間違っている確率は8/11です。これは、最初の2つのランクを可能性として推測した可能性を除外できるためです。
勝つには、これら3つの条件がすべて満たされる必要があります。したがって、勝つ確率は(10/13) * (9/12) * (8/11) = 720/1716 = 41.96%となります。
均等な金額の場合、この賭けのあなたの側のハウスエッジは 16.08% です (痛い!)。
この質問は、Owen E'Shea 著の The Book of Proposition Bets (番号 7) から抜粋されました。


