Wizardに尋ねる #367
クラップスではすべての数字に賭けるのが好きです。7アウトになる前に、いくつの異なる数字が当たると予想できますか?
他の読者のために、質問は、合計が 7 になる前に 2 つのサイコロを振って次の合計のうちいくつが出るかを尋ねています: 4、5、6、8、9、10。
答えは2.375758です。以下の表は、指定された範囲で0から6までの異なる合計が出る可能性ごとの確率を示しています。右下のセルは、7が出るまでの平均の異なる合計を示しています。
ユニークな数字が出た
| 合計 | 確率 | 期待される |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| 合計 | 1.000000 | 2.375758 |
公平なコインを投げると、表向きに出た面が表向きになる確率が高くなるというのは本当ですか?
証拠はこれが真実であることを示しています!
スタンフォード大学のペルシ・ディアコニスとスーザン・ホームズは、1万回のコイン投げを記録しました。コインは50.8%の確率で、投げたときと同じ面を上にして着地しました(出典:アメリカ数学会のニュースレター「What's Happening in the Mathematical Sciences」に掲載されている 「The Fifty-one Percent Solution 」)。この比率以上になる確率は5.48%です。
これを数学的に証明するために、コインの実際の回転数はポアソン分布に従うと仮定しました。より具体的には、平均回転数がmの場合、ちょうどn回回転する確率はexp(-m)*m^n/n!です。ポアソン分布を説明するために、次のグラフは平均10が与えられた場合に、0から25回回転する確率を示しています。
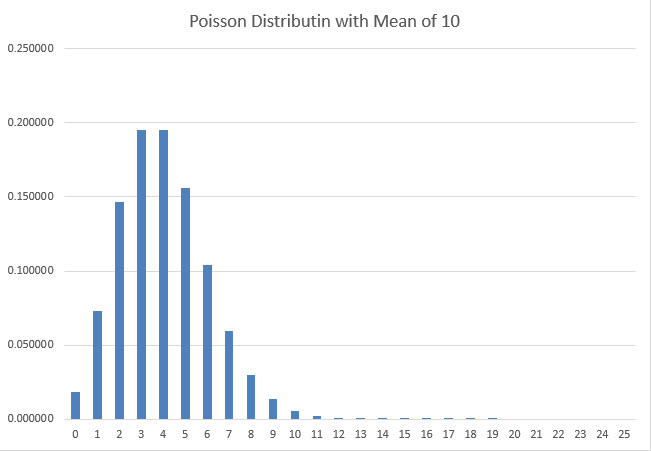
私がポアソン仮定を選択した理由は、十分に大きな平均値に対してほぼベル曲線の形状に従い、実際の結果がゼロを下回ることはないからです。
次に、半回転の回数が偶数回(開始時と同じ面が上を向いて着地する)となる確率を、様々な半回転の平均について計算しました。以下の表は、平均0.5~5.0の場合の結果を示しています。
偶数回転と奇数回転の確率
| ミーン・レボリューションズ | 合計 | 奇数合計 |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
そこで、なぜ偶数の確率が常に50%より大きいのか疑問に思いました。平均mが与えられた場合、偶数の確率は0.5 + e^(-2m)/2と表されることがわかりました。eのべき乗は必ず正の値となるため、回転回数が偶数となる確率も正となります。
この式の証明はここで見ることができます。
「ザ・プライス・イズ・ライト」のスペリングビーゲームについての分析を教えてください。
他の読者のために、まずルールについて説明させてください。
- 1 から 30 までの番号が付けられた 30 枚のカードが入ったボードがあります。
- 各カードの裏面には「car」という文字または単語が書かれています。それぞれの配置は以下のとおりです。
- C: 11
- 答え:11
- レート: 6
- 車: 2台
- ホストはプレイヤーに 2 枚のカードを選ばせます。
- 価格決定ゲーム(これについてはここでは触れません)の後、プレイヤーはさらに最大 3 枚のカードを得るチャンスがあります。
- カードは裏返されます。
- プレイヤーは 2 つの方法のいずれかで車を獲得できます。
- プレイヤーは各文字のカードを少なくとも 1 枚受け取ります (つまり、CAR という単語が綴られます)。
- プレイヤーは「CAR」カードを少なくとも 1 枚受け取ります。
- ゲームのどの時点でも、プレイヤーは降参して、めくられていないカードごとに 1,000 ドルを受け取ることができます。
ゲームのプレイ中のクリップはこちらです。
次の表は、まだカードがめくられていないと仮定して、プレイヤーが持っているカードの枚数に応じた勝利の確率を示しています。
スペリングビー — 優勝確率
| カード | 確率 勝利 |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
カードがめくられる前に、プレイヤーは車の価値が妥当であると仮定し、降参すべきではありません。例えば、カードが2枚しかない場合でも、プレイヤーが少なくとも1枚の「CAR」カードを持っている確率は13.1%です。もし車の価値が15,263.16ドルだった場合、プレイヤーは2,000ドルの降参金には無関心であるべきです。どんな新車でも、その価値はそれ以上になるでしょう。
以下は、プレイヤーが持っている未めくりのカードの枚数に応じた、車の価値に対する無差別ポイントです。
スペリングビー — 優勝確率
| カード | 無関心 ポイント |
|---|---|
| 2 | 15,263.16ドル |
| 3 | 8,066.23ドル |
| 4 | 6,849.11ドル |
| 5 | 6,803.75ドル |


