Wizardに尋ねる #373
きっとあなたは『ビッグバン★セオリー』のファンでしょう。私のお気に入りのシーンの一つは、トカゲとスポックのじゃんけんです。5つのシンボルを使ったじゃんけんのようなもので、ルールは以下のとおりです。
- 紙は岩を覆う
- 岩がトカゲを押しつぶす
- トカゲがスポックに毒を盛る
- スポックがハサミを叩き壊す
- はさみは紙を切る
- トカゲが紙を食べる スポックは岩を蒸発させる
- はさみがトカゲの首を切る
- 論文はスポックの反証となる
- 岩がハサミを粉砕する
私の質問は、ランダムなプレイヤーに対してすべての側が同じチャンスを持つように、さらにシンボルを追加できるかどうかです。
はい、私もそのシーンが大好きです! YouTube動画はこちらです。
シンボルの数は奇数である必要があります。理論上は偶数でも構いませんが、その場合、特定のシンボルの組み合わせで引き分けになるようなルールを設けなければなりません。いいえ、両プレイヤーが同じシンボルをプレイした場合にのみ引き分けとなる、決定的なゲームを目指しています。
素数の記号を使うと、特にエレガントで簡単に説明できる解決策があります。例として、7つの記号を使って説明しましょう。次の図のように、記号AからGにラベルを付け、円上に表してみましょう。
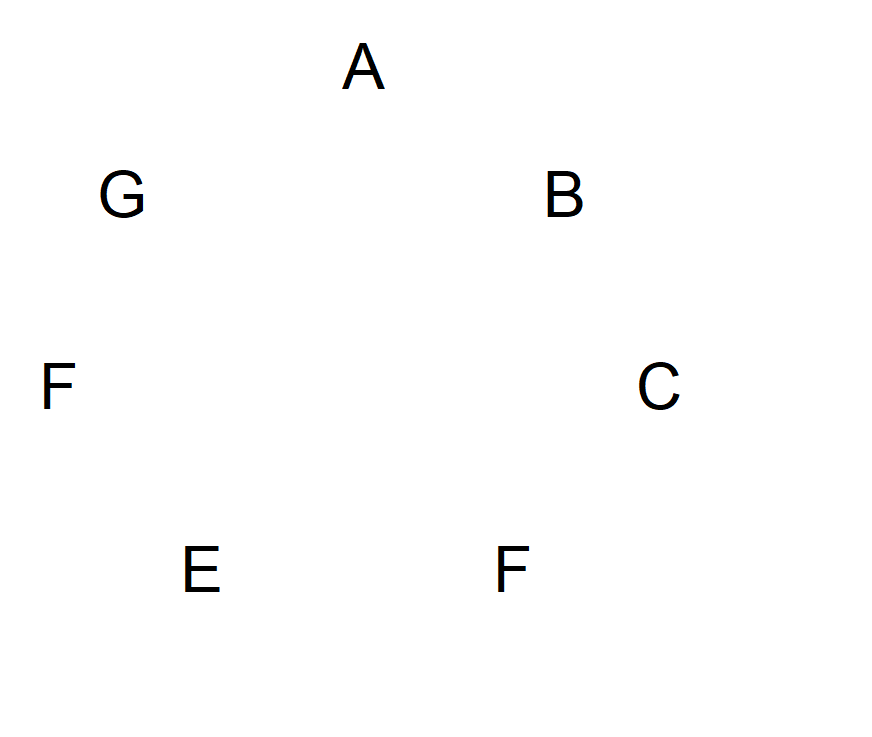
次に、Aから始めて時計回りに次の記号まで矢印を描きます。矢印は、この2つの記号のどちらかに向かいます。まるで、その記号に矢が放たれているかのように考えてください。Aに戻るまで時計回りに描き続けます。図は次のようになります。
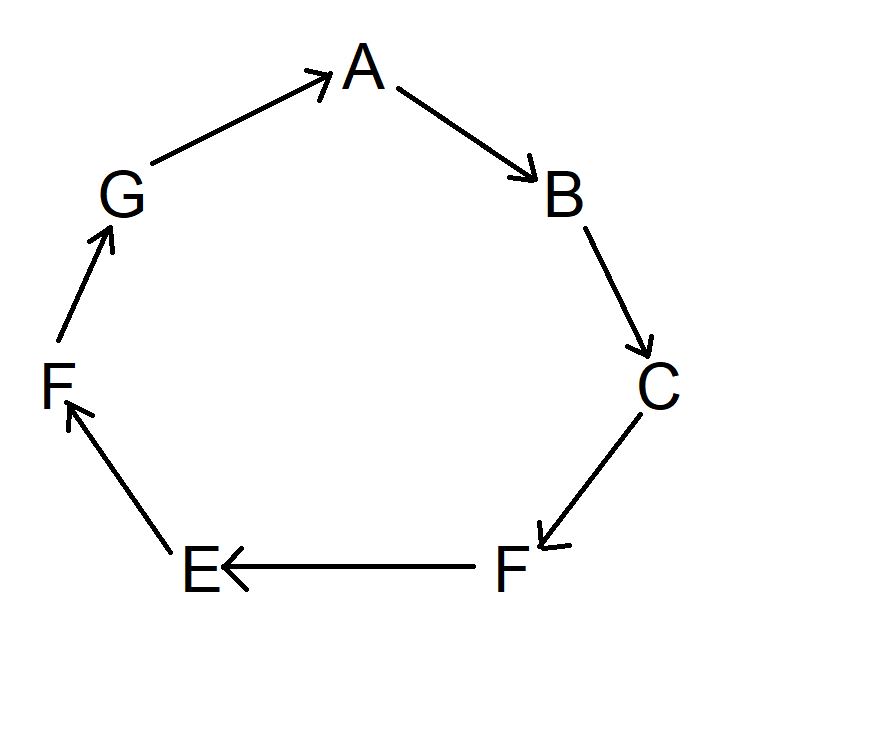
次に、同じことをAから始めて、時計回りに2つずつ記号を進めます。実際には、どこから始めても構いません。図は次のようになります。
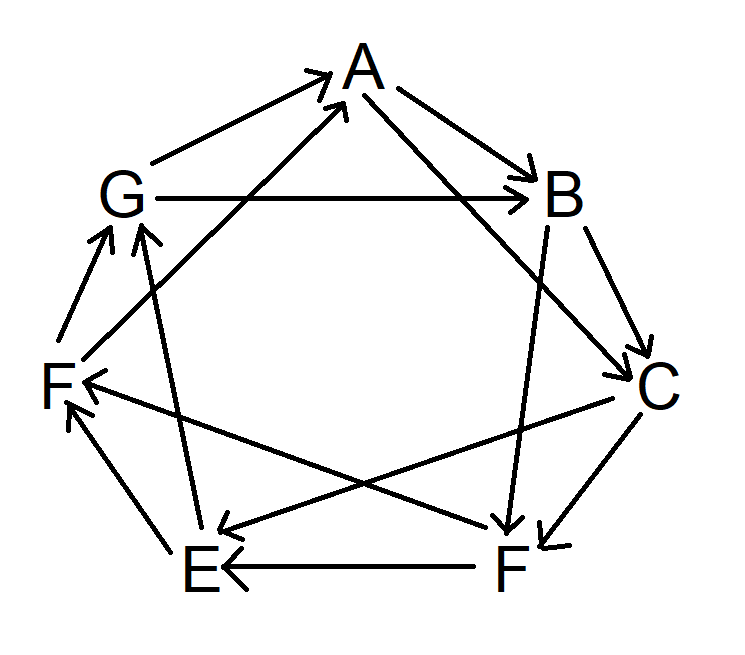
最後に、同じことを時計回りに3つの記号を飛ばして行います。図は次のようになります。
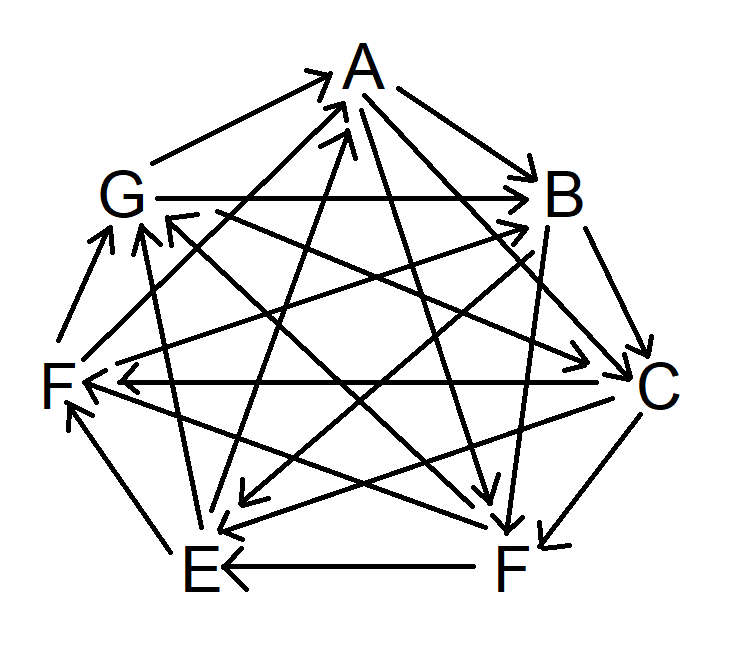
この時点で、すべてのシンボルが他の 3 つのシンボルに勝ち、他の 3 つの異なるシンボルに負けていることに注意してください。
この方法は、元の記号に戻るまでにすべての記号を通過しているため、素数の記号に対しても有効です。n個の記号の場合、このプロセスを(n-1)/2回繰り返す必要があります。
奇数個のシンボルでもバランスの取れたゲームを作ることはできますが、元のシンボルに早く戻ってしまうことがあります。そうなると、見逃したシンボルからもう一度ループを組む必要があります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
スリーカードポーカーで引き分けになる確率はどれくらいですか?
正確な答えは 450528/407170400 =~ 0.001106485 =~ 1/904 です。
以下の表は、各タイプの最初のハンドを作る方法の数と、2番目のハンドで同点になる組み合わせの数を示しています。ストレートやトラッシュハンドの場合、最初のハンドに2つのスーツが含まれているか、3つのスーツが含まれているかが重要になります。
右下のセルは、スリーカードポーカーでタイになる組み合わせが450,528通りあることを示しています。2つのハンドの組み合わせの合計は、combin(52,3)*combin(49,3) = 407170400です。したがって、答えは450528/407170400です。
スリーカードポーカーの引き分け
| 手 | 手1 | ハンド2 | 製品 |
|---|---|---|---|
| スリーオブアカインド | 52 | 0 | 0 |
| ストレートフラッシュ | 48 | 3 | 144 |
| ストレート(3つのスーツ) | 288 | 26 | 7,488 |
| ストレート(2つのスーツ) | 432 | 25 | 10,800 |
| フラッシュ | 1,096 | 3 | 3,288 |
| ペア | 3,744 | 3 | 11,232 |
| ジャンク(3つのスーツ) | 6,576 | 26 | 170,976 |
| ジャンク(2つのスーツ) | 9,864 | 25 | 246,600 |
| 合計 | 22,100 | 450,528 |
6-5 ブラックジャックにおける無料エース クーポンの価値はいくらですか?
私のフリー エースの価値のページでは、その価値は 3-2 ブラックジャックの賭け金の 50.1844% であると述べています。
6デッキのブラックジャックでは、最初のカードがエースの場合、ブラックジャックが勝つ確率は29.3139%です。この場合、6-5ブラックジャックでは3-2ブラックジャックよりも0.3ユニット少なくなります。
したがって、6-5 6 デッキ ブラックジャックでのフリー エースの価値は、初期ベットの 50.1844% × 29.3139 × 0.3 = 41.3902% になります。
ある人が私に賭けを挑んできました。彼が27回振って、2つのサイコロの合計が12になるかどうかです。もし彼が12が出なければ、私は同額の賞金を獲得します。12が出る確率は1/36なので、彼が12を出すには平均36回振る必要があるのではないでしょうか?もし相手が27回しか出なかったら、私の方が有利になるように見えます。私の計算は正しいでしょうか?それとも私の計算のどこかに間違いがあるのでしょうか?
12が出るまでの平均的な待ち時間は、12が出るまでの時間を含めて36回です。しかし、これは36回投げるたびに12が出るという意味ではありません。12が出ない確率は(35/36)です。27回投げて12が出ない確率は(35/36)の27乗です。つまり、少なくとも1回12が出る確率は1-(35/36)の27乗=53.26%です。
以下の表は、20回から36回ロールした際に、少なくとも12が出る確率を示しています。ただし、イーブンマネーで有利になるには25回必要であることに注意してください。
確率12
| ロール | 確率 |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |


