Wizardに尋ねる #375
コンシューマー・レポートは、タイヤのローテーションを行えばタイヤ代を節約できると主張しています。ほとんどの車が前輪駆動車であるため、片方のタイヤは約2万マイル、後輪は約6万マイルの寿命があると彼らは主張しています。また、タイヤを頻繁にローテーションすれば、約4万マイルも長持ちするとも述べています。
とはいえ、あるドライバーがタイヤローテーションを行わない場合、12万マイル走行すると、前輪6組、後輪2組、合計2×(2+6)=16本のタイヤが交換されることになります。一方、別のドライバーがタイヤローテーションを行う場合、4本×3組、合計12本のタイヤが交換されます。
何か怪しいですね。タイヤの摩擦力は、ローテーションの有無に関わらず、1マイルあたりで同じではないでしょうか?タイヤをローテーションさせることの安全上のメリットを否定はしませんが、ローテーションさせるとなぜタイヤの摩耗が魔法のように遅くなるのでしょうか?
いい質問ですね。コンシューマー・レポートが提示した仮定に基づくあなたの計算には同意します。しかし、彼らの仮定には同意できません。彼らは怠慢で、ローテーションタイヤの寿命を算出する際に前輪と後輪の平均寿命を基準にしてしまったように思います。
例えば、4本のタイヤを新品で走行したドライバーを考えてみましょう。15,000マイル走行後、前輪と後輪を交換します。交換前は、前輪のトレッドは75%、後輪は25%摩耗していました。交換後は、前輪のトレッドは75%、後輪は25%残ります。その後、さらに15,000マイル走行します。ここでも、新品タイヤと比較して前輪は75%、後輪は25%摩耗します。つまり、30,000マイル走行後には、両方のタイヤのトレッドが0になります。コンシューマー・レポートが主張する40,000マイルではありません。
ローテーションによる正確な寿命を求めるには、トレッド摩耗の平均値をとる必要があります。今回の場合は、1/20,000と1/60,000を平均して1/30,000とします。次に、この1マイルあたりの平均摩耗量の逆数を取ることで、ローテーション後のタイヤの寿命を算出します。これは30,000です。あるいは、2*F*R/(F+R)という式を使うこともできます。ここで、Fは前輪の寿命、Rは後輪の寿命です。
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
52 枚のカードの組み合わせは combin(52,5) = 2,598,960 通りあることが分かっています。私の質問は、5 デッキのシューから 5 枚のカードで何通りのハンドが考えられますか?
一度に 1 つのタイプの手を取り上げてみましょう。
- 同じカードが 5 枚: デッキには 52 種類のカードがあり、52 通りの組み合わせがあります。
- 同じカードが4枚:同じカードが4枚ある場合、その組み合わせは52通り、1枚しかない場合、51通りあります。つまり、フォー・オブ・ア・カインドの組み合わせは52×51=2,652通りあります。
- 同じカードが3枚と、別のカードが2枚の場合:同じカードが3枚の場合は52通り、ペアの場合は51通りあります。つまり、フルハウスの組み合わせは52×51=2,652通りあります。
- 同じカードが3枚と、異なるシングルトンが2枚の場合:同じカード3枚の組み合わせは52通り、シングルトン2枚の組み合わせはcombin(51,2)=1,275通りあります。つまり、スリーカードの組み合わせは52*1,275=66,300通りあります。
- 同じカードが2組ペアになり、シングルトンが1枚ある場合:ペアとなる2枚の異なるカードの組み合わせは、combin(52,2)=1,326通りあります。そして、シングルトンは50通り残ります。つまり、ツーペアとなる組み合わせは1,326*50=66,300通りあります。
- 同じカードが1組とシングルトンが3枚の場合:ペアのカードは52通りあります。残りのシングルトン51枚から3枚を選ぶ方法は、combin(51,3)=20,825通りあります。つまり、ペアの組み合わせは52*20,825=1,082,900通りです。
- 5 つのシングルトン: 52 枚の中から 5 枚のカードを選択する方法は combin(52,5)=2,598,960 通りあります。
これらの組み合わせの合計は 3,819,816 です。
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
正方形と円を含む次の図を考えてみましょう。
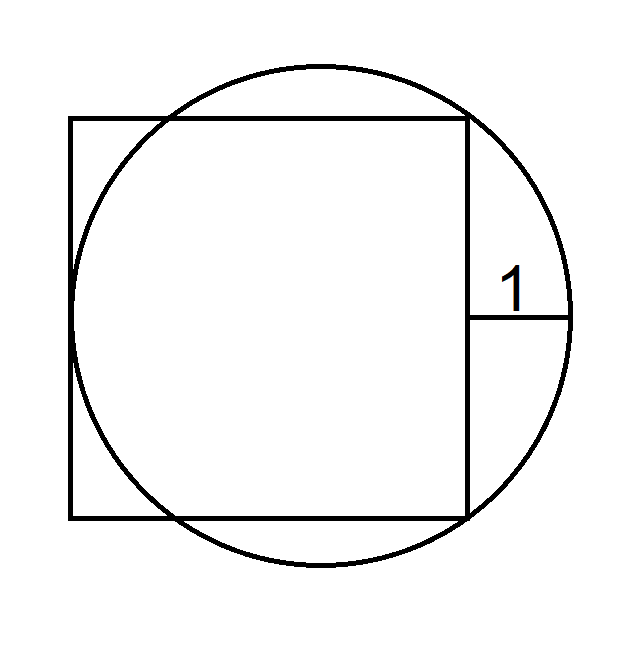
正方形の面積はいくらですか?