Wizardに尋ねる #377
3つの会社が、それぞれ異なる程度の欠陥を持つ製品を製造しているとします。具体的には、3社全てにおいて、欠陥のない製品を製造できる割合は以下のとおりです。
- アクメ:85%
- ブラウン:90%
- 魅力: 95%
ウィジェットを販売している店舗は、Delta、Theta、Omegaの3つです。店舗とメーカーの間には1対1の関係があるようですが、それが何なのかは分かりません。
3 つの店舗をランダムにサンプリングすると、次の結果が得られます。
テストデータ
| 店 | 効果的 | 欠陥品 |
|---|---|---|
| デルタ | 10 | 0 |
| シータ | 48 | 2 |
| オメガ | 186 | 14 |
効果的なウィジェットを購入することがあなたの目標です。どのストアから購入すべきでしょうか?各ストアの有効性はどの程度でしょうか?
ストア B から購入する必要があります。各ストアからの有効なウィジェットの確率は次のとおりです。
- デルタ: 91.76%
- シータ: 93.57%
- オメガ:92.91%
ロビー・ジェイド対ギャレット・アデルスタインのポーカーハンドについてどう思いますか?ロビーは不正行為をしたのでしょうか?
このテーマはネット上で徹底的に分析されていますが、私の側に立つ人はあまりいないと思うので、私も賛同したいと思います。
私はロビー・ジェイドの味方です。
長い話を短くまとめると、二人はフィル・アイビーをはじめとするポーカー界の大物たちとテレビ中継されたポーカーゲームに出場していました。要約すると、二人とも弱いハンドでした。ギャレット・アデルスタインが大きなベットをし、ロビー・ジェイドがコールしました。ポーカーはギャンブルに関しては私の苦手分野ですが、弱いハンドの場合は一般的にアグレッシブにベットするかフォールドするかのどちらかであることは私でも理解しています。コールはしません。まさに教科書通りのポーカーです。
長い話を短くまとめると、ロビーは型破りなプレイで勝利しました。前述の通り、このトーナメントはテレビ中継され、ホールカードリーダーもいました。勝利後、ギャレットはロビーが不正行為をしたと非難しました。おそらく彼の主張は、ロビーが放送中の誰かと共謀し、相手のカードをシグナルで受け取ったというものでしょう。
ロビーは番組で、ホールカードがJ/3だと勘違いしていたと説明しましたが、実際にはJ/4でした。3なら少なくともボードはペアになります。
ゲームの後半、彼女は舞台裏で、ギャレットがハンドで失った13万5000ドルを返した。理由は、二人の間にドラマチックな出来事やわだかまりが生じたくなかったからだと語った。
彼女がなぜお金を返したのか、いまだに理解できません。陰謀論者は、彼女が不正行為をしたことを認めたのだと言います。しかし、不正行為をした人が事後に罪悪感を感じてお金を返すことはあまりないと思います。争いを避け、非難されないために、善良な人が正当に稼いだお金を手放す方が一般的だと思います。
話にはもっと細かい点があるが、ここでは触れない。要するに、ギャレットはそのハンドで正々堂々と負けたということだ。運と技術が絡むゲームでは、弱いプレイヤーが勝つこともある。ポーカープレイヤーなら誰でも、何千回もそれを目にしてきたはずだ。
こちらはゲームのクリップです。
関連する瞬間:
- 2:07:24~2:24:16 -- 問題の手
- 2:54:00~2:56:00 -- カメラの外でドラマが発生。ロビーがギャレットに13万5000ドルを返したことを別のプレイヤーが知る。私も同意見の別のプレイヤーがギャレットを「クソ野郎」と呼ぶ。
- 3:11:25~3:20:52 -- ロビーがギャレットに13万5000ドルを支払うことについてのテーブルでの議論
- 3:37:59から3:43:14まで - ロビーが手について解説
次の図の図形はすべて正方形です。青い正方形の辺の長さは不明です。三角形ABCの面積はいくらですか?
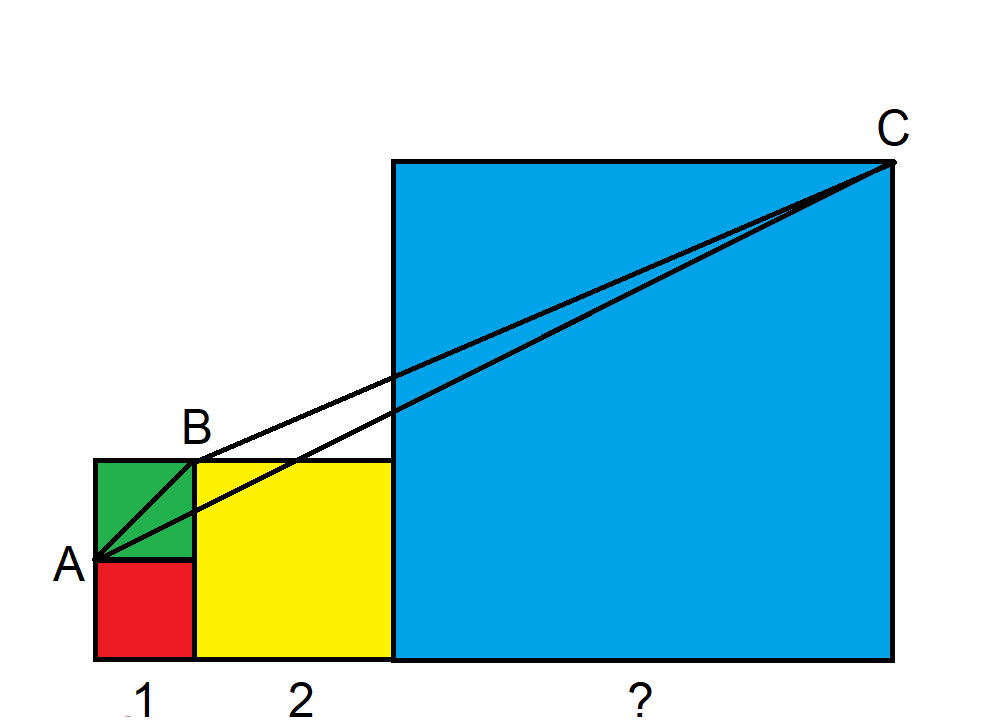
次の図を考えてみましょう。
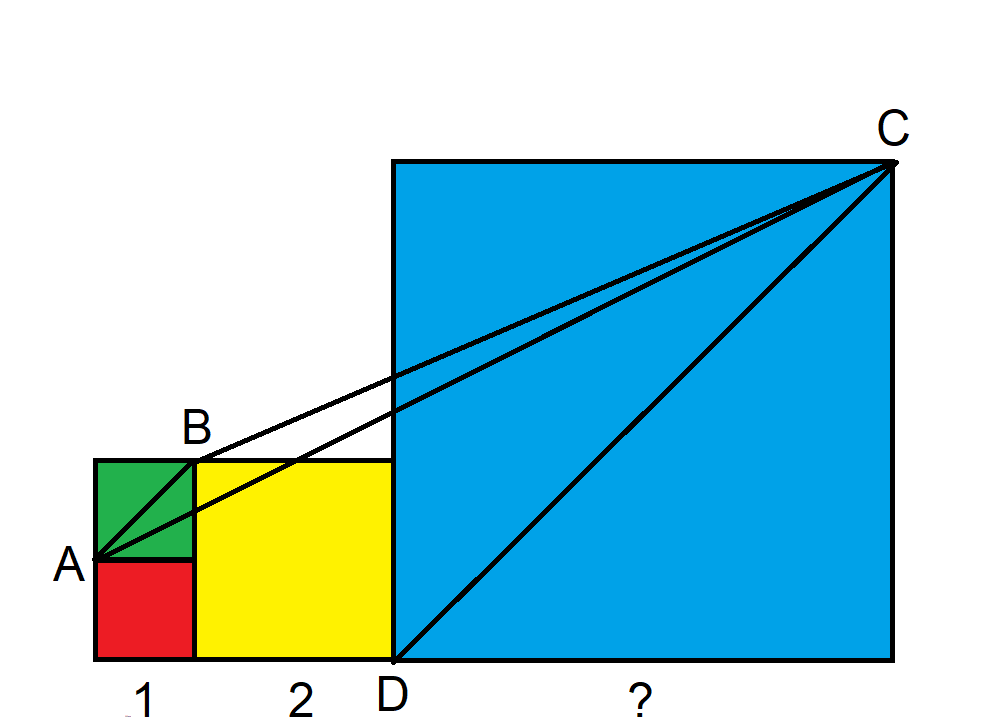
線分ABと線分CDはどちらも45度の角度をなしていることに注目してください。つまり、これらは平行です。
三角形の面積は(1/2)×底辺×高さであることを思い出してください。つまり、青い正方形の大きさは関係ありません。三角形ABCの高さは常に同じです。三角形Dの高さはどの三角形Cの高さも同じなので、面積は三角形ABDと同じです。
簡単な幾何学では、AB = sqrt(2) かつ BD = 2*sqrt(2) であることが分かります。したがって、ABC の面積は、ABD = (1/2) * sqrt(2) * (2*sqrt(2)) = 2 となります。


