Wizardに尋ねる #399
最初の画像から小さな正方形を取り除いてピースを並べ替えても、全体の面積は同じに見えます。どうしてそうなるのでしょうか?
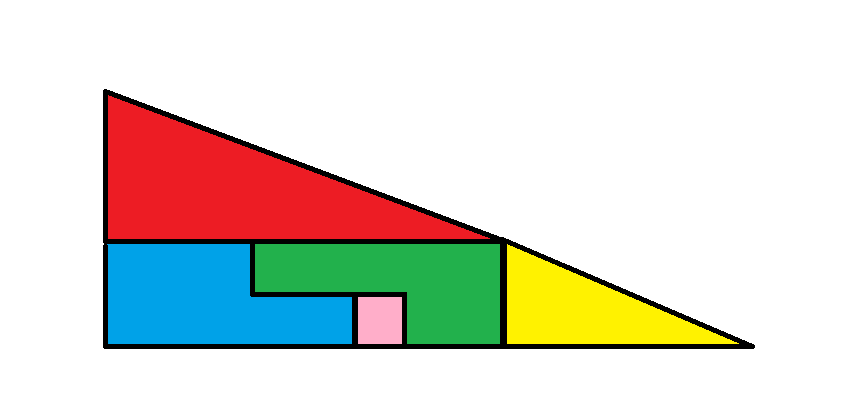
画像1
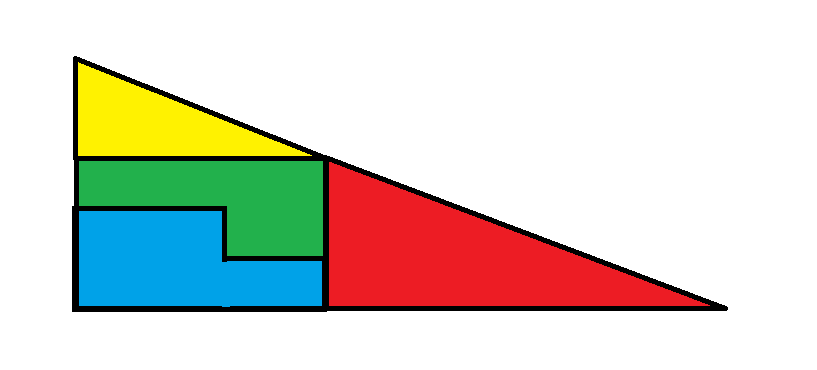
画像2
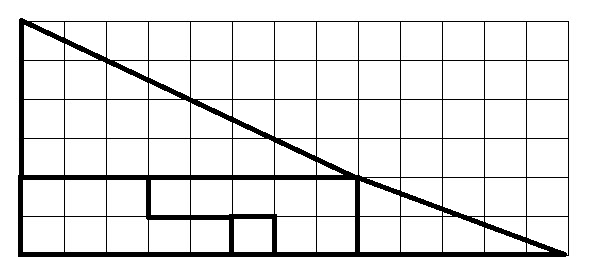
上の画像では、各ピースのサイズがよくわかるように、最初の画像をグリッド上に表示しています。
大きな赤い三角形の辺の長さが4と8であることに注目してください。次に、小さな黄色の三角形の辺の長さが2と5であることに注目してください。つまり、これらの三角形は比例していません。2つの三角形の斜辺の傾きは、どちらの図に描かれているのと同じではありません。一方の傾きは0.5で、もう一方の傾きは0.4です。どちらの図にも描かれているようにピースを配置すると、辺の長さが5と13の大きな三角形を形成しているように見えますが、実際には三角形ではありません。
赤い三角形の面積は 4*8/2 = 16 です。
黄色の三角形の面積は 2*5/2 = 5 です。
最初の画像では、他の 3 つのピースが 2 x 8 の長方形を形成し、合計面積は 16 になります。
2 番目の画像では、他の 2 つのピースが 3 x 5 の長方形を形成し、合計面積は 15 になります。
最初の画像の合計面積は、赤い三角形 + 黄色の三角形 + 大きな長方形 = 16 + 5 + 16 = 37 です。
2 番目の画像の合計面積は、赤い三角形 + 黄色の三角形 + 小さな長方形 = 16 + 5 + 15 = 36 です。
結論として、最初の画像の方が正方形が小さく、大きいです。どちらの場合も、ピースを全部合わせると大きな三角形になるように見えるのは錯覚です。実際はそうではありません。
広大な砂漠の端に16台のバイクが停まっています。各バイクはガソリン1タンクで100マイル(約160km)走行できます。すべてのバイクは満タンの状態でスタートします。バイク間でのガソリンの移し替えは許可されています。目標は、1台のバイクを出発地点からできるだけ遠くまで移動させることです。どこまで行けるでしょうか?
問題の鍵は、グループが少し距離を移動することです。そして、バイクの1台から残りのガソリンを取り出し、他のバイクのタンクに満タンにしましょう。
例えば、最初に満タンのガソリンを16等分し、各バイクに1台ずつ割り当てます。その後、全員が一緒に走行し、1/16タンク分消費すると、グループ全体の走行距離は100/16 = 6.25マイルになります。1台のバイクから1/16タンク分のガソリンを取り出し、残りの1/16タンク分を他の15台のバイクにそれぞれ供給すれば、ちょうど満タンになります。
同じ手順を繰り返しますが、残り15台のバイクで、燃料タンクの1/15で行ける距離、つまり100/15 = 6.666667マイルまで走行します。次に、1台のバイクからさらに1/15の燃料タンクを取り出し、残りの14台のバイクに燃料タンクの1/15をサイフォンで供給します。
このプロセスを続けると、最後のバイクの合計距離は (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338.072899 マイルになります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されました。
「眠れる森の美女のパラドックス」についてどう思いますか?
他の読者のために、「眠れる森の美女の問題/パラドックス」で問われている内容を以下に示します。
眠れる森の美女(SB)は実験に志願しました。実験の詳細は、以下のようにすべて彼女に正直に説明されました。
- 日曜日:SBは眠らされる。眠った後、公平なコインを投げる。
- 月曜日: SB は月曜日に起こされ、「コインが表になる確率はどれくらいですか?」と質問されます。答えた後、彼女は月曜日に起こったすべてのことを忘れる記憶喪失薬を投与されて再び眠らされます。
- 火曜日:コインが裏だったら、月曜日と同じことがまた起こります。表だったら、彼女は一日中寝ます。
- 水曜日: SB は再び起こされ、何も聞かれず、実験が終了したので家に帰ります。
問題は、月曜日、そしておそらく火曜日に尋ねられた質問に彼女がどのように答えるべきかということです。
私の答え
この実験を何百万回も繰り返すと、それぞれ同じ確率で次の 3 種類の目覚めが見られることが予想されます。
- コインが表に出ると、月曜日に目覚める。
- コインは裏が出ました。月曜日に目覚めました。
- コインは裏が出ました。火曜日に目覚めました。
これは、月曜日の起床回数がコイン投げの表と裏で均等に分散される必要があるためです。また、コインが裏になった場合、月曜日と火曜日の起床回数は完全に等しくなります。したがって、大規模なサンプルサイズでは、3つのグループすべてで起床回数はほぼ同じになります。
これらの覚醒のうち、3回に1回は表が出た後で発生します。つまり、コインが表になる確率は1/3です。
半分の陣営は、SB は目覚めるたびに追加の情報を与えられないため、コイントスの各結果が同等の可能性があると想定すべきだと主張します。
この問題に、コインが裏になった場合の覚醒回数を999,999回まで拡張します。表が出た後の覚醒は100万回に1回しか起こりません。つまり、どんな覚醒でも、裏が出た後の999,999回の覚醒のいずれかであると推測するのは容易です。言い換えれば、この場合の正解は1,000,000回に1回です。
さらに別の展開として、SBが毎回目覚めるたびにコイントスの結果を予測するよう求められたらどうなるでしょうか。もし彼女が正解すれば、1,000ドルを獲得できます。もし彼女が「表」と予測する戦略を持っていれば、(1/2)*1,000ドル=500ドルを獲得できると期待できます。もし彼女が「裏」と予測する戦略を持っていれば、(1/2)*2,000ドル=1,000ドルを獲得できると期待できます。つまり、SBが目覚めているという事実だけで、コインが裏になる可能性が高くなります。
私の説明が明確でなかったら、Wikipedia の「眠れる森の美女の問題」で、SB からの他の回答も含めて、私が説明するよりずっと詳しく説明されています。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されました。


