Wizardに尋ねる #405
x 2 - 3 = sqrt(x+3)。xについて解きます。
y = 両方の式とします。つまり、次のようになります。
- y = x^2 - 3
- y = 平方根(x+3)
どちらの式にも3があることに注意してください。両方の式を片方の辺に3を入れて表してみましょう。まず、次の式を得ます。
3 = x^2 - y
次に、上の 2 番目の方程式を二乗してみましょう。
y^2 = x+3
3 = y^2 - x
両方の式を 3 について等しくしてみましょう。
x^2 - y = y^2 - x
並べ替えてみましょう:
x^2 - y^2 + x - y = 0
(x+y)(xy) + x - y = 0
(xy)(x+y+1) = 0
まず xy = 0 を調べてみましょう:
xy = 0
y の代わりに y = x^2 - 3 を代入してみましょう。
x - (x^2 - 3) = 0
x^2 - x - 3 = 0
ピタゴラスの公式を使うと:
x = (1 +/- 平方根(1 + 12)/2
x = (1 + sqrt(13)/2 および x = (1 - sqrt(13)/2
次に、x+y+1 = 0 を調べてみましょう。
y の代わりに y = x^2 - 3 を代入してみましょう。
x + (x^2 - 3) + 1 = 0
x + x^2 - 3 + 1 = 0
x^2 + x - 2 = 0
ピタゴラスの公式を使うと:
x = (-1 +/- 平方根(1 + 8)/2
x = (-1 +/- 3)/2
x = 1、x = -2
したがって、私たちの答えは次の 4 つです。
- x = 1
- x = -2
- x = (1 + sqrt(13)/2 =~ 2.302776
- x = (1 - sqrt(13)/2 =~ -1.302776
この問題を解くための方法を提供してくれたSyberMathのYouTube動画「Solving x^2-3=sqrt(x+3)」に感謝します。この方法は6:28のところをご覧ください。
半径1の円の外側の点からは、円周の1/3が見えます。その点はどれくらい離れていますか?
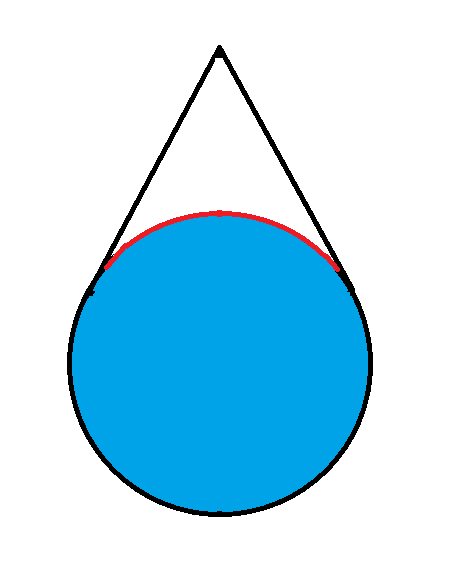
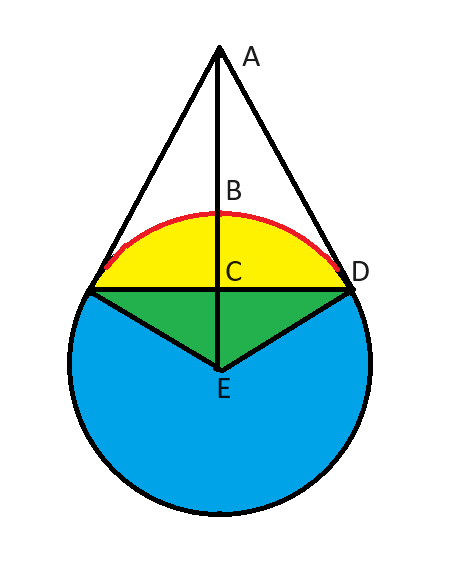
三角形ADEを考えてみましょう。次のことが分かっています。
- AD は円に接しているので、角度 ADE は 90 度です。
- 角度 AED は 60 度です。これは、E の緑色の三角形の角度が 120 度 (全体の 360 度の 1/3) であるためです。
- 角度 EAD は三角形 ADE のもう 30 度でなければなりません。
これは典型的な30-60-90三角形です。この三角形の辺は1、2、そして平方根(3)に比例することは誰もが知っているはずです。
この場合、質問にあるように ED = 1 です。AE はその距離の 2 倍、つまり 2 です。
2は点から円の中心までの距離です。点から円上の最も近い点までの距離を求められます。そこで半径を引きます。つまり、答えは2-1 = 1です。
ボブとトムは鉄橋を渡っていて、スタート地点から3分の1の地点まで来ています。その時、後ろから列車が近づいてくる音が聞こえました。二人とも時速5マイル(約8キロメートル)で走ることができます。ボブは振り返り、トムは前へ走ります。二人とも1秒未満の差で列車に遭遇しました。列車の速度はどれくらいでしたか?
距離 = 速度 * 時間 を覚えておいてください。これは d = r*t と表されます。
これを書き直すと、t = d/r となります。
橋の始まりでボブと列車が出会う時間はどちらも同じです。
では、次のようにしましょう。
- x = 列車の最初の位置と橋の始まりの間の距離。
- r = 列車の速度
まず、走って戻るボブを見てみましょう。ボブと列車が橋の始点で出会うように、t を表現しましょう。
ボブ: t = (1/3)/5
列車: t = x/r
t の 2 つの式を等しくすると、次のようになります。
(1/3)/5 = x/rr/3 = 5倍
r = 15倍
次に、先頭を走るトムを見てみましょう。トムと列車が橋の始点で出会うように、t と表してみましょう。
トム: t = (2/3)/5
列車: t = (1+x)/r
t の 2 つの式を等しくすると、次のようになります。
(2/3)/5 = (1+x)/r
2r/3 = 5(1+x)
2r = 15(1+x)
2r = 15 + 15x
この時点では次のようになります。
- r = 15倍
- 2r = 15 + 15x
最初の式の r の表現を 2 番目の式に代入してみましょう。
30倍 = 15 + 15倍
15x = 15
x = 1
r = 15x を思い出してください。
したがって、列車の速度は 15 * 1 = 15 mph となります。


