Wizardに尋ねる #410
「ザ・プライス・イズ・ライト」の「Ask the Wizard」コラム#115で、Plinkoゲームについて質問されましたね。しかし、特別番組では賞金が変更になることもあるようです。例えば、「ビッグ・マネー・ウィーク」では、賞金は左から順に500ドル、1000ドル、2500ドル、0ドル、200000ドル、0ドル、2500ドル、1000ドル、500ドルでした。パックが落とされる各位置の期待値はどれくらいでしょうか?また、開始位置が与えられた場合、パックが特定の賞品に落ちる確率はどれくらいでしょうか?
パックを落とすスタート位置は9つあります。ただし、賞品とペグの配置は左右対称なので、ここでは5つだけに注目します。左端から1から5まで、それぞれにラベルを付けましょう。
終了位置も 9 つあります。左から最初の 5 つに 1 から 5 のラベルを付けましょう。

次の表は、落下した位置 (上の行) に応じて、特定のスポット (左の列) に着地する確率を示しています。
| 着陸地点 | 1または9をドロップ | 2または8をドロップ | ドロップ3または7 | 4または6をドロップ | ドロップ5 |
|---|---|---|---|---|---|
| 1または9 | 0.225586 | 0.193359 | 0.121094 | 0.056641 | 0.032227 |
| 2または8 | 0.386719 | 0.346680 | 0.250000 | 0.153320 | 0.113281 |
| 3または7 | 0.242188 | 0.250000 | 0.257813 | 0.250000 | 0.242188 |
| 4または6 | 0.113281 | 0.153320 | 0.250000 | 0.346680 | 0.386719 |
| 5 | 0.032227 | 0.056641 | 0.121094 | 0.193359 | 0.225586 |
| 合計 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
次の表は、ご質問のビッグマネーウィークにおける各ドロップポジションの期待値を示しています。予想通り、プレイヤーはパックを最大賞金の方向にドロップするはずです。
| ドロップ場所 | 予想される勝利 |
|---|---|
| 1または9 | 7,550.29ドル |
| 2または8 | 12,396.48ドル |
| 3または7 | 25,173.83ドル |
| 4または6 | 39,478.52ドル |
| 5 | 45,852.05ドル |
ガブリエルの角のパラドックスとは何ですか?
まず、xの値が1から無限大までの場合のy=1/xの式から得られる曲線を考えてみましょう。xの値が17までの場合、グラフは次のようになります。
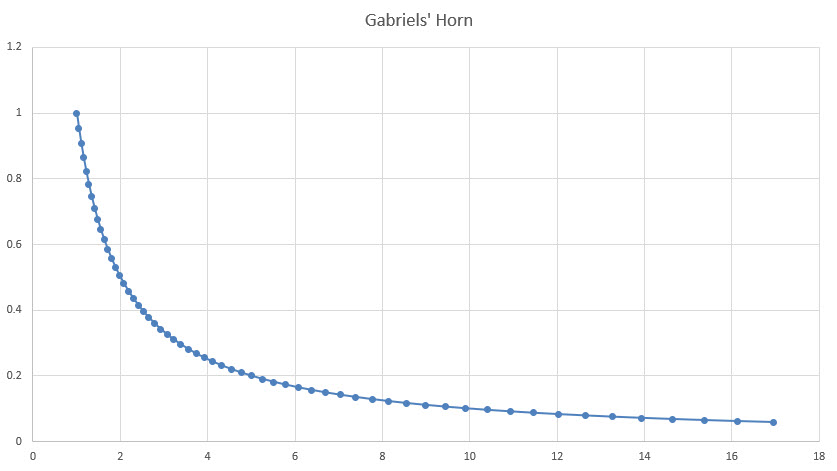
次に、その曲線をx軸を中心に回転させてみましょう。すると、先端が無限に長い角のような形になります。数学者はこれを「ガブリエルの角」と呼ぶのでしょうか?

画像出典: Soul of Mathematics .
次に、ガブリエルの角笛に関する質問について考えてみましょう。
- 音量はどのくらいですか?
- 表面積はどれくらいですか?
答えは次のとおりです。
- 体積 = π = 円周率。
- 表面積 = 無限大
これらの答えを示した私の作品は、こちら(PDF) でご覧いただけます。
このパラドックスの本質は、体積は有限なのに表面積は無限であるのはなぜか、という点です。
認識されているパラドックスは、2次元と3次元を混同したときに発生します。しかし、そうしてはいけません。半径1の円Aと半径1.1の円Bを考えてみましょう。円Aは円Bの内側にあります。
円Aの円周は2π =~= 6.283185、円Bの面積は1.1^2π =~ 3.801327です。円Bは円Aよりも大きいですが、面積は円Bの円周よりも小さいことに注意してください。これは、円Bの円周が円Aの面積の一部であるという意味ではありません。面積と円周は異なる次元における異なる測定値であり、比較すべきではありません。
別の見方をすると、無限の数の溝がある円 A からレコードを作った場合、それらの溝の長さは無限になります。
ガブリエルの角笛に戻って、半径 1、1/2、1/3、1/4 などの円の個別のケースに単純化することを検討してください...
これらの円の体積の合計はπ*(1/1 + 1/4 + 1/9 + 1/16 + ...)となります。よく知られている無限級数があります。
1/1 + 1/4 + 1/9 + 1/16 + ... = π^2/6 =~ 1.644934。
もう1つの円周率の項を追加すると、円の面積の合計は pi^3/6 =~ 5.167713 になります。
一方、円周の合計は 2*pi(1/1 + 1/2 + 1/3 + 1/4 + ...) です。
これは数学でよく知られているもう 1 つの無限級数であり、「調和級数」と呼ばれます。
1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = 無限大。
2*pi*∞は依然として∞に等しい。
この論理を円間の無限に小さい距離に拡張すると、ガブリエルの角笛が得られます。
ネイサンは100ポンドの豆を買いました。豆の重量の99%は水分です。彼女は豆を日光に当てて乾燥させました。翌日、豆の98%が水分であることがわかりました。重さはどれくらいでしょうか?
させて:
- w = 元の水の重量。
- w' = 豆を乾燥させた後の水分の重量。
- x = 豆に含まれるその他のすべての重量。
最初の日に与えられるもの:
w + x = 100
w/(w+x) = 0.99
最初の方程式を 2 番目の方程式に代入します。
100倍 = 0.99
w = 99
したがって、x=1 です。
翌日、私たちは次のことを与えられました。
w'/(w'+x) = 0.98
w' = 0.98*(w'+x)
0.02w' = 0.98x
x=1 であることがわかっているので、
0.02w' = 0.98
w' = 0.98/0.02 = 49
翌日の合計重量は x+w' = 1+49 = 50 です。


