Wizardに尋ねる #413
次の要件を満たすシークレットサンタのギフト交換を行う方法はありますか?
- 誰も自分自身に贈り物をしません。
- やり直しはできません。
- 誰のために買うのかということ以外、誰も何も知りません。
- どの試合も可能性は同じです。
はい！私は以下をハンナ・フライ法と呼んでいます。
- 下図のようにカードのセットを作成します。各カードの上部と下部にそれぞれ異なる番号を付けます。以下の例では、番号は23です。
- カードをシャッフルして重ね直します。
- スタックをそのままにして、各カードを中央のラインに沿ってカットし、2 つのスタックを作成します。
- スタックの 1 つを切り取って、カットを完了します。
- 各山の一番上のカードを、一度に 1 枚ずつ各参加者に配布します。
- 番号付きリストを作成し、全員に番号を書いてもらいます。
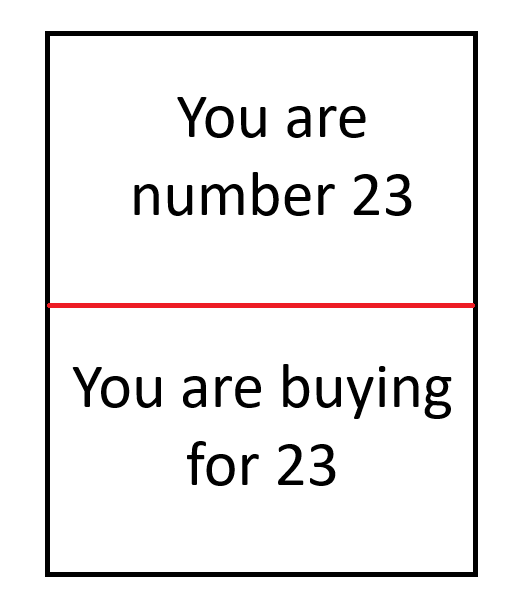
この手順を踏むと、参加者全員が2枚のカードを持ちます。カードには、例えば「あなたは13番です」と「あなたは7番の人のために買います」と書かれています。リストが記入されると、参加者は誰に何を買うべきかは分かりますが、誰が自分のために買うのかは分かりません。
プールは塩水で満たされています。プールの水量は1000立方メートルです。庭のホースから毎時1立方メートルの速度で真水がプールに流れ込みます。真水がプールに流れ込むと同時に、反対側からも同じ速度で水が流れ出ます。プールの塩水濃度が1%になるまでにはどれくらいの時間がかかりますか？
答えは2000 ln(10) =~ 4605.170186 時間 =~ 191.8821 日です。
これが私の解決策です（PDF）。
平均すると、各プラトン立体において、以前に振った面をもう一度振るには何回必要ですか?
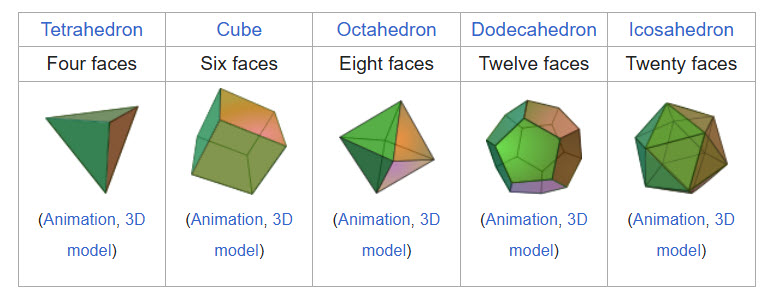
画像出典： Wikipedia
辺の数による答えは次のとおりです。
| サイド | 平均ロール |
|---|---|
| 4 | 3.218750 |
| 6 | 3.774691 |
| 8 | 3.846558 |
| 12 | 5.036074 |
| 20 | 6.293585 |
6 面立方体の場合を考えてみましょう。
- 実験が2回ロールで終了する確率は1/6です。
- 実験が3回ロールで終了する確率は (5/6)*(2/6) です。
- 実験が4回ロールで終了する確率は (5/6)*(4/6)*(3/6) です。
- 実験が5回で終わる確率は、(5/6)*(4/6)*(3/6)*(4/6)です。
- 実験が 6 回で終了する確率は (5/6)*(4/6)*(3/6)*(2/6)*(5/6) です。
- 実験が 7 回で終了する確率は、(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) です。
pr(n) = 確率実験が n 回のロールで終了するとします。
期待されるロールは、2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =
2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3.774691358。