Wizardに尋ねる #419
シーケンシャルロイヤルで配当を高くできるビデオポーカーの戦略をご存知ないようです。教えていただけますか?
まず、ビデオポーカーの用語をいくつか説明しておきます。
- シーケンシャルロイヤル = ローからハイのみ (10-JQKA)
- リバーシブルロイヤル = 両方向 (10-JQKA または AKQJ-10)
さらに混乱を招くのは、この用語を誰もが使っているわけではないことです。また、シーケンシャルロイヤルに別項目があるゲームでは、両方向に支払われる可能性があるということです。ルール画面でこの点が明確になれば幸いです。
とはいえ、シーケンシャルロイヤルやリバーシブルロイヤルの可能性があるハンドをプレイする簡単で完璧な方法は、私のビデオポーカー計算機に入力することです。リンクはこちらです:
私のサイトをマシンで使用できない、または使用したくない場合は、リバーシブル ロイヤルが 5 クレジットの賭けに対して、すでに配置されているカードの枚数に応じて 50,000 を支払う場合のロイヤルの平均勝利額がここに記載されていますので注意してください。
- リバーシブルロイヤル4個 = 10,000
- リバーシブルロイヤル3個 = 5,400
- リバーシブルロイヤル2 = 2,333
- リバーシブルロイヤル(中央位置)に1 = 1,567
- リバーシブルロイヤル(中央位置ではない)に1 = 1,183
- 0からリバーシブルロイヤル = 800
シーケンシャル ロイヤル ゲーム (低額から高額のみの支払い) の場合は、位置に関係なく 1,183 という数字を使用します。
これらの数字を使って、私のビデオポーカー戦略メーカーを使って、ロイヤルの平均勝利数ごとに個別の戦略を作成します。そして、ロイヤルのカードが正しい位置にある枚数に応じて、マシンでその戦略を適用します。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
ケロッグは、アップルジャック、フロステッドフレーク、クレイブの球形バージョンを新たに発売しました。球形にすることで、より濃厚なグレーズが作れると主張しています。実際、「計算してみました」と書かれていますが、本当に計算通りなのでしょうか?

いや!!!!!!!!! いや、計算が間違ってるんです。実際、表面積と体積の比率を最大化したいなら、球体は最悪の三次元形状なんです。
まず、箱の裏側にある表面積の式を見てみましょう。

彼らは、球体(おそらくドーナツの穴と呼ぶもの)の表面積は 4πr 2 (r = 半径)であると正しく述べています。
しかし、トーラス(おそらくドーナツと呼ぶべきもの)の表面積が2π 2 rRと誤って記載されています。正しい式はその2倍、つまり4π 2 rRです。rとRについては次の図を参照してください。
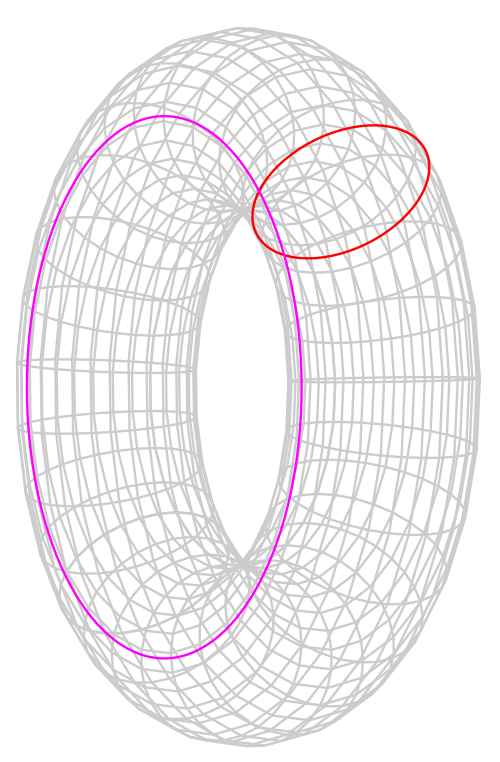
r = 赤い円の半径
R = トーラスの最も近い部分から中心までの距離。
画像ソース:トーラスに関する Wikipedia ページ。
球体の代わりに、ドーナツにフロスティングを塗るように、トーラスの半分だけに釉薬を塗るという方法もあるかもしれません。しかし、トーラス型の伝統的なアップルジャックをよく見ると、全体に釉薬が塗られていることがわかります。
次に、球とトーラスの両方の体積の公式も示したいと思います。
- 球面 = (4/3)πr 3
- トーラス = 2π 2 r 2 R
念のため、表面積の計算式は体積の導関数です。
r=1、R=1のトーラスの場合、表面積は39.478418、体積は19.739209となります。興味深いことに、表面積と体積の比、つまり釉薬比はちょうど2です。
体積を等しくするには、球の半径を1.676539とする必要があります。この球の半径では、表面積は35.321350、体積は19.739209となります。表面積と体積の比、つまり釉薬比は1.789400です。
言い換えれば、トーラスは同じ体積に対してより大きな表面積または釉薬を提供します。
先ほど、球は体積に対する表面積の比を最大化することが目的なので、3次元形状として選ぶには最悪の形状だと述べました。これは等周不等式として知られています。これは証明されていますが、自明のことだと思います。例えば、泡は表面積を最小化し、強度を最大化しようとし、球形をしています。
結論として、アップルジャックスなどの球形またはドーナツ型のものを買うべきです。グレーズの量を増やすのではなく、最小限に抑えたいのであれば、そうすべきです。私にとってはそれが目標です。なぜなら、このシリアルは甘すぎると感じるので、グレーズの量を減らしてほしいからです。また、ケロッグは虚偽広告で、珍しく魔法使いから非難を浴びています。
この質問は私のWizard of Vegas フォーラムで尋ねられ、議論されています。
詳細については、MindYourDecisions チャンネルの Presh Talwalkar による YouTube ビデオ「 Internet spots big mistakes on Kellogg's cereal box 」(私のお気に入りの 1 つです!) をお勧めします。
ビデオポーカーで配られた勝ちのハンドの確率はどれくらいですか?
この質問に対する答えは、プレイヤーがディールで勝ち手を引いた場合にボーナス機能を提供するビデオポーカーのいくつかのバリエーションで実際に応用できることがわかります。
答えはビデオポーカーの形式によって異なります。以下の表は、ワイルドカードなしの52枚のデッキでビデオポーカーをプレイした場合、最低配当のジャックのペアから始まり、すべての可能なイベントの組み合わせの数と確率を示しています。
| 手 | 組み合わせ | 確率 |
|---|---|---|
| ロイヤルフラッシュ | 4 | 0.000002 |
| ストレートフラッシュ | 36 | 0.000014 |
| フォー・オブ・ア・カインド | 624 | 0.000240 |
| フルハウス | 3,744 | 0.001441 |
| フラッシュ | 5,108 | 0.001965 |
| 真っ直ぐ | 10,200 | 0.003925 |
| スリーオブアカインド | 54,912 | 0.021128 |
| 2組 | 123,552 | 0.047539 |
| ジャック以上 | 337,920 | 0.130021 |
| その他すべて | 2,062,860 | 0.793725 |
| 合計 | 2,598,960 | 1.000000 |
ジャックまたはベターのビデオ ポーカー ゲームで勝つ確率は 0.206275 です。
2 番目の表は、52 枚のカード デッキで 2 がワイルドであるビデオ ポーカーで、最低配当のスリー オブ ア カインドから始まり、ディールで発生する可能性のあるすべてのイベントの組み合わせの数と確率を示しています。
| 手 | 組み合わせ | 確率 |
|---|---|---|
| ナチュラルロイヤルフラッシュ | 4 | 0.000002 |
| 4つのデュース | 48 | 0.000018 |
| ワイルドロイヤルフラッシュ | 480 | 0.000185 |
| ファイブ・オブ・ア・カインド | 624 | 0.000240 |
| ストレートフラッシュ | 2,068 | 0.000796 |
| フォー・オブ・ア・カインド | 31,552 | 0.012140 |
| フルハウス | 12,672 | 0.004876 |
| フラッシュ | 14,472 | 0.005568 |
| 真っ直ぐ | 62,232 | 0.023945 |
| スリーオブアカインド | 355,080 | 0.136624 |
| その他すべて | 2,119,728 | 0.815606 |
| 合計 | 2,598,960 | 1.000000 |
デュース ワイルド ビデオ ポーカー ゲームで勝つ確率は 0.184394 です。
3 番目の表は、ジョーカーを含む 53 枚のカードのデッキを使用したビデオ ポーカーで、キングのペアの最低配当ハンドから始まり、配布されるすべての可能なイベントの組み合わせの数と確率を示しています。
| 手 | 組み合わせ | 確率 |
|---|---|---|
| 5枚組 | 13 | 0.000005 |
| ロイヤルフラッシュ | 24 | 0.000008 |
| ストレートフラッシュ | 180 | 0.000063 |
| フォー・オブ・ア・カインド | 3,120 | 0.001087 |
| フルハウス | 6,552 | 0.002283 |
| フラッシュ | 7,804 | 0.002719 |
| 真っ直ぐ | 20,532 | 0.007155 |
| 3つ揃い | 137,280 | 0.047838 |
| 2組 | 123,552 | 0.043054 |
| キング以上 | 262,956 | 0.091632 |
| その他すべて | 2,307,672 | 0.804155 |
| 合計 | 2,869,685 | 1.000000 |
ジョーカー ポーカー (キング以上) ビデオ ポーカー ゲームで勝つハンドの確率は 0.195845 です。


