Wizardに尋ねる #426
シリアル番号が1から順に番号付けされているとします。流通している最大数は不明です。n個の番号をランダムに抽出した場合、最大のシリアル番号の最良の推定値はいくらでしょうか?
答えを求める方法として、私はシリアル番号間の平均間隔を求めるのが好きです。これは、最大値をサンプルサイズで割ることで計算します。例えば、サンプル内の最大のアイテムが1,000で、サンプルサイズが5の場合、平均間隔は1000/5=200となります。次に、その間隔を最大値に加算することで、推定最大値を算出します。この例では、1000+200=1200となります。
同じ数値を得るための一般的な公式はM*(k+1)/kです。ここで、Mは最大値、kは観測数です。この例では、1000*(6/5) = 1200となります。
ABCD は、辺の長さが 10 の正方形です。次の図に示すように、その内側には半円と四分の一円が内接しています。
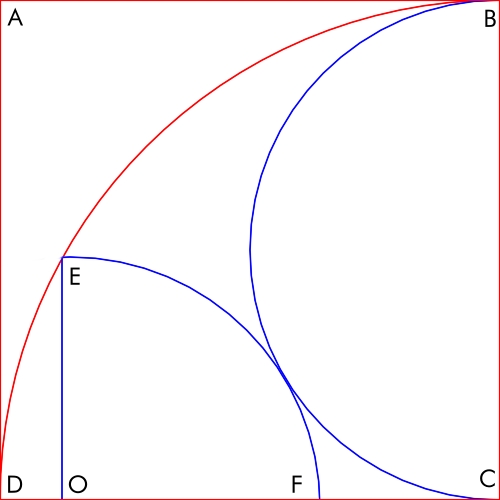
OEの長さはどれくらいですか?
次の図を考えてみましょう。
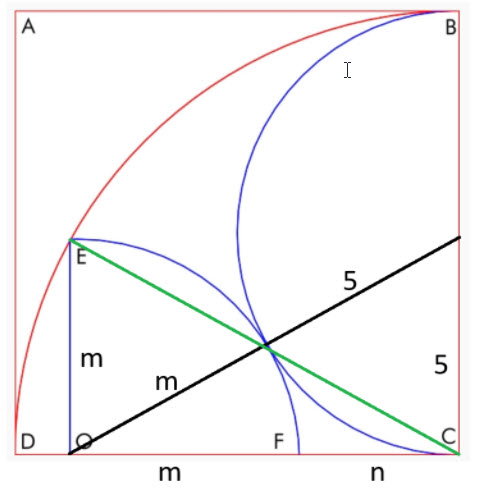
ここに2つの直角三角形があります。1つは斜辺が緑、もう1つは斜辺が黒です。2つのピタゴラスの定理を立ててみましょう。
- 緑の斜辺: m 2 + (m+n) 2 = 10 2
- 黒い斜辺: 5 2 + (m+n) 2 = (m+5) 2
最初の式を(m+n) 2 = 10 2 - m 2と変形してみましょう。
その値を (m+n) 2 の2 番目の式に代入してみましょう。
5 2 + 10 2 - m 2 = (m+5) 2
25 + 100 - m 2 = m 2 + 10m + 25
2m 2 + 10m - 100 = 0
m 2 + 5m - 50 = 0
ピタゴラスの公式を使用して m を解きます。
m = (-5 +/- 平方根(25 + 200))/2
m = 5 または -10。5 が唯一の合理的な答えです。
この質問は、 Wizard of Vegas の私のフォーラムで尋ねられ、議論されています。
多数の学生が10問のテストを受けています。すべての設問は正誤です。2つのテストの答えが少なくとも2問異なる場合、最大何人の学生がテストを受けることができますか?
1 つのテストをキー テストと呼ぶことにします。
グループ 1 = キー テストと正確に 2 つの質問が異なる他のテストの数は、combin(10,2) = 45 です。
キー テストから 3 だけ異なる方法の数を計算するつもりはありません。その理由は、それらの方法のいくつかは、10 個中 9 個がグループ 1 のテストに一致するためです。
グループ2 = 他のテストがキーテストからちょうど4問だけ異なる場合、その数はcombin(10,4)=210です。これらのテストはいずれも、グループ1のどのテストとも少なくとも2問は異なります。
この論理を繰り返すと...
- グループ 3 = キー テストと正確に 6 つの質問が異なる他のテストの数は、combin(10,6) = 210 です。
- グループ 4 = キー テストと正確に 8 つの質問が異なる他のテストの数は、combin(10,8) = 45 です。
- グループ 5 = キー テストと正確に 10 個の質問が異なる他のテストの数は、combin(10,10) = 1 です。
したがって、答えは、グループ 1 から 5 の合計にキー テストの 1 を加えた値 = 1+45+210+210+45+1 = 512 となります。
その数字は2^9と同じです。偶然でしょうか?いいえ!
大きなグループから奇数個のアイテムを取り出す方法の数は、偶数個を取り出す方法の数と同じです。これは、大きなグループ内のすべてのアイテムが、選ばれるか選ばれないかのどちらかになるからです。n個のアイテムからなるグループでは、各メンバーが選ばれるか選ばれないかの組み合わせは2のn乗通りあります。もしこれらを2進法で体系的に並べると、選ばれる組み合わせの数は偶数と奇数が交互に現れます。グループ全体の数は2のn乗で、それ自体は偶数なので、2のn乗の半分は偶数になります。
したがって、グループ1から5の合計は、キーテストに一致する質問を偶数個選ぶ方法の数です。これは、キーテストに一致する質問を奇数個選ぶ方法の数と等しくなります。キーテストに一致する、または一致しない方法の総数は2^10 = 1024です。そのうち半分は偶数回一致します。したがって、答えは1024/2 = 512です。
この質問は、 Wizard of Vegas の私のフォーラムで尋ねられ、議論されています。


