Wizardに尋ねる #427
ケーキは次のように分割されます。
- 最初の人は1%を得る
- 2人目は残りの2%を受け取る
- 3人目は残りの3%を受け取る
- 等々。
一番多くのケーキをゲットできるのは誰でしょう?スプレッドシートや力ずくの計算は禁止です。
これが私の解決策です(PDF)。
この質問は、 Wizard of Vegas の私のフォーラムで尋ねられ、議論されています。
この数学パズルは、 Mind Your Decisions YouTube チャンネルのおかげで作成できました。
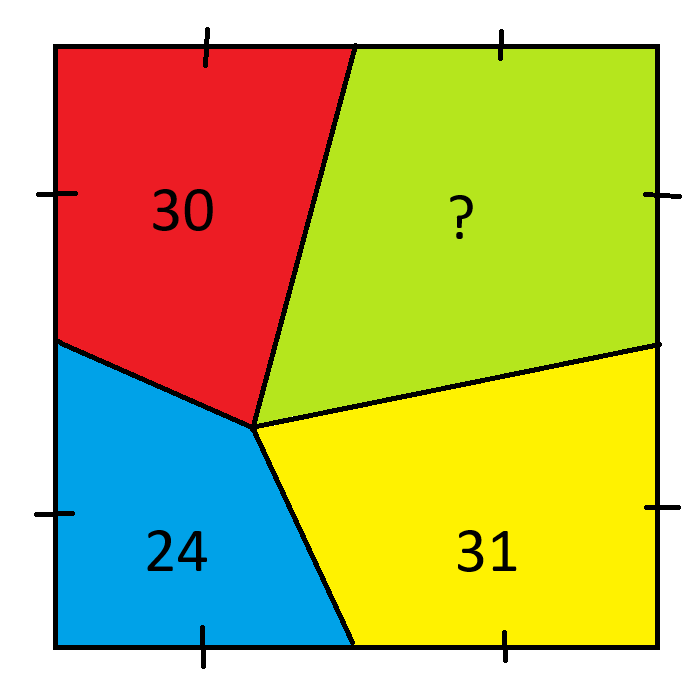
緑色の領域の面積はどれくらいですか?
まず、4つのピースの交点から各角まで4本の線を引きます。次に、8つのピースに次のようにラベルを付けます。
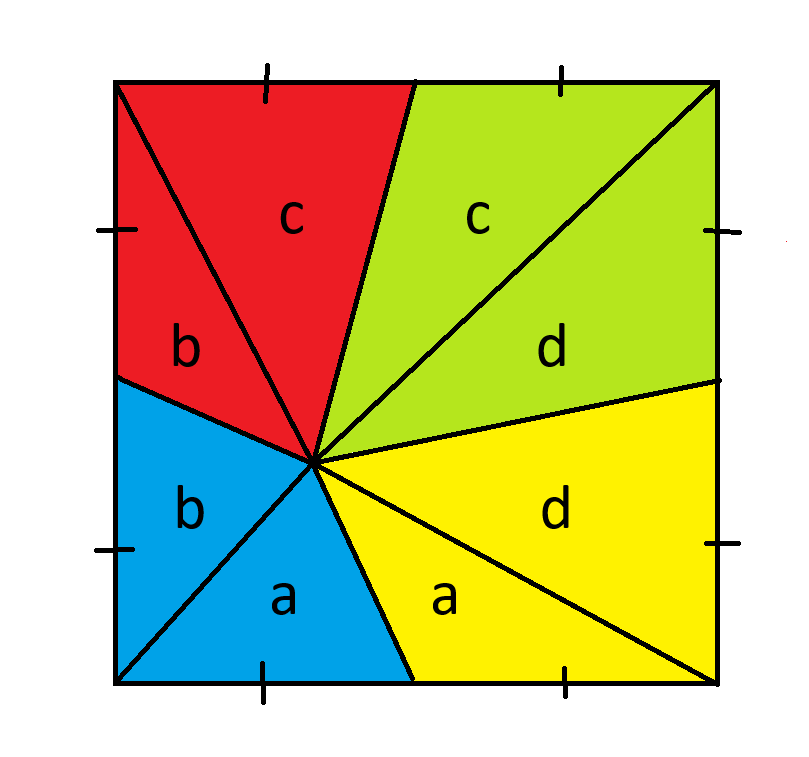
三角形の面積は底辺×高さ/2であることを思い出してください。すべての三角形の底辺は同じなので、高さが等しい三角形は面積が同じであるとみなすことができます。
この時点でわかっていること:
- (1)A+B = 34
- (2)B+C = 42
- (3)A+D = 30
式(2)と式(3)を加えると、
A+B+C+D = 72
そこから式(1)を引き算してみましょう。
C+D = 38、これが答えです。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されました。
このパズルの元となったのは、「98% の人がこの数学の問題を解けなかった」というタイトルのYouTube 動画です。
複数の値の平均を求めたいとします。オリンピックの体操競技の採点のように、最高値と最低値を除外するのはどうでしょうか?特定の地域の1平方フィートあたりの平均値を求めるのが目的だとしましょう。
いい質問ですね。あなたがおっしゃっているのは、トリム平均と呼ばれるものです。トリム平均と真の平均値の分散を表す統計量は知りません。他に良いアイデアがなかったので、自分で実験してみました。
ご質問にお答えするために、10組の値から10万個のサンプルを採取しました。各値は標準正規分布、つまり平均0、分散1に従って分布していました。そして、10個の値全体の平均と、切り取られた8個の値の平均を調べました。
10個の値すべてをサンプリングした場合の標本平均値と真平均値の平均差は0.003450でした。同じ方法でトリム平均値の平均を取った場合の平均差は0.003445でした。私の意見では、これはどちらの手法が優れているかを断言するには十分な有意差ではありません。また、私の実験に適した方法が、別の用途では必ずしも適切とは限りません。
結論として、私は頻繁にこう言うわけではありませんが、明確な数学的答えを持っていません。
正方形または三角形の底面を持つ球体を積み重ねる、より効率的な(つまり、無駄なスペースが最も少ない)方法は何ですか?


これに対する私の答えは、球の数が無限大に近づくにつれて、球の体積とそれを囲むピラミッドの体積の比率が最大になるピラミッドはどれかということでした。
これが私の解決策です(PDF)。
後で気づいたのですが、この質問はAsk the Wizard #350でも聞かれていました。しかし、この解決策の方が良いと思います。


