ブラックジャック - 基本戦略(特定の手)
ウィズ、君は最高だ!ネット上でダントツのギャンブルサイトを運営しているね。私もアクチュアリー(ACAS)なので、数学のスキルをうまく活用している人を見るのは大好きです。
質問です。レイトサレンダーが認められている場合、10が出ている時に8をスプリットしますか? おそらくそうだと思いますが、ブラックジャックで最も難しいプレーの一つは、8と10をスプリットすることです。
余談ですが、つい最近3日間ラスベガスに滞在しました。まだラスベガスに行っていない方は、ぜひラスベガスクラブと世界で最もリベラルなブラックジャックのルールを試してみてください。3枚または4枚のカードでダブルダウンが可能、6枚で21以下の場合は自動的に勝ち、レイトサレンダーも可能です。6デッキの場合、ハウスアドバンテージは0.14%と計算しました。お疲れ様でした!
ジムさん、親切なお言葉ありがとうございます。はい、レイトサレンダーが提案されたとしても、8をスプリットするべきです。スプリット後にダブルができない場合でも、サレンダーは拒否すべきです。スプリット後にダブルができない2デッキゲームの場合、10に対して8をスプリットした場合の期待値は-0.480673で、サレンダーした場合の-0.5よりも優れています。
「世界で最も自由なブラックジャックルール」という彼らの主張とは裏腹に、通りの向かいにあるホースシューやゴールデンゲートには、もっと良いシングルデッキゲームがあります。ラスベガスクラブの6デッキは、プレイヤーにとって不利に働きます。彼らの看板に騙されても気にしないでください。私自身、ルールの違いがもたらす影響を知る前の若い頃に、騙されたことがあります。
追記:この質問の後、ラスベガスクラブは「世界で最もリベラルなブラックジャックルール」と呼ばれるルールを改正し、ブラックジャックの配当を6対5に引き上げました。6対5では、ブラックジャックとして認められるゲームとは言えません。他の場所で簡単に見つけられる、普通の3対2のゲームの方がずっと有利です。
シングルデッキのブラックジャックでは、カードは裏向きで配られるのですか? また、シングルデッキの一般的なルールは何ですか? ダブルダウンは9-11または10-11の場合のみとおっしゃっていましたが、スプリット後のダブルダウン、ディーラーがソフト17をヒットした場合など、シングルデッキの一般的なルールをご存知ですか? 私はベーシックストラテジーのプレイヤーで、シングルデッキのルールがどのようなものなのかを知りたいです(6デッキか8デッキしかプレイしたことがありません)。blackjackinfo.comから完璧なスプレッドシートを作成したいので、ご協力ありがとうございます。
シングルデッキのブラックジャックのルールは通常厳格です。カードは裏向きで配られます。ダブルダウンは通常、9対11、または10対11に制限されています。ディーラーはソフト17をヒットし、スプリット後のダブルダウンはおそらく認められません。ブラックジャックの配当が3対2未満の場合は、シングルデッキのゲームでは一般的にそうなりますので、絶対にプレイしないでください。
私のサイト「Wizard of Vegas 」では、ラスベガスの比較的最新のブラックジャックのルールをいつでもご覧いただけます。
ブラックジャックの戦略では、A、10、9に対して16でサレンダーすると書かれています。これらのカードに対しては8のペアをスプリットするべきだとおっしゃっていますが、8のペアは16なのでサレンダーすべきだと聞いたことがあります。どう思われますか?
8 を 2 枚降伏するように言った人は誰であれ、アメリカのレイトサレンダーを前提とした間違ったアドバイスをしました。8 を 10 に対してスプリットする理由を説明するために、私のブラックジャックの付録 9b を確認してください。これは、任意の初期状況における任意のプレイの期待収益を示しています。この表は、スプリット後にダブルが可能な場合、ダブルデッキで 8 を 10 に対してスプリットすると、期待収益が -0.4706 になることを示しています。言い換えれば、平均して初期ベットの 47.06% を失うことが予想されます。これは、降伏した場合に失う 50% よりも少ないです。スプリット後にダブルが不可能な場合、収益率は -0.4801 で、これも -0.5 を超えます。8 を 9 またはエースに対してスプリットすると、さらに大きな収益が得られます。
ディーラーがホールカードをチェックし、ブラックジャックを持っていないのなら、なぜエースに対してソフト18をヒットするのでしょうか? また、11でダブルしないのはなぜでしょうか?
ブラックジャックでは、単純な答えはめったにありません。起こりうるすべてのことを考慮し、すべての結果をその確率で秤にかける必要があります。最善のプレイとは、期待リターンが最大のプレイです。私のブラックジャック付録 9bによると、ダブルデッキのゲームでエースに対してソフト 18 をヒットした場合の期待リターンは -0.1004 で、スタンドした場合の期待リターンは -0.1005 です。つまり、ヒットする方がほんの少しだけ良いということです。エースに対して 11 を出すのも、非常にギリギリのプレイです。これは実際にはシングルデッキでもダブルデッキでも構成に依存します。言い換えれば、合計 11 になる 2 枚のカードによって、ハンドのプレイ方法が決まります。ただし、構成に依存する基本戦略の例外を記憶したくない場合は、シングルデッキでもダブルデッキでもエースに対して 11 でダブルし、4 つ以上のデッキでヒットするべきです。
こんにちは、サイトをとても気に入っています!ブラックジャックでディーラーがエースを出している場合、イーブンマネーを取るか、そのままプレイを続けるかの選択肢があります。イーブンマネーを取るべきか、それともプレイを続けるべきか?
これは、保険をかけるという決断を別の角度から見ています。イーブンマネーを取った場合の期待収益は、明らかに 1.0 ユニットの賭けです。簡単にするために、カードのデッキが無限にあると仮定しましょう。ディーラーがブラックジャックを持っている確率は 4/13 で、そうでない場合は 9/13 です。ディーラーがブラックジャックを出した場合はプッシュします。そうでない場合は 1.5 ユニット勝ちます。保険をかけない場合の期待値は (4/13)*0 + (9/13)*(1.5) = 13.5/13 = 1.0384615 となり、1.0 よりも大きくなります。したがって、保険やイーブンマネーを辞退してハンドをプレイする方が得策です。デッキの数が有限である実際のゲームでは、10 が 1 つデッキから (あなたの手札に) 既に出ているため、ディーラーがブラックジャックを持っている確率が低くなり、オッズはさらに高くなります。
「賭けを二分してはならない」――賭博の十戒(第7)
マイクへ。ラスベガスへの私の最後の旅行で私が出会ったディーラーは、8枚のカードのうち5枚だけがディーラーに自動勝利を与え、彼はディーラーの7に対して16でのスタンドという「考えをいじって」いました。この戦略はどのように行われるのですか?
それは悪いプレイになります。例えば、私の ブラックジャック別表9B ではディーラー7に対して10と6のカードをプレイすることで双方向のリターンを示しています。ヒットするとベットの39.6%の損失が予想されますが、スタンドでは47.89%の損失が予想されます。ヒットが優れている理由を簡単に説明することはできませんが、発生する可能性のある全てを考慮しその確率で重み付けをして合計をとる必要があります。
お褒めいただきありがとうございます。Unified Gamingのブラックジャックでは、ディーラーが10を出している場合のみ、付録6を使用してください。ディーラーがエースを出している場合も、Unified Gamingの基本戦略には例外はありません。
コスタリカから帰ってきたばかりです。ブラックジャックはイーブンマネーで配当が支払われます。これはハウスにとってどれくらいの価値があるのでしょうか?ディーラーが3-6で21だった場合、配当は1対1なので、ダブルダウンすべきでしょうか?
コスタリカで人気のあるブラックジャックの一種であるラミーに関する私のページをご覧ください。
こんにちは。マイクロゲーミングのブラックジャックの基本戦略カードを確認しました。7と7の場合、10に対してヒットしないようアドバイスされているのに気づきました。なぜでしょうか?また、14で10に対してヒットするというアドバイスは、このアドバイスよりも優先されるのでしょうか?
これは、私がシングルデッキで展開するブラックジャックの戦略において、常に正しいプレイです。なぜなら、3枚目の7が出る確率はわずか2/49、つまり約4.08%だからです。ダブルデッキでは6/101 = 5.94%です。ディーラーの20に勝てる可能性は低いので、ヒットするか、可能であればサレンダーする方が賢明です。もちろん、これは10に対して14でヒットするという私のアドバイスよりも優先されます。
私はディーラーを10年間務めてきましたが、そこから抜け出そうと努力しています。「常に10が隠れていると想定しろ」という話を何度聞いたことか。あなたも私も、これが常に正しいとは限らないことは分かっています。なぜそう言われるのかは理解できますが、本当に10である確率はどれくらいでしょうか?ディーラーがエースを出し、カードリーダーでブラックジャックをチェックしてもブラックジャックがない場合は、10ではないことは間違いありません。では、何だと想定すればいいのでしょうか?
私もその表現は好きではありません。せいぜい、ディーラーが7~10の数字を持っている場合にスティッフハンドをヒットすることを覚えさせるための記憶手段に過ぎません。あらゆる状況に当てはまる簡単な経験則などありません。
ブラックジャックのサイトで付録1を勉強していたら、奇妙な点に気づきました。6デッキゲームの基本戦略(スプリット後にダブル、ディーラーはソフト17のままなど、ストリップの通常のルール)では、ディーラーが5を持っている場合、A,2はダブルダウンとされています。ところが、付録によると、プレイヤーの期待リターンはダブルよりもヒットの方が高くなっています(ヒットの場合は0.1334、ダブルの場合は0.126)。ディーラーが4を持っている場合も同様です(ヒットの場合は0.0593、ダブルダウンの場合は0.0584)。その他のスプリットとダブルはすべてうまくいきます。この2つの例はどうなっているのでしょうか?よろしくお願いします。
付録1は無限デッキに基づいています。あなたが挙げたどちらのハンドも境界線上のプレイであり、デッキの数によってどちらのプレイが優れているかが変わります。例えば、A-4対4の場合、26デッキならダブル、27デッキならヒットが有利です。A-2対5の場合も、8デッキと無限デッキの間を行き来します。
私はブラックジャックプレイヤーとして、10をスプリットしてバストカードと対戦することがよくあります。この動きは期待値がプラスですが、スタンディングパットほど利益は上がりません。ニュートラルデッキで10をスプリットすることがスタンディングパットよりどれだけ悪いのか、この友人に教えていただけませんか?また、多くのブラックジャックプレイヤーは、10を6とスプリットする人に腹を立てますが、彼ら自身も2や7を10とスプリットすることが多いのです。この点について、正しい情報を提供してもらえますか?
このような疑問に答えるために、ブラックジャックの付録9A~9Hを作成するのに苦労しました。例えば、ディーラーがソフト17でスタンドする6デッキゲームでは、ブラックジャックの付録9Gを使用します。そこには、ディーラーが6に対して10が2枚スタンドした場合の期待リターンが0.702826であることが示されています。この状況でスプリットした場合の期待リターンは0.622165です。つまり、スプリットではなくスタンドすることで、プレイヤーは8.07%の追加勝利を期待できるということです。ブラックジャックのテーブルで他のプレイヤーの発言や行動をあまり鵜呑みにしないでください。
ウィズさん、ディーラーが10を持っている場合の8のスプリットについて質問です。シングルハンドではスプリットが正しいプレイです。しかし、一般的なブラックジャックプレイヤーであれば、賭け金を倍にすることを考えると、スタンドする方が良いと思います。なぜ、平均をはるかに下回る低いオッズで賭け金を倍にするのでしょうか?結局のところ、目標は全体的なリターン(つまり、すべての賭け金の加重平均)を最大化することなのです。ご意見をお聞かせください。
PS あなたのサイトは素晴らしいですし、バナー広告やサイドバーのような広告は理解できますが、ポップアップウィンドウや質問プロンプトのような侵入的な広告は、別のサイトへ強制的に誘導しようとするので、ちょっとやりすぎだと思います。
これは僅差のプレイですが、スタンドは3番目に悪い選択肢です。私のブラックジャック付録9Gを使用すると、期待リターンは以下のようになります。
- スタンド -.536853
- ヒット -.535361
- スプリット -.474733
- ダブル -1.07022
スプリットは、ハンド全体の損失を最小限に抑えられるため、最善の判断です。ダブルとスプリットの期待リターンは、そのハンドのトータルリターンと最初のベット額の比率に基づきます。例えば、最初のベット額が100ドルで、8をスプリットした場合、すべての要素を考慮した期待損失は47.47ドルとなり、スタンドした場合の期待損失53.69ドルよりも低くなります。
ダブルエクスポージャーのチャートでは、ディーラーが13~16の場合、10をスプリットするように示されています。これは、10がさらに増えてもスプリットし続けるという意味ですか?私は実際にそうしたことがあり、18未満のハンドが4つありましたが、すべて負けました。幸い、当時はインターネットのゲームサイトで遊び半分でプレイしていたので、その点は良かったです。
はい、10が出続ける限り、スプリットを続けるべきです。片方のハンドをプレイして負けたからといって、何も否定されるわけではありません。本当にベストなプレイを知るには、何百万ものハンドを両方の方法でプレイし、その結果を集計する必要があります。
4デッキのブラックジャックで、5または6に対してエースをスプリットし、もう1枚エースが出た場合、ダブルとヒットのどちらが良いでしょうか?(現時点ではスプリットはもうありません)サイトによって回答が異なります。今のところ、5と6でダブルするとしているサイトもあれば、6でのみダブルするとしているサイトもあり、他のサイトでは全てのケースでスプリットを記載しており、おそらくこの状況を考慮していないのでしょう。また、4デッキのブラックジャックで10、2対4のゲームで、あるサイトではヒットと記載されていました。確認させてください。
ほとんどのカジノではどちらも許可されないことを覚えておいてください。ただし、可能であれば、6 の場合にのみダブルダウンするべきです。これは、ディーラーがソフト 17 をヒットするかどうかに関わらず当てはまります。ディーラーがソフト 17 でスタンドした場合、5 に対してヒットすると期待されるリターンは .162849、ダブルすると .148228 となるため、ヒットする方がよいプレイです。6 に対しては、ヒットすると期待されるリターンは .189020、ダブルすると .196249 となるため、ダブルダウンする方がよいプレイです。これらの数字は、私のブラックジャック付録 9eで確認できます。他の質問については、はい、4 デッキ ゲームでは、プレイヤーは 4 に対して 10、2 をヒットする必要がありますが、ディーラーがソフト 17 でスタンドした場合のみです。4 デッキの基本戦略の例外については、数が少なく、影響が小さいため、私はリストしていません。この例外に従うことで、113396ハンドごとにより多くのユニットを獲得できるようになり、ハウスエッジを0.000882%下げることができます。ただし、この例外を記憶する手間をかける価値はないと個人的には思います。
これは興味深い状況です。シングルデッキで10に対して15で5/6の確率で降参すべきですが、常に降参するよりも常にヒットする方が良いでしょう。以下は、15を組むために各方法でヒットした場合の期待リターンです。
- 10+5
- -.501091
- 9+6
- -.509827
- 8+7
- -.474794
10+5の組み合わせは4通りあり、他の2通りはそれぞれ1通りしかありません。つまり、シングルデッキで10に対して15をヒットした場合の全体的な期待リターンは、(4/6)*-.501091 + (1/6)*-.509827 + (1/6)*-.474794 = -.498164となります。つまり、10、5、9、6の場合はわずかに降参するオッズが有利ですが、8、7の場合ははるかに大きな差で有利です。8、7の方が期待リターンが高いのは、5と6がすべてデッキに残っているため、合計が20または21になる可能性が高くなるためです。
BJのテーブル最大ベット額について質問があります。例えば、上限額が200ドルだとします。200ドルベットして、8-3のカードが配られました。ダブルダウンはできますか?それとも既に上限額に達しているのでしょうか?あるいは、200ドルベットして、エースのペアが配られたとします。これをスプリットして、1つのハンドを2つのハンドにすることはできますか?
はい、そのような状況ではダブルまたはスプリットが可能です。上限は最初のベットに適用されます。上限が200ドルであれば、200ドルのハンドを複数回プレイすることもできます。
マルチデッキ(4デッキ以上)のブラックジャックで、ディーラーが10を持っている場合、4または5を含むマルチカード16でスタンドするのが正しい基本戦略だと書かれた記事を読みました。ウェブサイトを確認したところ、1デッキと2デッキのゲームにおけるマルチカードハンドに関する付録しか見つかりませんでした。この記事は正しいでしょうか?
はい!いい質問ですね。私も知りませんでした。デッキ数が少なく、カードの枚数が多いほど、この傾向は強くなります。ヒットに有利になる可能性が最も高い、デッキ数8でカードが3枚だけのケースをテストするために、あらゆる状況を想定した組み合わせプログラムを実行しました。次の表に結果を示します。
8デッキゲームにおける3枚16対10の期待値
| 手 | EVヒット | EVスタンド | 最高 遊ぶ | 確率 | 戻る 打つ | 戻る 立つ |
| 2010年1月5日 | -0.540978 | -0.539872 | 立つ | 0.132024 | -0.071422 | -0.071276 |
| 1/6/9 | -0.536558 | -0.540151 | 打つ | 0.059837 | -0.032106 | -0.032321 |
| 1/7/8 | -0.537115 | -0.537003 | 立つ | 0.059837 | -0.032139 | -0.032133 |
| 2010年2月4日 | -0.540947 | -0.541 | 打つ | 0.237478 | -0.128463 | -0.128475 |
| 2009年2月5日 | -0.542105 | -0.540534 | 立つ | 0.039891 | -0.021625 | -0.021563 |
| 2/6/8 | -0.537701 | -0.540773 | 打つ | 0.059837 | -0.032174 | -0.032358 |
| 2/7/7 | -0.538271 | -0.537584 | 立つ | 0.028983 | -0.015601 | -0.015581 |
| 2010年3月3日 | -0.540385 | -0.540995 | 打つ | 0.115028 | -0.06216 | -0.06223 |
| 3/4/9 | -0.541769 | -0.540536 | 立つ | 0.059837 | -0.032418 | -0.032344 |
| 3/5/8 | -0.54295 | -0.540022 | 立つ | 0.039891 | -0.021659 | -0.021542 |
| 3/6/7 | -0.538575 | -0.540228 | 打つ | 0.059837 | -0.032227 | -0.032326 |
| 4/4/8 | -0.543188 | -0.54003 | 立つ | 0.028983 | -0.015743 | -0.015652 |
| 4/5/7 | -0.544396 | -0.539483 | 立つ | 0.039891 | -0.021717 | -0.021521 |
| 4/6/6 | -0.539446 | -0.542878 | 打つ | 0.028983 | -0.015635 | -0.015735 |
| 5/5/6 | -0.545033 | -0.542137 | 立つ | 0.009661 | -0.005266 | -0.005238 |
| 合計 | 1 | -0.540355 | -0.540293 |
一番下の行の右側の2つの数字は、ヒットした場合の全体的な期待値が-0.540355、スタンドした場合の期待値が-0.540293であることを示しています。つまり、スタンドの方がわずかに有利なプレイです。このルールに従うと、1117910ハンドごとに1ユニットの追加利益が得られます。このアドバイスによってプレイヤーが1ユニット節約できるようになるまで、週40時間ブラックジャックをプレイして約5年かかります。
オンラインシングルデッキブラックジャックのプレイを微調整するために、ブラックジャックの付録3をよく使っています。12月にこのページが更新されたようですが、2カードセクションにいくつか新しい動きがあるようですね。4に対して10&2をヒットするというアドバイス、特にディーラーがバストする可能性が高い6に対しては、ヒットするべきだというアドバイスが理解できません。また、これらのカードはヒットするのが正解なのに、5に対して10&2をヒットするのはダメなのでしょうか?この点について、何かご意見があれば教えていただけると嬉しいです。重要なのは、ディーラーが6でAをホールインできるかどうかということでしょうか?うーん、それはあり得そうです。これらは新しい戦略ですか?もしそうなら、なぜ生まれたのでしょうか?
はい、2枚のカードのリストにいくつか変更を加えました。9+3対3を削除し、10+2対6を追加しました。ディーラーがソフト17でスタンドし、プレイヤーが10+2でディーラーが6の場合、シングルデッキゲームでは、ヒットの期待値は-0.159436、スタンドの期待値は-0.160379です。つまり、ヒットする方が平均的に損失は少なくなります。カードの展開は無数にあるため、基本戦略について簡潔な回答をするのは難しいです。ディーラーがバストする確率は6の方が高くなります。しかし、おっしゃる通り、ディーラーは5よりも6が出ている方が17になる可能性が高くなります。17は良い手ではないので、プレイヤーはヒットして負けまいとします。
もしあなたが15を持っていて、ディーラーが8を出していたとしたら…基本戦略はヒットです。この場合、ヒットしてもステイしても負ける確率は70%を超えます…ヒットしてもステイしても70%以上の確率で負けるなら、なぜサレンダーする方が良いプレイではないのでしょうか?
話を単純にするために、あなたの例に倣い、ヒットした場合の勝率を70%、負け率を30%としましょう。ヒットした場合の期待値は0.3*1 + 0.7*-1 = -0.4となります。これは、降参した場合の期待値-0.5よりも大きいです。
MicrogamingのシングルデッキゲームA,A vs Aで、基本戦略カードに示されているようにスプリットするのが正しいプレイなのか確認したかったんです。少なくとも4デッキならヒットするのが正解だと思います。ただ、10が全部残っていると、賭け金の2倍の負けになることが多いような気がします。あなたの言うことを信じていないわけではなく、ただ確認したかっただけです。このハンドでヒットとスプリットのEVは分かりますか?
この件については何度か質問を受けてきましたが、トータルベットを失うにもかかわらず、エースをスプリットするためにドローする選択肢はヨーロピアン・ノーピーク・ルールを回避できるため、スプリットの方がより良いプレイだと主張し続けています。1デッキを基準に、各ハンドの期待値(ディーラーがブラックジャックになる可能性を考慮)は、ヒットで-0.532849、スプリットで-0.223277です。つまり、スプリットの方が約31%有利です。また、4デッキゲームでもスプリットの方が有利ですが、同じルールの1デッキゲームが存在するため、Microgamingのプレイヤーは4デッキゲームをプレイすべきではありません。
あなたと同じルール(ディーラーは17をすべてスタンド、エース以外の4ハンドまで再スプリット可能、エースは1回のみスプリット可能、スプリット後はダブル、エースのスプリットは1枚のみ)でブラックジャックの無限デッキ分析を行った後、あなたのサイトを見つけました。期待値を比較したところ、ペアスプリットを除いて全てのケースであなたと同じ値が得られました。ペアスプリットは若干異なりました。そこで、スプリットの期待値をどのように計算したのか教えていただけますか?
ペアのスプリットを正しく理解するのに、私自身も何年もかかりました。Gambling ToolsのCindyさんはとても助かりました。Peter Griffin氏も『The Theory of Blackjack』の第11章でこのトピックについて触れています。例えば、ディーラーが2ハンドの場合に8ハンドをスプリットした場合の期待値を調べたいとします。リスプリットは最大4ハンドまで可能です。私が行った方法は以下の通りです。
- 靴から 2 と 8 を 2 つ取り出します。
- プレイヤーがどちらの手でも 3 つ目の 8 を出さない確率を決定します。
- 8以外のすべてのランクを調べ、デッキからそのカードを引き、そのカードと8のカードをプレイし、期待値を求め、2倍します。各ランクについて、そのランクの確率を求めます。ただし、他の8の確率は0です。各ランクの確率と期待値の内積を求めます。
- このドット積に手順 2 の確率を掛けます。
- プレイヤーが 3 つのハンドに再分割する確率を決定します。
- デッキからさらに 8 枚を取り出します。
- 手順 3 を繰り返しますが、2 ではなく 3 を掛けます。
- ステップ 7 のドット積にステップ 5 の確率を掛けます。
- プレイヤーが 4 つのハンドに再分割する確率を決定します。
- 靴からさらに 8 を 2 つ取り出します。
- 手順 3 を繰り返しますが、2 ではなく 4 を掛けます。今回は、プレイヤーが再分割を停止せざるを得ない状況に対応して、3 枚目のカードとして 8 を取得することを検討します。
- ステップ 11 のドット積をステップ 9 の確率で乗算します。
- 手順 4、8、12 の値を追加します。
この中で一番難しいのはステップ3です。確率木を使って決定する長い式がぎっしり詰まった、とても見苦しいサブルーチンを作っています。ディーラーが10かエースを持っていると、特に見苦しくなります。
一般的にソフト17はディーラーに有利だというのはその通りです。しかし、これは一般論であり、すべての状況に当てはまるわけではありません。18~21の強いハンドを持っている場合、ディーラーにはソフト17でスタンドしてもらいたいものです。一方、17未満の弱いハンドを持っている場合、ディーラーにはソフト17でスタンドしてもらいたいものです。戦略の違いの例として、ディーラーがソフト17を出した場合は6に対してソフト19をダブルし、ディーラーがソフト17でスタンドした場合はスタンドする、というものがあります。これは、ダブルで悪いカードを引いて16点以下になる可能性が高いためです。ディーラーがソフト17を出した場合はバーストする確率が高くなるため、この例ではダブルの方が少し安全です。
クラップスで儲ける方法を既に教えていただき、ありがとうございます!今度はあなたのサイトでブラックジャックを学んでいます。一つ質問があります。例えば、5が2枚あってダブルダウンしたい場合、最初のベットに加えて追加のベットを置くように言われますよね。ディーラーはどうやってスプリットするつもりがないとわかるのでしょうか?ありがとうございます!あなたのサイトは最高です!
お褒めいただきありがとうございます。ディーラーはご質問にお答えするために、ただご希望をお伺いするだけです。ブラックジャックでは通常、すべての決定は目に見えるようにしなければなりませんが、これは私が思いつく唯一の例外です。ただし、自分の番になった時に聞かれたくない場合は、人差し指を立ててカードを1枚欲しいことを示すだけで結構です。ほとんどのディーラーはこれが何を意味するのか理解しています。偶然にも昨日、ブルガリアではダブルベットをしたい場合は追加のベットを元のベットの後ろに置き、スプリットをしたい場合は元のベットの隣に置けることを知りました。
別の読者は、ノースダコタ州では、倍増と分割についてはブルガリアのルールに従うのが州法であると書いていました。
ブラックジャックの基本戦略チャートには、ディーラーが3-6を持っている場合、A、7で「ダブルダウンが可能な場合はダブルダウン、そうでない場合はスタンド」と書いてあります。質問なのですが、なぜスタンドするのでしょうか?ダブルダウンしたいのにできないなら、少なくともヒットできるならヒットすべきではないでしょうか?いずれにしてももう1枚カードを受け取るつもりだったのに。お時間をいただき、ありがとうございました!
プレイヤーが賭け金を倍にしてスタンドする選択肢があれば、従来のダブルよりも有利になります。つまり、このような場合、カードを引くことは実際にはプレイヤーの手札にとって不利ですが、2倍の金額を賭ける価値はあります。
ブラックジャックの基本戦略チャートでは、ディーラーがエースを出している場合は16でヒットすると書かれています。このチャートは、インシュランスが支払われないことが分かれば、ディーラーが10の価値を持つカードを伏せていないという事実を考慮しているのでしょうか?明らかにディーラーがハンドを完成させる可能性は低くなりますが、プレイヤーが16でスタンドするだけで十分なのでしょうか?
はい、基本戦略ではディーラーが10を持っていないことを前提としています。ディーラーがチェックしないヨーロッパでも、ヒット/スタンド戦略は同じです。なぜなら、ディーラーがブラックジャックを持っている場合、プレイヤーはいずれにせよ望みがないからです。ディーラーがエースを持っている場合、ブラックジャックではないと仮定すると、ソフト17でディーラーがスタンドした場合、17以上になる確率は83.3%です。つまり、スタンドはそれほど危険なプレイではなく、オッズは明らかにヒットに有利です。
ディーラーが 10 が表示されてもブラックジャックかどうか確認せず、ハンド終了時に元の賭け金のみを取る場合、戦略の変更は必要でしょうか?
いいえ。元の賭け金だけを失うのであれば、ディーラーがブラックジャックを持っていないと仮定してプレイすべきです。もしディーラーがブラックジャックを持っていたら、どうすることもできません。
プレイヤーは保険を拒否すべきだという数学的な議論は有効です。しかし、心理学的な議論は有効ではありません。ほとんどの人は、手持ちの鳥を1羽手放して藪の中の鳥1.5羽を逃すのは愚かだと感じるでしょう。
おい。ギャンブルとはリスクを取ることだ。成功するギャンブラーは、毎回の純利益の確率を最大化しようとはせず、全体的なリターンを最大化するためにリスクを取る。ギャンブルでも人生でも、長期的な利益を得るためには、時には短期的なリスクを負わなければならない。だから、今のことよりも未来のことを考えるべきだ。
ブラックジャック スイッチの基本戦略表に、常に 12 でヒットするように記載しているのはなぜですか?
ブラックジャックスイッチでは、ディーラーが22になるとプッシュになるため、プレイヤーはより積極的にヒットする必要があります。通常のブラックジャックでは、スタンドの価値の多くはディーラーがバストしたときに発揮されます。ブラックジャックスイッチでは、そうした勝利の多くがプッシュに変わるため、ヒットする方がより良いプレイとなります。
妻はブラックジャックの基本戦略は知っているのに、どうしても「勘」でプレイしたいと言います。妻が勘に頼るプレイを50-50に最も近いハンドに限定できるよう、どのようなハンドを選べば良いでしょうか?
すでに回答が出ていると思いますが、良い質問なのでもう一度回答させていただきます。カードカウンティング指数がゼロであることからもわかるように、境界線上のプレイをいくつか挙げています。このリストは、ディーラーがソフト17でスタンドし、スプリット後にダブルが認められる複数のデッキを対象としています。最初に最善のプレイ、次に代替プレイを挙げています。
- 9対2(ヒット/ダブル)
- 12対4(スタンド/ヒット)
- 12対6(スタンド/ヒット)
- 16対10(ヒット/スタンド)
- ソフト13対5(ダブル/ヒット)
- ソフト15対4(ダブル/ヒット)
- 3、3対2(スプリット/ヒット)
ブラックジャックのセクションを隅々まで調べたのですが、サレンダーの「やり方」がわかりません。サレンダーのやり方は分かっているのですが、チップの半分を取ればそれで終わりなのでしょうか?
いいえ、ベットしたらハンドが終わるまでチップに触ってはいけません。サレンダーの合図は、人差し指を使って、ブラックジャックのテーブルに沿って、ベットした場所のすぐ後ろの左から右へ線を引くふりをすることです。最近ヨーロッパの友人がテーブルで実際にそうするまで、私はこのことを知りませんでした。ただ「サレンダー」と言うだけでも十分です。
理由は、ディーラーが22で、あなたの手札が21以下だった場合、プッシュされるからです。これはディーラーに非常に有利に働き、ダブルやスプリットでさらにお金を賭ける意欲を削ぐはずです。
先日、6:5のゲーム(またはリオのイーブンマネーゲーム)をプレイしている場合、ナチュラルが出たら配当の減少を補うためにダブルダウンすべきだと聞きました。これは正しいでしょうか?その場合の予想損失はいくらでしょうか?
これはひどいプレイです。例えば、ブラックジャックで5(6デッキのディーラーがソフト17でスタンド)に対してダブルした場合、私のブラックジャック付録9Iによると、期待利益は0.622362になります。つまり、たとえイーブンマネーゲームであっても、これは賭け金の約38%を失うミスとなります。
ウォンは『プロフェッショナル・ブラックジャック』の23ページで、「10-2または2-10(10は10カウントのカード)で12に達し、2デッキ以下(ディーラーがソフト17でスタンドする場合は7デッキ以下)でプレイしている場合はヒットすべきだ」と述べています。これは正しいでしょうか? 1デッキまたは2デッキのゲームでは、構成依存戦略がある程度の価値を持つので、この考え方は理解できますが、7デッキ(S17)でプレイしている場合は10-2/2-10をヒットすべきだと言っているのです! 私には正しく思えません。
ウォン氏は、ディーラーが4の手札に対してプレイヤーが12の手札を持っている状況について言及しており、ピーター・グリフィン著『ブラックジャックの理論』 176ページを引用しています。確かに、彼の言う通りです。7デッキのゲームでは、ヒットの期待値は-0.210820、スタンドの期待値は-0.211106なので、ヒットの方が高くなります。しかし、8デッキの場合、ヒットは-0.2111161、スタンドは-0.211100なので、スタンドの方が高くなります。これは、デッキ数が7と8では違いが出る、非常にギリギリのプレイです。さらに良い例を挙げましょう。A-4でディーラーが4の場合、26デッキまではダブルダウンしますが、27デッキ以上ではヒットします。
インターネットでのダブルやスプリットに関して、キャッシュバックがベット総額に適用される(つまり、プレイヤーにダブルやスプリットを行うインセンティブが加わる)場合、基本戦略の例外はありますか?キャッシュバック率は0.1%と仮定してください。
0.1%の差で戦略が変わるようなハンドは見つかりませんでした。6デッキでディーラーがソフト17でスタンドしている状況で最も近いのは、ディーラーが4に対してA4をプレイする場合です。このハンドでは、ダブルダウンはヒットに比べてプレイヤーの期待値が0.3%弱低下します。つまり、0.3%以上の差が出るのであれば、そのハンドをダブルダウンしましょう。私が調べた他のボーダーラインハンドでは、ダブルダウンやスプリットに少なくとも1%のコストがかかり、ブラックジャックでこれほど高いキャッシュバックは見たことがありません。
ブラックジャックでは、16 対 10 の戦略は R、S です。2 枚のカードのハンドを排除すると、戦略はデッキの数に関係なくスタンド (ヒットしない) になります。
一般的に、16対10で3枚以上のカードがある場合はスタンドすべきであることは事実です。したがって、私のチャートがカジノがサレンダーオプションを提供していることを前提としているのであれば、あなたの考えは正しいでしょう。しかし、その前提は正しくありません。もしキーをRs(サレンダーが許可されている場合はサレンダー、そうでない場合はスタンド)に変更すると、サレンダーが許可されていない場合、プレイヤーは10に対して2枚の16でスタンドすべきということになります。
ブラックジャックの付録9では、プレイヤーが10に対して10をヒットする確率がプラスであると示されていますね?例えば、6デッキでプレイヤーの10が6と4で構成されている場合、プレイヤーのアドバンテージは0.026796とされています。プレイヤーとディーラーは17になるまでヒットしないのでしょうか?これはディーラーに有利になるはずです。なぜなら、両方がバストした場合、ディーラーが勝つからです。
理由は、プレイヤーの次のカードはエースかもしれないが、ディーラーの次のカードはそうではないからです。付録の説明で、ディーラーはブラックジャックではないと既に想定していると述べました。そのため、ディーラーが覗いてブラックジャックではないことを確認した後、プレイヤーはわずかに有利になります。
ほとんどのブラックジャックのカウンティングシステムでは、10に対する16の指数は0です。つまり、デッキが完全にニュートラルであればスタンドすべきです。なぜなら、カウントが指数と等しいかそれを超える場合はスタンドするからです。しかし、基本戦略表ではヒットするように指示されています。これは矛盾しているように思えます。
正直に言うと、これは古い質問ですが、Chris F.さんからより良い回答をいただきました。彼は正しく、基本戦略チャートを作成する際に、プレイヤーの最初の2枚のカードとディーラーのアップカードは既にデッキから取り除かれているものと想定しているためだと説明しています。良い例として、シングルデッキでは、10に対して7,7でスタンドするのが正しいプレイです。デッキの7の半分はすでになくなっており、ディーラーの20を3枚のカードで倒すにはそれが必要なためです。
16対10の場合、プレイヤーの手札は10と6、または9と7のいずれかになります。いずれの場合も、ヒットすればプレイヤーをバストさせる2枚のカードが取り除かれています。そのため、デッキにはバストさせない小さなカードがやや多く含まれ、プレイヤーはヒットする動機が生まれます。これは事実ですが、無限デッキのゲームではヒットする確率が依然として高いため、私は懐疑的でした。しかし、一部のインターネットカジノを除いて、無限デッキは単なる抽象概念です。ディーラーがカードを1枚も配らずに「あなたは16で、私は10ですが、ブラックジャックではありません」と言った場合、8デッキのゲームでどのようなプレイが最善なのか興味がありました。gamingtools.net(サイトは既に存在しません)のブラックジャックアナライザーを使って、8デッキを入力し、6と10を除くすべてのカードを1枚ずつ、そして10を2枚ずつ慎重にデッキから取り除きました。その後、ディーラーに10、自分に10と6を出しました。つまり、プレイヤーはAから9までをそれぞれ31枚、10を124枚持つニュートラルデッキを相手にこのハンドをプレイしていたことになります。期待値は次のとおりです。
10+6対10 — 8つのデッキ
| 遊ぶ | 期待値 |
|---|---|
| 立つ | -0.5399 |
| 打つ | -0.5399 |
期待値は同じですが、アプレットはスタンドの方がより良いプレイとして強調表示しています。これはおそらく、小数点以下4桁を超える数値が大きいためです。以下の数字を削除して9,7対10をシミュレートしても、プレイヤーは全く同じニュートラルシューを相手にしているので、結果は同じです。
これは、8デッキのゲームでカードが3枚しかない場合でも、除去の効果がいかに強力であるかを示しています。元の質問に戻ると、ゼロカウントは、プレイヤーの2枚のカードとディーラーのアップカードを計算した後、完全にニュートラルなデッキを反映しています。つまり、ニュートラルデッキに入ると、先ほど示したように、スタンドする方が有利になります。無限デッキでヒットすることが正しい理由は、除去の効果がないためです。ニュートラルシューで誤って16対10をヒットし、低いカードが出た場合、ディーラーはホールカードに10を入れる可能性が高くなります。この事実は、8デッキのゲームでスタンドする期待値が高いことに反映されていますが、無限デッキでは問題になりません。記録のために、無限デッキのゲームでの期待値は次のとおりです。
10+6 vs 10 — 無限デッキ
| 遊ぶ | 期待値 |
|---|---|
| 立つ | -0.5404 |
| 打つ | -0.5398 |
ブラックジャックでは、ディーラーがホールカードを公開することがあります。そのような場合の正しい基本戦略は何ですか?
スタンフォード・ウォンは著書『ベーシック・ブラックジャック』の中で、このような基本戦略を紹介しています(表46参照)。また、1995年にラスベガスのバーボンストリート・カジノで、ディーラーが50分ごとに5ハンド分、両方のカードを公開するというプロモーションがあったと述べています。ウォンによれば、このプロモーション中のプレイヤーの優位性は約10%でした。
分割後に基本戦略の例外を使用する必要がありますか?
いい質問ですね。個人的には、既にプレイされた内容、特に2手目の内容に基づいて、境界線のプレイを目分量で判断します。強いて言えば、基本戦略のみよりも例外戦略を使う方が良いでしょう。ただし、基本戦略の例外戦略は最初の手のみに適用されているため、デッキ構成が多少異なるため、スプリット戦略としては完全に正確とは言えません。
あなたのブラックジャックの戦略カードの構成は、最初のカード(プレイヤーの最初の2枚のカードとディーラーのアップカード)の基本的な戦略だと思います。ただし、ヒットまたはスプリット後にデッキ構成が変更されることで、その基本戦略が変わる可能性があります。私がより適切だと思うのは、スプリットとヒットの後を含んだブラックジャックの全体的なゲームに基づく基本的な戦略です。最初の手の基本戦略とゲーム全体の戦略が異なる状況はありますか?
その通りです。私の基本的な戦略チャートは最初の2枚のカードに基づいて最高のプレイになるように設計されています。これは基本戦略を開発するための通常のアプローチであり、このアプローチのメリットとの1つとしては、各プレイの期待値を正確に計算して他のソースと比較できることです。ただし有効なポイントを提示します。そこで、Blackjack Attack の作者であるドン・シュレジンジャーに、ブラックジャックのゲーム全体の期待値を最大化するために、最初の手でのベストプレイがベストプレイと異なる既知のプレイがあるかどうかを尋ねました。彼は、ディーラーがソフト17のスタンドかつダブルデッキゲームでディーラーエースに対するソフト18はそのようなプレイであると答えました。私の ブラックジャックの別表9 が示しているように、立っている場合の期待値は-0.100502であり、打つ場合の期待値は-0.100359です。したがって最初の2枚のカードに基づくと、オッズは0.000143のヒットを支持します。ただし、ソフト18を表示する方法はエース1つと7つよりも多くあります。次の表は、この手が上がることができる全ての方法を示しています。
ソフト18 Vs エースの組み合わせの解析
| プレイヤー カード |
条件付き 確率 |
ヒット EV |
スタンド EV |
ヒット リターン |
スタンド リターン |
| A7 | 0.621139169 | -0.100359 | -0.100502 | -0.062336906 | -0.062425729 |
| A6A | 0.036728229 | -0.11202 | -0.116009 | -0.004114296 | -0.004260805 |
| A52 | 0.146912917 | -0.111299 | -0.103382 | -0.016351261 | -0.015188151 |
| A43 | 0.146912917 | -0.114804 | -0.103721 | -0.01686619 | -0.015237955 |
| A5AA | 0.001827682 | -0.111395 | -0.105122 | -0.000203595 | -0.00019213 |
| A42A | 0.016814677 | -0.116975 | -0.108233 | -0.001966897 | -0.001819903 |
| A33A | 0.007356421 | -0.132142 | -0.107256 | -0.000972092 | -0.00078902 |
| A322 | 0.020470041 | -0.134229 | -0.11004 | -0.002747673 | -0.002252523 |
| A4AAA | 0.000073486 | -0.117554 | -0.110984 | -0.000008639 | -0.000008156 |
| A32AA | 0.001028802 | -0.134775 | -0.112433 | -0.000138657 | -0.000115671 |
| A222A | 0.000709873 | -0.136788 | -0.114993 | -0.000097102 | -0.00008163 |
| A3AAAA | 0.000002238 | -0.135313 | -0.114821 | -0.000000303 | -0.000000257 |
| A22AAA | 0.000023502 | -0.137312 | -0.117376 | -0.000003227 | -0.000002759 |
| A2AAAAA | 0.000000046 | -0.137859 | -0.119823 | -0.000000006 | -0.000000006 |
| Total | 1 | -0.105806844 | -0.102374694 |
列のタイトル説明
プレイヤーカード:プレイヤーの手札にあるカード
条件付き確率:プレイヤーがディーラーエースに対してソフト18を持っているとすると仮定して与えられた手を構成する確率
ヒットEV:ヒットによる期待値
スタンドEV:スタンドによる期待値
ヒットリターン:確率とヒット期待値の積
スタンドリターン:確率とスタンド期待値の積
下の行の右の2つのセルは、全体的なヒットの期待値が-0.105807でスタンドしている場合の期待値が-0.102375であることを示しています。したがって、この表は0.00343までのオッズの支持を示しています。
これらの結果を確認するために、問題のルール下で2つのシミュレーションを実行しました。1つはヒットしてもう1つはスタンドしています。プレイ中のディーラーエースに対してソフト18が起こった手だけを数えました。以下がその結果です。
ソフト18 Vs エースシミュレーション
| ソフト17 | プレイ された手 |
合計 勝利数 |
期待値 |
| スタンド | 3857490 | -396224 | -0.102715 |
| ヒット | 3208390 | -337572 | -0.105215 |
したがってこのシミュレーションは、これらの手が現れる全ての可能なシナリオよりも0.0025の期待できるオッズを示しています。これら全ての手をプレイするという実用的な目的のために、私の基本的な戦略チャートが言っていることに反して最も良いプレイはスタンドすることです。
こんにちは。偶然あなたのサイトを見つけました。ブラックジャックの情報を得るのに素晴らしいサイトだと思います。ただ、一つ質問があります。基本戦略に従い、ディーラーが10またはエースを出している場合(ディーラーがブラックジャックではない場合)、合計が10のときに期待値がプラスになるのはなぜでしょうか?あなたの表ではどちらのシナリオでも期待値がプラスになっているようですが、その理由が理解できません。このシナリオでは、プレイヤーとディーラーは同じ戦略、つまり17以上になるまでヒットするか、バストするまでヒットする戦略をとっていると思います。このシナリオでは、プレイヤー側のソフト17は排除されているので、期待値がプラスになる理由が理解できません。
温かいお言葉ありがとうございます。6デッキを想定してみましょう(ディーラーがソフト17でヒットするかスタンドするかは関係ありません)。私のブラックジャック付録9では、6+4でエースが出た場合の期待値は+0.081336、6+4で10が出た場合の期待値は+0.026796と示されています。期待値が正になっているのは、私の期待値表ではディーラーが既にブラックジャックを覗き込み、ブラックジャックではないことを確認していると仮定しているからです。一方、プレイヤーはまだエースを引いて21になる可能性があります。つまり、プレイヤーは次のカードで21を作ることができますが、ディーラーは仮定上21を作ることができません。もし私がヨーロピアンノーピークルールでこのような表を作成した場合、期待値は確かに負の値になるでしょう。
先日ラスベガスに行った際、2人のディーラー(1人はThe Orleans、もう1人はCircus-Circus)がそれぞれ独立して、4-4対6でスプリットではなくダブルを勧めているのを見ました。私はグループの中でBJ担当だったので、友人たちがそのことについて尋ねてきました。私はただ「いいえ、スプリットが正しい判断です」としか答えられませんでした。(もちろん、スプリット後のダブルが認められている場合ですが。)これらの選択肢の確率を調べたり、教えていただけませんか?よろしくお願いします。
以前にも言いましたが、ディーラーは集団として尊敬しているものの、彼らは間違ったアドバイスや誤った情報を多く与えています。5や6に対して4をスプリットするのはよくあるプレイですが、プレイヤーとディーラーの両方が誤ってスプリットを非難しています。「Fで始まるカード」、つまり4、5、そしてフェイスは絶対にスプリットしてはいけないという誤った意見を耳にすることがあります。5とフェイスについては確かにその通りですが、スプリット後にダブルが認められているのであれば、4は5や6に対してスプリットすべきです。そうでない場合はヒットすべきですが、シングルデッキの場合はダブルが認められている限りダブルすべきです。私のブラックジャックの付録9には、6デッキのゲームでディーラーがソフト17をヒットした場合、6に対して4と4の期待値が以下のように示されています。
スタンド: -0.114085
ヒット: + 0.113365
ダブル:+ 0.092929
分割: +0.207228 (分割後にダブル可能)
分割: + 0.056954 (分割後のダブルは許可されません)
ウィザードさん、ラスベガス旅行の準備であなたのサイトを拝見しています。最高のギャンブルサイトですからね。 2001年12月4日のコラムで、 16とディーラーの10でスタンドするタイミングについて分析されていたのが興味深かったです。私自身も数学が得意なので、オッズを最大化したいのですが、利益がわずかしかないことも理解しています。多くのベーシックストラテジープレイヤーと同じように、私は2、3、4、5を持っている時は、ディーラーが10の時でも常に16をヒットしています。この件について教えていただいたので、ちょっと気になっているのですが、「5年に1ユニット」の利益を得るためにプレイを変えたのですか?それとも、毎回16をヒットすることにこだわっているのですか?いつもありがとうございます!
親切なお言葉、ありがとうございます。カウンティングではなく基本戦略でプレイする場合、すでに手札に4か5がある場合はスタンドする傾向があります。他のプレイヤーと表向きのゲームの場合は、テーブルをスキャンして最善の判断を下します。
ディーラーが両方のカードを公開するブラックジャック(付録 16 )では、8 のペアはディーラーの合計が 10 または 11 の場合にスプリットされません。代わりに、10 の場合はヒット、11 の場合はスタンドとされます。これは、ディーラーの 10 またはエースに対して 8 をスプリットする通常の BS とどう違うのでしょうか。
通常のブラックジャックでは、ディーラーが10またはエースを表向きにしている場合、プレイヤーは8をスプリットするべきです。しかし、ディーラーが誤って両方のカードを表向きにし、合計が10または11になっている場合、プレイヤーは10に対してヒットし、11に対してスタンドする必要があります。ディーラーが10またはエースを表向きにしている場合、プレイヤーの番が来る頃にはディーラーがブラックジャックではないことが分かるからです。なぜなら、ディーラーはホールカードを見て確認しているからです。そのため、プレイヤーはよりアグレッシブにプレイできます。しかし、ディーラーのカードが両方とも表向きにされ、合計が10または11になっている場合、ディーラーは10にエース、または11に10を引いて合計21になる可能性があります。そのため、プレイヤーはより慎重にプレイするべきです。
カードの除去とディーラーのアップカードとを混同されているようです。以下の表は、ディーラーがブラックジャックを確認する前の、ディーラーがソフト17とインフィニットデッキでスタンドした場合の、ディーラーのアップカードのみに基づくプレイヤーの期待値を示しています。
ディーラーのアップカードによる期待値
| アップカード | 期待される 価値 |
| 2 | 9.10% |
| 3 | 12.38% |
| 4 | 15.85% |
| 5 | 19.65% |
| 6 | 23.40% |
| 7 | 14.40% |
| 8 | 5.82% |
| 9 | -4.06% |
| 10 | -17.36% |
| あ | -33.78% |
したがって、ディーラーにアップカードとして6を選ぶことができるなら、それは6を選ぶべきであるというのは確かに真実です。6はディーラーにとって不利であるだけでなく、プレイヤーにとっても不利です。総合的に考えると、シューから1枚カードを取り除けるなら、5を選ぶべきです。
素晴らしいサイトですね!ブラックジャックの戦略カードは今まで見た中で最高です。どこかで入手できるでしょうか?今使っているカードにはサレンダーの要素がないのですが、これを使うことで何か損をすることがあるのでしょうか?
ありがとうございます。ほとんどのカジノのギフトショップで基本戦略カードが売られていますが、なぜかサレンダーのタイミングが書かれていません。サレンダーすべき状況はそれほど多くありませんが、よくあるので覚えておく価値はあると思います。6デッキゲームでは、ディーラーがソフト17でスタンドした場合、サレンダーの配当は0.07%、ヒットした場合は0.09%です。
友人とラスベガスでプレイしていた時のことです。2デッキゲームで、プレイヤーの合計が10でディーラーが7の時にダブルダウンするのと、プレイヤーの合計が11でディーラーが10の時にダブルダウンするのと、どちらが統計的にオッズが高いかで大喧嘩しました。私は前者だと思っていました。
私のブラックジャック付録9は、まさにこのような疑問に応えるために作成されました。6デッキを想定した場合、私の表によると、8+2を7に対してダブルする期待値は0.396342です。8+3を10に対してダブルする期待値は0.176919です。つまり、おっしゃる通り、10対7の方がはるかに良い手札と言えるでしょう。
標準的な BJ ルールと完璧な基本戦略によれば、ダブルダウン ハンドの何パーセントが勝ち、プッシュし、負けると予想されますか?
ラスベガスストリップのリベラルなルール(6デッキ、ディーラーはソフト17でスタンド、スプリット後のダブル可、レイトサレンダー可、エースの再スプリット可)を前提とすると、最初の2枚のカードでダブルした場合の各結果の確率は以下のとおりです。ただし、スプリット後のダブルは含まれません。
友人が、最初のカードが6だと、2枚目とディーラーのアップカードを見ずに文句を言い始めます。2、3、4、5など(つまり、まともな2枚目のカード)が出る可能性もあるし、ディーラーが2から6(テーブルにとって良いカード)を出す可能性もあるので、待つべきだと思います。どう思われますか?2枚目やディーラーのアップカードを知らずに最初のカードが6だった場合、彼の勝率はどれくらい下がるでしょうか?それとも、友人はただの愚痴っぽいだけでしょうか?お時間をいただきありがとうございました。
私のブラックジャック付録14によると、最初のカードが6の場合、期待値は既に約-21%です。例えば、相手が100ドルベットした場合、ハンドを売却してベットする適正価格は約79ドルです。相手が不満を漏らしている隙に、適正価格の79セントよりも低い価格でハンドを売却することを提案してみてはいかがでしょうか。あまり有利になりすぎずに優位に立つには、75セントをお勧めします。
先週末、ブラックジャックをプレイしていた時のことです。ディーラーはトップに6を持っていたのですが、ダウンカードを隠す際に誤ってホールに3があることを見せてしまいました。私の右側のプレイヤーは15、私は11、左側のプレイヤーは12でした。ディーラーの合計ハンドが9であることを知っていたため、右側のプレイヤーはハンドをヒットし、10でバストしました。私はダブルダウンして2を得ました。左側のプレイヤーはハンドをヒットし、5で合計17になりました。ディーラーは9のハンドをオープンし、10で合計19になりました。ディーラーは、たとえ3のアンダーカードが見えていたとしても、ダウンカードを知らないかのようにハンドをプレイすべきだと言いました。この状況で3人全員に対してどう対処したかを教えていただきたいです。ブラックジャックをプレイし始めてからこのようなことは初めてです。アドバイスをお願いします。ありがとうございます!
私のフラッシュブラックジャックディーラー戦略は、ディーラーが誤ってホールカードを表向きにしてしまった場合の対処法を示しています。しかし、ほとんどのプレイヤーはそれを暗記していません。私も含めてです。今回のようなディーラーの2枚のカードの合計が9以下の場合は、ディーラーのアップカードが2枚のカードの合計であると仮定して、基本戦略を使うことができます。この経験則を用いると、3人のプレイヤー全員が正しくプレイしました。ディーラーの発言とは反対に、プレイヤーにはこのようなディーラーのミスから得た情報を利用する権利があります。私はディーラーのコメントを無視するだけでなく、彼がまた同じことをしてくれることを期待してプレイを続けたでしょう。
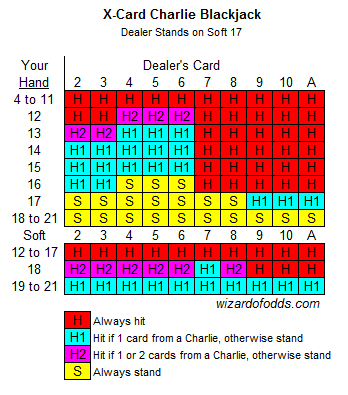
素晴らしいサイトを作成していただき、ありがとうございます。詳細な情報も掲載されています。ブラックジャックでは、様々なチャーリーカードでハウスエッジが大幅に減少すると書かれていますが、プレイ方法を変えるための提案は見当たりません。6デッキ以上の大きなシューで利益を最大化するために、ベーシックストラテジーの例外となるものはありますか?ディーラーがバストする可能性は非常に低いので、エースに対してチャーリーカードの1枚手前であれば、より多くのヒットを打つことになると思いますが、具体的な指示があれば教えていただけると嬉しいです。ありがとうございます。
どういたしまして。質問の意味がわからない読者のために説明すると、「チャーリー」とは、プレイヤーがバーストすることなく、一定枚数(通常は5~7枚)のカードをヒットした場合、自動的に勝利となるルールです。以下の表は、3枚以上のカードの場合で、プレイヤーがそのような自動勝利からあと1~2枚のカードしか離れていない場合の基本戦略を示しています。
多くのカジノでは、ブラックジャックのテーブルで他のプレイヤーの「ビハインド」ベットが許可されています。2人のプレイヤーが協力してベットする場合、「ビハインド」ベットが通常のベット額を大幅に上回る場合の適切なペアスプリット戦略を教えてください。
ご満足いただけましたでしょうか?この質問に答える新しいページを追加しました。ブラックジャックの付録19をご覧ください。
理由は、私のブラックジャックの基本戦略は8デッキ以下を前提としているのに対し、ディーラーのフラッシュ戦略は無限デッキを前提としているからです。無限デッキのブラックジャックでは、A2 vs. 5も同様にヒットするべきです。無限デッキの仮定は、ブラックジャックを分析する上で怠惰な方法です。私がこの方法を採用した理由は、このページはあまり利用されていないと考えたためであり、エラーによる損失は非常に小さく、202,000ユニットのベットにつき1ユニットのみだからです。
ブラックジャックでバックベットするプレイヤーとのスプリット戦略に誤りがあることに気づきました。バックベットする相手が10と8をスプリットする場合、片方のハンドだけをプレイする(これは利己的なチャートです)と書かれています。しかし、ハード10(ダブルなし)と8のスプリットは、依然としてプラスの期待値を持ちます。
理由は、私の表では、フロントプレイヤーが可能な限りリスプリットし続けると想定しているからです。フロントプレイヤーが同じミスを繰り返し続けると想定しているため、10が1枚あることの価値は下がります。その条件を該当ページに追加しただけです。
詳しいサイトをありがとうございます。ブラックジャックの付録9では、ゲーム全体の期待値と各プレイの期待値が示されています。ゲームの期待値はE i × P iの合計になると思います。ここで、E iはi番目のプレイ(スタンド/ヒット/ダブル/スプリット)の最大期待値、P i はi番目のプレイの確率です。この計算を試してみたところ、異なる結果になりました。例えば、6デッキ、ディーラーがソフト17でヒット、プレイヤーがスプリット後にダブルできないとすると、0.04518876になります。
これらのテーブルは、ディーラーがブラックジャックを持っていないことを前提としています。これは、プレイヤーの番が来る頃には、ディーラーはすでにブラックジャックを探しているからです。ダブルやスプリットの正しい判断は、ディーラーがブラックジャックを持っていないという条件付きの期待値に基づいて行うべきです。そうでなければ、プレイヤーは10やエースに対してダブルやスプリットをすることに過度に臆病になってしまうでしょう。確率と期待値のドット積を足し合わせると、ディーラーがブラックジャックの場合の損失は考慮されないため、誤った結果になります。
ゲーム全体のハウスエッジを求めるには、ディーラーがブラックジャックを持っている場合の期待損失を差し引く必要があります。6デッキの場合、ディーラーがブラックジャックになる確率は、10のカードの数×エースの枚数÷2枚のカードの組み合わせの数で、(6×16)×(6×4)/combin(312,2) = 0.047489となります。ただし、プレイヤーが負けるのは、自分がブラックジャックを持っていない時のみです。ディーラーが既にブラックジャックを持っている場合、プレイヤーがブラックジャックになる確率は、(6×16-1)×(6×4-1)/combin(310,2) = 0.045621となります。つまり、プレイヤーがディーラーのブラックジャックに負ける確率は、0.047489 × (1-0.045621) = 0.045323となります。この数値を上記のドット積から差し引くと、0.04518876 - 0.045323 = -0.00615144となります。したがって、付録に記載されているルールに基づくハウスエッジは0.62%となります。
私は 4 デッキ以上のブラックジャックの基本戦略に常に従おうとしていますが、ディーラーが 2、特に 3 に対して 12 をヒットすると、いつも嫌な顔をされます。他のプレイヤーに、自分がやっていることがなぜ最善なのか、簡単に説明する方法がわかりません。
気持ちは分かります。スペイン21では、3に対して14をヒットするといったプレーが求められるので、どれほどひどい状況になるか想像がつきます。見た目だけなら、大目に見ます。言葉に詰まったら、「他にもテーブルはたくさんありますよ」などと言うでしょう。オッズを説明しても、こんな単純な人間を説得できるはずがありません。馬鹿げた考えであればあるほど、執拗に信じてしまう傾向があるのです。
通常、あるプレイが他のプレイよりも優れている理由を簡潔に説明する方法はありません。正しいプレイがなぜそうなるのかを知るには、プレイヤーとディーラーの両方にとって、残りのカードがどうなるかあらゆる可能性を考慮するか、あるいは、非常にギリギリのハンドであれば何千回、何百万回とプレイしてみる必要があります。最も期待値の高い決定こそが、取るべき決定です。保険をかけないことだけが、簡単に説明できるものです。
表に書いてあることは理解しているのですが、ブラックジャックでディーラーが9、10、またはエースを持っている場合、8をスプリットする勇気が出ません。質問なのですが、これはハウスエッジにどのような影響を与えるのでしょうか?
6デッキ、ディーラーがソフト17でスタンド、プレイヤーが最大4ハンドまで再スプリットできると仮定しましょう。各基本戦略の変更の影響は、ハンドが発生する確率と、発生した際に正しいプレイを行わなかった場合のコストです。私のブラックジャック付録9には、各ハンドの確率と各プレイの期待値の両方が示されています。プレイヤーがスプリットではなくヒットを選択した場合、ゲームの期待値への影響は次のようになります。
確率(8,8 vs A)×(EV(ヒット)-EV(スプリット)) + 確率(8,8 vs 9)×(EV(ヒット)-EV(スプリット)) + 確率(8,8 vs 10)×(EV(ヒット)-EV(スプリット))
= 0.0003036 × (-0.513551 -(-0.364371)) + 0.0004404 × (-0.505707 -(-0.38995)) + 0.0016249 × (0.535361 -(-0.475385))
= -0.019%。
つまり、ディーラーが9、10、またはエースを持っているのに対して8、8をヒットすると、ハウスエッジは0.019%、つまり5,300ハンドに1ベット程度増加します。プレイヤーがヒットせずに降参した場合、その影響は0.013%に低下します。つまり、これは大きなミスではありません。比較すると、ディーラーがエースを持っているのに対してブラックジャックで「イーブンマネー」を取ると、6デッキゲームでハウスエッジは0.014%増加します。プレイヤーがブラックジャックと20(よくあるミス)にすべて保険をかけると、エラーコストは0.149%に跳ね上がります。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
少し前にストリップカジノで6-5のブラックジャックをプレイしていたのですが、無料のお酒を適量飲んでいたので、ディーラーが2-6の時にブラックジャックが出るたびに賭け金を倍にしていました。幸いにも毎回勝てました。でも、私の判断がどれほど間違っていたのか疑問に思います。ブラックジャックがイーブンマネーで支払われたら、意味があるのでしょうか?
私のブラックジャック付録9は、このような疑問に答えるのに役立ちます。例えば、6デッキでディーラーがソフト17を出した場合、ディーラーが5の場合にブラックジャックでダブルする期待値は0.622136、6の場合は0.667063です。どちらも1.2よりはるかに小さく、賭け金の半分以上を費やすことになります。残念ながら現在では時々起こるように、ブラックジャックがイーブンマネーしか支払わない場合でも、ブラックジャックではスタンドすべきです。ブラックジャックでスタンドすべきでない唯一のゲームはトリプルアップ21です。このゲームでは、ディーラーが6の場合にブラックジャックでトリプルベットすべきです。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
ブラックジャックの基本戦略表は、1ハンドあたりの期待値を最大化することに基づいています。しかし、ダブルやスプリットがヒットやスタンドに比べてわずかに悪いプレイであり、そのミスによる損失が追加のハンドをプレイすることによるハウスエッジよりも小さい状況はありますか?
はい!次の状況を考えてみましょう。
6デッキ
ディーラーがソフト17をヒット
プレイヤーはA,6を持っている
ディーラーは2を見せます
私のブラックジャック付録 9によると、各プレイの期待値は次のとおりです。
スタンド -0.152739
ヒット -0.000274
ダブル -0.004882
つまり、ヒットは、そのハンドで平均的に損失額が最も少ないプレイです。プレイヤーがダブルした場合、そのエラーの期待値は-0.004882 - (-0.000274) = -0.004608となります。私のブラックジャックハウスエッジ計算機によると、これらのルール(サレンダー、スプリット後のダブル、エースの再スプリットを想定)でのハウスエッジは0.48%です。通常、これらの選択肢の一部は許可されず、ハウスエッジが増加します。つまり、ディーラーが6デッキゲームでソフト17をヒットする限り、2に対してソフト17をダブルするコストは、追加のハンドに同額を賭けるコストよりも低くなります。
レイズが関わるゲームであれば、どんなゲームでも同じことが言えます。例えばスリーカードポーカーでは、1ハンドあたりの予想損失を最小限に抑えたい場合、最適な戦略はQ64以上のハンドでレイズすることです。これは私のスリーカードポーカーのページでも述べています。一方、ベット総額あたりの予想損失を最小限に抑えたい場合、最適な戦略はQ62以上のハンドでレイズすることです。
では、なぜ私のようなギャンブルライターは、賭け金総額ではなく、最初の賭け金あたりの期待損失を最小化することを戦略の基本とするのか、という疑問が湧いてきます。私の答えは、主に伝統によるものです。ブラックジャックの基本戦略はこのようにして生まれ、誰もが習慣と単純さからその手法を守り続けてきました。もしレクリエーショナルプレイヤーが一定期間の損失を最小限に抑えることを目標としているのであれば、1ハンドあたりの期待損失を最小限に抑える従来の戦略を採用すべきです。もしプレイヤーが合計$xを超える賭け金の損失を最小限に抑えることを目標としているのであれば、前述のような、やや悪いダブルやレイズを行うべきです。ほとんどのプレイヤーは時間ベースの目標を持ち、従来の戦略を好む傾向があると私は考えています。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
ブラックジャックのプレイヤーの多くは、9、10、またはエースに対して8をスプリットすることを好まないと知っています。このプレイは最も頻繁に間違えられるプレイだと思いますか?もしそうでないなら、何が間違いだと思いますか?
ブラックジャックのプレイヤーが最も間違える可能性が高いと思うプレイは、スプリット後のダブルが認められている状況で、5または6に対して4,4をスプリットすることです。6デッキゲームでどちらかの状況になる確率は1135分の1です。私のブラックジャック付録9によると、プレイヤーがスプリットではなくヒットすると仮定すると、期待値のコストは5に対して2.83%、6に対して4.38%です。全体として、プレイヤーがこのミスを習慣的に毎回犯すと、ゲームのハウスエッジは0.0032%上昇します。つまり、発生頻度が非常に低いため、それほど大きな損失をもたらすミスとは言えません。しかし、この状況で他のプレイヤーが正しくスプリットするのを見たことはありません。私が正しくスプリットするのを見たことがあるのですが、ディーラーや他のプレイヤーはたいてい呆れた顔をします。ある時、まるで私がそこにいないかのように、他のプレイヤーがディーラーに「Fで始まるハンドは絶対にスプリットしてはいけません」と間違って言うのを耳にしました。
もし、プレイ頻度とミスのコストの両方を考慮した上で、最もコストのかかるミスは何かと問われれば、推測することしかできません。その推測は、一番のミスは、ソフトダブルをすべき時に行わないこと、というものです。レクリエーショナルプレイヤーが、6に対してソフト17のようなハンドをダブルするのを目にすることは滅多にありません。次の表は、よくある4つのミスによるハウスエッジの増加を示しています。この表では、プレイヤーが状況発生時に常にミスを犯し、次善の策を取ることを前提としています。2または3に対して12でスタンドするケースについては、6、6のプレイヤーは含めていません。
ブラックジャックでよくある間違い
| エラー | 確率 | インシデントあたりの平均コスト | 1手あたりのコスト |
|---|---|---|---|
| 決してソフトダブル | 0.016430 | 0.054357 | 0.000893 |
| 2または3に対して12でスタンドする | 0.000380 | 0.029955 | 0.000380 |
| 9-Aに対してソフト18でスタンド | 0.000205 | 0.041605 | 0.000205 |
| 9-Aに対して8,8をヒット | 0.000194 | 0.081779 | 0.000194 |
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
なぜ基本戦略では10ではなく16でヒットするのに対し、ハイローカウントではカウントが0以上の場合はスタンドするのでしょうか?基本戦略はフルシュー、つまりカウントが0であることを前提としているのではないでしょうか?どちらも正しくないように思えます。
まず、16対10はヒットとスタンドの非常にギリギリのハンドであることを改めて強調しておきます。もしサレンダーが認められているなら、基本戦略プレイヤーにとってはヒットかスタンドするよりもはるかに有利です。そうでなければ、平均的にはヒットする方がわずかに有利です。8デッキのシューからスモールカードを1枚取り除くだけで、スタンドする確率が上がります。スモールカードが1枚減るとラージカードが多くなり、ヒットする方が危険になるからです。だからこそ、16が3枚以上のカードで構成されている場合はスタンドすべきだと私は言います。3枚の16は、通常シューから少なくとも2枚のスモールカードを取り除いているからです。
第二に、シャッフル後の最初のハンドにおいて、基本戦略とカードカウンティング戦略のプレイ方法が異なる場合、基本戦略が優先されます。基本戦略は、観察された特定のカードに基づいてデッキの構成を正確に考慮するように慎重に作成されています。インデックス値の表は、シュー全体に適用できるより鈍いツールです。
この特定のケースでは、カードカウンターは真のカウントをどのように切り捨てるかによってヒットするかスタンドするかを選択できます。切り捨てた場合、真のカウントは-1となり、ヒットとなります。切り上げた場合、つまり最も近い整数にした場合、真のカウントは0となり、スタンドとなります。ちなみに、ドン・シュレシンジャー著『ブラックジャック・アタック』によると、切り捨ての方法として「フロアリング」、つまりこの場合は-1に切り捨てる方法が選ばれており、プレイヤーは正しくヒットとなります。
もう一つの似たような状況は、15対10です。83%の確率で(10+5または8+7で、9+6ではない)、シャッフル後の最初のハンドでランニングカウントが-1になり、降伏のインデックス番号は0になります。切り捨てにより、降伏した方が良い場合でも、プレイヤーは誤ってヒットすることになります。
結論として、シャッフル後の最初の決定において、他のプレイヤーのカードがまだ分かっていない場合、カードカウンターは基本戦略を用いるべきです。その後は、インデックス番号の使用を再開します。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。


