確率 - サイコロ
標準的な 6 面サイコロを 6 個振った場合、同じ目が 6 つ出る確率はどれくらいでしょうか?
答えは 6*(1/6) 6 = 6/46,656 = 1/7,776 =~ 0.0001286 です。
シューターが「セブンアウト」するまでの平均ロール回数は? 7は6ロールに1回出ることは分かっていますが、カムアウトの7~11やクラップス、さらにシューターが複数ポイントを獲得する可能性を考えると、平均ロール回数は予想よりも多くなるかもしれません。これに関する数学的な参考資料はありますか?
シューター1人あたりの平均ロール回数は8.525510回です。2回から200回ロールする確率については、クラップスの生存確率のページをご覧ください。
サイコロ (クラップス/ドント パス ライン) を 100,000 回振ったとき、DP ベットで 2 回、3 回、4 回、5 回、6 回、7 回、8 回、または 9 回連続で負ける確率 (および頻度) はどれくらいでしょうか。
私のクラップスの付録では、あらゆる賭けのオッズを計算する方法を紹介しています。ドントパスベットで負ける確率は2928/5940であることがわかります。n回連続で負ける確率は(2928/5940) nです。10万回のうちn回負ける確率は、100,000 * (2928/5940) n+2とほぼ近似できます。
1 回のサイコロ投げで 6 個のサイコロを同じ数が出る確率はどれくらいでしょうか?
6個のサイコロで同じ数字が6つ出る確率は、6*(1/6) 6 =1/7776 =~ 0.01286% です。
サイコロを28回振って7が出ないというのは、どれくらいの頻度で起こりますか?どうやって計算するんですか?素晴らしいサイトですね、おめでとうございます。
お褒めいただきありがとうございます。2つのサイコロを28回振って7が出ない確率をおっしゃっているのだと思います。1回も7が出ない確率は5/6です。28回振って7が出ない確率は(5/6) 28 = 0.006066、つまり約165分の1です。
東洋のサイコロゲームについて質問です。プレイヤーはサイコロのどの面が出るかを推測します。まず、ルーレットのように1、2、3、4、5、6に賭け、次にディーラーが3つのサイコロを同時に振ります。配当は、選んだ数字が3つのサイコロのいずれかに1回出れば1:1、2回出れば2:1、3つのサイコロすべてに出れば3:1です。プレイヤーはボードに何度でも賭けることができますが、最適な賭け回数はいくつでしょうか?(賭け金がすべて同じ額だと仮定した場合)
3つ揃う確率は1/216です。2つ揃う確率は3*5/216です。1つ揃う確率は25*5/216です。0つ揃う確率は5*5*5/216です。したがって、期待リターンは3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7.87%となります。最適なベット回数というものはなく、どのような賭け方をしても、期待される総資金の7.87%を失うことになります。
これらの賭けはシックボーとチャック・ア・ラックの両方で行うことができます。
ウィザードさん、サイコロを 4 個振ったときにツーペアが出る確率はどれくらいですか?
ペアの組み合わせは、combin(6,2)=15通りあります。特定のツーペアが出るサイコロの出目は、 combin (4,2)=6通りあります。4つのサイコロを振る場合、6^4=1296通りあります。したがって、確率は90/1296=6.9444%です。
サイコロを1つ振ると、6が出る確率は1/6です。サイコロを2つ振ると、どちらか1つが6が出る確率は上がりますか、それとも1/6のままですか?
x個のサイコロを振った場合、少なくとも1つの6が出る確率は1-(5/6) 2です。サイコロを2個振った場合、この確率は30.56%です。
6 個のサイコロを使って 3 個の 1 を出す方法は何通りありますか?
まず、6個のサイコロの中から3個の1が出る確率は、(6,3)=20通りあります。残りの3個のサイコロはそれぞれ5つの数字のいずれかになります。つまり、合計は20×5 3 =2500通りです。すべてのサイコロを投げる確率は6 6 =46,656通りなので、ちょうど3個1が出る確率は2500/46656=0.0536です。combin関数の使い方については、ポーカーの確率のセクションをご覧ください。
3つのサイコロを同時に投げたとき、1つのサイコロが1の目を出す確率はどれくらいですか?私の理解では50%(1/6+1/6+1/6=1/2 -->50%)のはずですが、あなたのオッズ表では34.72%と表示されています。助けてください。
3 つのサイコロを振って 1 つだけ 1 が出る確率は、3*(5/6) 2 *(1/6) = 75/216 = 34.72% です。
4 つのサイコロを投げたときに「ペア」が出る確率はどれくらいでしょうか?
ペアは6つの数字のいずれかになります。残りの2つのシングルトンは、他の5つの数字のいずれかになります。したがって、6*combin(5,2)=60通りの組み合わせが既に存在します。ペアが出る可能性のあるサイコロの組み合わせは、combin(4,2)=6通りあります。2つのシングルトンは2通りの並び方が可能です。したがって、ペアが出る可能性は60*12=720通りあります。サイコロを投げる方法の総数は6 4 =1296通りです。したがって、確率は720/1296 =~55.56%となります。
友人がバーを経営していて、「本日のシェイク」というメニューがあります。タッパーウェアの容器にサイコロが10個入っています。1回のシェイクで10個中8個が出る確率はどれくらいでしょうか?お時間をいただきありがとうございました。
10個のサイコロを振って8個の目がすべて同じになる確率は、6*combin(10,8)*(1/6) 8 *(5/6) 2 = 1/8957.952です。少なくとも8個が同じになる確率は、6*[combin(10,8)*(1/6) 8 *(5/6) 2 + combin(10,9)*(1/6) 9 *(5/6) + (1/6) 10 ] = 1/8569.469です。
最近バックギャモンをしていて、ダブル6が4回連続で出ました。また同じことが起こる確率はどれくらいでしょうか?
新しいロールごとに、次の 4 回のロールがすべて 6 のダブル 6 になる確率は (1/36) 4 = 1679616 分の 1 です。
5 個のサイコロを 1 回投げてストレートが出る確率はどれくらいでしょうか?
スパンは1から5と2から6の2種類が考えられます。それぞれのスパンは5!=120通りの順序で並べることができます。5個のサイコロを振る方法は6× 5 =7776通りあります。したがって、確率は2×120/7776=3.09%です。ヤッツィーのゲーム中にラージストレートのマーク0をつけた直後は、この確率がかなり高くなるようです。
公平な面を持つサイコロを30回振った場合、1が出る期待回数はどれくらいですか?また、1が期待回数出る確率はどれくらいですか?
1 の予想される数は 30*(1/6) = 5 です。1 がちょうど 5 個ある確率は、combin(30,5)*(1/6) 5 *(5/6) 25 = 19.21% です。
任意の数のサイコロを振った場合、すべてを振ったときに少なくとも 1 つが 1 になる確率はどれくらいでしょうか。
全てのサイコロが1にならない確率は(5/6) nです。したがって、少なくとも1つ1が出る確率は1-(5/6) nです。例えば、サイコロを5個出すとします。答えは1-(5/6) 5 = 59.81%です。
36 個のサイコロを投げた場合、少なくとも 1 つの 6 が出る可能性はどれくらいでしょうか?
1-(5/6) 36 = 99.86%
サイコロを投げ続けて、そのたびに 6 をすべて取り除いた場合、特定の回数投げた後に残っているサイコロの理論的な数をどのように予測するのでしょうか。
1回振るごとに、5/6個のサイコロが残ると期待されます。つまり、n回振った後に残るサイコロの期待値は36*(5/6) nとなります。例えば、10回振った場合、平均して5.81個のサイコロが残ります。
サイコロを 3 つ振ったとき、少なくとも 2 つの数字が同じになる確率はどれくらいでしょうか?
すべての数字が異なる確率は(5/6)*(4/6)=20/36です。したがって、少なくとも2つの数字が同じになる確率は1-(20/36)=16/36=44.44%です。
二人でサイコロを一つずつ振ったとき、同じ目が出る確率はどれくらいでしょうか?この答えを求める公式はありますか?
はい。2から12までの合計を計算してみて、それぞれを2回ずつ出す確率を求めるだけです。つまり、答えは(1/36) 2 +(2/36) 2 +(3/36) 2 +(4/36) 2 +(5/36) 2 +(6/36) 2 +(5/36) 2 +(4/36) 2 +(3/36) 2 +(2/36) 2 +(1/36) 2 = 11.27%となります。
先日、病院の祝賀会に参加しました。7つのサイコロを振って7回6が出たら賞品として新車がもらえるというものでした。1回1ポンド。これってきっと高い確率だと思うんですが、どれくらい高いんでしょうか?
7個のサイコロで7つの6が出る確率は(1/6) 7 = 279,936分の1です。つまり、この賭けが良い結果になるには、車の価値が279,936ポンド以上である必要があります。平均的なロールスロイスでさえこれほどの価値はありませんので、これはひどい賭けだったと言えるでしょう。
[ブルージェイが付け加える: ああ、そうだね。でも、チャリティーのためだったってことがポイントだったと思う。1ポンドをチャリティーに寄付して、何も返ってこないけど役に立ったって思える気持ちになるのと、1ポンドを寄付して気持ちいい気持ちに加えて、ひょっとしたら車が当たるかもしれないって思うのと、どっちが楽しい?]
5 個のサイコロを振ったとき、5 種類、4 種類、3 種類、フルハウス、2 ペア、ペア、ストレート、何も出ない確率はどれくらいでしょうか。
- 5枚の同じカード:6/6 5 = 0.08%(明らか)
- フォーオブアカインド: 5*6*5 = 1.93% (シングルトンの可能な位置 5 つ * フォーオブアカインドのランク 6 つ * シングルトンのランク 5 つ)。
- フルハウス: combin(5,3)*6*5/6 5 = 3.86% (スリーオブアカインドのcombin(5,3)の位置 * スリーオブアカインドの6ランク * ペアの2ランク)。
- スリー・オブ・ア・カインド: COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15.43%。(スリー・オブ・ア・カインドの位置 combin(5,3) * シングルトンのうち大きい方の位置 combin(2,1) * スリー・オブ・ア・カインド 6 ランク * 2 つのシングルトンのランク combin(5,2)。
- ツーペア: COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23.15% (上位ペアの combin(5,2) の位置 * 下位ペアの combin(3,2) の位置 * ツーペアの combin(6,4) のランク * シングルトンの 4 ランク。
- ペア: COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46.30% (ペアのcombin(5,2)の位置 * 3つのシングルトンのfact(3)の位置 * ペアの6つの順位 * シングルトンのcombin(5,3)の順位。
- ストレート: 2*fact(5) / 6 5 = 3.09% (ストレートの場合、{1-5 または 2-6} * fact(5) の順序を並べる方法は 2 スパンの場合があります)。
- なし: ((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6.17% (6 つのランクのうち 5 つを選択する方法は、ストレートの場合は 2 つを差し引いた、* 順序を並べ替える方法は fact(5) 通り。
ウィザードさん、こんにちは。この質問にお答えいただけると嬉しいです。17世紀フランスで人気のあったギャンブルゲームで、プレイヤーは2つのサイコロを24回振ります。そのうち少なくとも1回が6のダブルが出れば勝ちとなります。当時、勝率が50%を超えるか下回るかで議論がありました。何かお力添えいただけますか?
確かに、これは簡単です。24回投げて少なくとも1回12が出る確率は、1-(35/36) 24 = 49.14%です。つまり、12が出ない方に賭ける方が有利です。24回投げて12が出る期待値は2/3なので、これは賢い賭けと言えるでしょう。しかし、これは12が出る確率が2/3であることを意味するわけではありません。12が複数出る場合もあり、12に賭けたプレイヤーは最初の12が出た後、それ以上12が出ても勝てないからです。ある試行で勝つ確率をp、試行回数をn、少なくとも1回勝つ確率をwとすると、nをpとwで解くと…
w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n*log(1-p)
n=log(1-w)/log(1-p)
つまり、あなたの例では、n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051 となります。つまり、24.6回投げた場合の成功確率が50%であれば、24回投げた場合はわずかに低くなるはずです。
6 個のサイコロを振って 1、2、3、4、5、6 が 6 回連続で出る確率はどれくらいでしょうか?
6個のサイコロを1回振って123456が出る確率は、確率(2番目のサイコロが1番目のサイコロと一致しない) * 確率(3番目のサイコロが1番目または2番目のサイコロと一致しない) * ... = 1 * (5/6) * (4/6) * (3/6) * (2/6) * (1/6) = 0.015432 と表すことができます。つまり、これを6回連続で出す確率は 0.015432 × 6 = 74,037,208,411 分の 1 です。
サイコロを 6 回振ったとき、ちょうど 4 回「2」が出る確率はどれくらいでしょうか。
(6,2)*(1/6) 4 *(5/6) 2を合計すると 0.008037551 になります。
サイコロを 3 個、4 個、5 個振ったときに、出た目のうち最も高い 3 個を残しておける場合、13 以上が出る確率はどれくらいでしょうか。
確率は次のとおりです。
3つのサイコロ:25.93%
4つのサイコロ:48.77%
サイコロ5個: 66.13%。
6面サイコロを3つ振るとします。3つの目の合計が12である場合、最初のサイコロの目が4になる条件付き確率はいくらでしょうか?
AがBの場合の確率は、AとBの確率をBの確率で割ったものです。この場合、最初のサイコロで4が出た後、残りの2つのサイコロの合計が8になる確率は(1/6)*(5/36) = 5/216です。私のシックボーのセクションで示したように、3つのサイコロで合計が12になる確率は25/216です。したがって、答えは(5/216)/(25/216) = 5/25 = 20%となります。
最近のプログラミング演習で、私と他の学生は 6 面サイコロをコードで記述し、サイコロを使って簡単なゲームをプレイするように言われました。ゲームの目的は、サイコロを投げて、出た目の合計がちょうど 100 になるまで続けることです。100 を超えた出目は集計されず、単に統計情報に追加されます。すぐに、100 に達するのに必要な最小の投げ回数は 17 回であることが分かりました。しかし、その回数が発生する確率を計算するのは困難です。特定の順序でサイコロを投げる確率を計算するのは比較的簡単ですが、特定の順序で投げる場合と、17 回投げて 100 に達するさまざまな方法 (16*6 + 1*4 と 15*6 + 2*5) の両方をどのように考慮すればよいのでしょうか。
あなたが挙げた2つの方法は、17回投げて合計100を出す唯一の方法です。6が16回出て4が1回出る確率は17*(1/6) 17です。4の出る順番は17通りあり、それぞれの順番の確率は(1/6)*(1/6)*...*(1/6)で、17項で表されます。6が15回出て5が2回出る確率は(17,2) = 136通りです。つまり、6が15回出て5が2回出る確率は136*(1/6) 17です。つまり、合計確率は(17+136)*(1/6) 17 = 110,631,761,077分の1です。
サイコロが3つあります。2つは6面体のサイコロで、1つはすべての面に6があるサイコロです。サイコロはすべてポケットの中にあります。ランダムにサイコロを1つ取り出して投げます。結果は6でした。そのサイコロが6つの異なる目を持つサイコロの1つである確率はどれくらいでしょうか?
A = 通常のサイコロを選択する
B = ランダムに選んだサイコロで6が出る
答え = Pr(A given B) = Pr(A and B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4。
6 個のサイコロを 1 回だけ振ることができる場合、6、6、6、6、1、4 がどの順序でも出る確率はどれくらいでしょうか。
これらの数字を任意の順序で並べると、6!/(4!*1!*1!) = 30通りあります。別の見方をすると、1を置く位置は6つ、4を置く位置は5つ残っているので、6*5=30となります。666614をまさにその順序で並べる確率は、6の6乗分の1 = 46656分の1です。これを30倍して30通りの順序を考えると、答えは30/46656 = 0.0643%、つまり1552.2分の1となります。
ある事象の「待ち時間」とは、その事象の確率の逆数だと私は理解しています。1つのサイコロを使って2が連続して出るまでの待ち時間を計算したいと考えています。シミュレーションでは平均42回出ます。この待ち時間を、2が連続して出る確率とどのように関連付ければよいでしょうか?
単一の事象において、確率がpであれば平均待ち時間は1/pであることは事実です。しかし、連続する事象の場合は状況はより複雑になります。xを、最後のロールが2でなかった状態とします。これは開始時の状態でもあります。yを、最後のロールが2だった状態とします。最初のロールの後、状態xに留まる確率は5/6、状態yに留まる確率は1/6です。Ex(x)を状態xからのロールの期待値、Ex(y)を状態yからのロールの期待値とします。すると…
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y)、そして
Ex(y) = 1 + (5/6)*ex(x)
これら 2 つの方程式を解くと...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
例(x) = 36*(7/6) = 42
したがって、2 回連続して 2 が出る場合の平均待ち時間は 42 回です。
私も同じタイプの問題を抱えています。2 回表が出ると予想される回転数だけです。私の数学の問題のサイトで、問題 128 を参照してください。
サイコロを2個、3個、4個振った場合、同じ目が2つ出る確率はそれぞれどれくらいですか? サイコロを振る人が有利になるには、一度に何個のサイコロを振ればいいのでしょうか? (どの数字が2倍になるかは関係ありません。)
ロールの回数に応じて、少なくとも 1 つの数字が複数回出る確率は次のとおりです。
ペア以上の確率
| ロール | 確率 |
| 2ロール | 16.67% |
| 3ロール | 44.44% |
| 4ロール | 72.22% |
| 5ロール | 90.74% |
| 6ロール | 98.46% |
サイコロを20個振ったとき、合計が100を超える確率はどれくらいでしょうか?よろしくお願いします。
これを解くために正規近似法を使い始めましたが、100点を超える確率が低すぎるため、この方法は正確とは言えませんでした。そこで、825万回のランダムシミュレーションを行ったところ、101点以上の試行回数は127回でした。つまり、確率は約65,000分の1です。
ウィザードさん、カリフォルニア・スーパーロト・プラス(4140万分の1)の当選確率を、7または11が連続して出る回数で説明していただけますか?どこかで聞いたことがあります。ほとんどの人は宝くじの当選確率を理解できません。でも、サイコロを振る確率なら、誰でも理解できるはずです。
答えをnとします。7か11が出る確率は8/36です。nを求めるには、次のようにします。
(8/36) n = 1/41,400,000
log((8/36) n ) = log(1/41,400,000)
n × log(8/36) = log(1/41,400,000)
n = log(1/41,400,000)/log(8/36)
n = -7.617 / -0.65321
n = 11.6608
つまり、スーパーロトに当たる確率は、7または11を11.66回連続で投げるのと同じです。部分的な投げの意味がわからない人のために言い換えると、確率は11回から12回連続で投げた場合の間になります。
従業員間で意見の相違があります。通りの向こうに、1日1回シェイクを提供しているバーがあります。これは、一度に5つのサイコロを投げて、全て同じ目が出なければならないというものです。「ヤッツィーのように」ですが、3回チャンスが与えられます。ただし、3回とも全てのサイコロを拾わなければなりません。そこで質問なのですが、1回のシェイクで同じ結果になる確率と、3回のシェイクで同じ結果になる確率はそれぞれどれくらいでしょうか。もし既に回答されていたら申し訳ありませんが、見つけることができませんでした。
1回の投げで5種類の目が出る確率は、6*(1/6) 5 = 1/1,296です。これは、5種類の目(1から6まで)が6種類あり、各サイコロでその目が出る確率が(1/6)だからです。5種類の目が出ない確率は、1-(1/1,296)=1,295/1,296です。3回投げても3種類の目が出ない確率は、(1,295/1,296) 3 =99.77%です。つまり、3回投げて少なくとも1つの5種類の目が出る確率は、100%-99.77% = 0.23%です。
偏りのない 6 面サイコロで、それぞれの可能な結果のうち少なくとも 1 つを得るために必要なサイコロを投げる回数の予想値はいくつですか。
何かの確率がpだとすると、平均して最初にそれが起こるまでには1/p回の試行が必要です。当然、最初のサイコロ投げでは1つの数字を消します。次に他の5つの数字のいずれかが出る確率は5/6です。つまり、それが起こるまでには平均して1/(5/6)=6/5=1.2回のサイコロ投げが必要になります。この推論を最後まで当てはめると、期待されるサイコロの回数は(6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1)=14.7となります。
5 個のサイコロを振って合計が 12 になる一般的な確率はどれくらいでしょうか。
1個から25個のサイコロを使った場合の、このような質問に答える新しいセクションを追加しました。よろしければご覧ください。5個のサイコロを使った表に示されているように、合計が12になる確率は0.039223251028807です。
2 つのサイコロを繰り返し振って、次のいずれかのイベントが発生した場合、どちらが先に発生する可能性が高いでしょうか。
- 合計で 6 と 8 が出た場合、順序は問わず、重複も許可されます。
- 合計7が2回出ます。
誰かが私に、6と8が最初に出るという賭けを持ちかけてきました。7が一番可能性が高いので、賭けに応じました。しかし、これを何度も繰り返して2,500ドルを失いました。オッズはどれくらいでしょうか?
残念ながら、この賭けはスクエア側でしたね。6と8が出る前に7が2つ出る確率は45.44%です。これがすべての可能性のある結果です。最初の列は、賭けの結果に対する意図的なロールの順序で、他のすべての列は無視されます。
2つの7と6と8の賭けの前に
| 関連ロール | 確率 | 式 | 結果 |
| 6,8 | 0.142045 | (5/16)*(5/11) | 失う |
| 8,6 | 0.142045 | (5/16)*(5/11) | 失う |
| 6,7,8 | 0.077479 | (5/16)*(6/11)*(5/11) | 失う |
| 7,6,8 | 0.053267 | (6/16)*(5/16)*(5/11) | 失う |
| 8,7,6 | 0.077479 | (5/16)*(6/11)*(5/11) | 失う |
| 7,8,6 | 0.053267 | (6/16)*(5/16)*(5/11) | 失う |
| 7,7 | 0.140625 | (6/16)*(6/16) | 勝つ |
| 6,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | 勝つ |
| 8,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | 勝つ |
| 7,6,7 | 0.06392 | (6/16)*(5/16)*(6/11) | 勝つ |
| 7,8,7 | 0.06392 | (6/16)*(5/16)*(6/11) | 勝つ |
基本的に、6 と 8 がより良い側である理由は、これらの数字を 6、8、または 8、6 のどちらの順序でも当てることができるからです。7 が 2 つある場合は、7、次にもう 1 つの 7 という 1 つの順序しかありません。
2つ質問があります。1) 6面サイコロを6個振って、一度に6、6、6、6、6、6が出る確率はどれくらいですか? 2) 6面サイコロを6個振って、一度に1、2、3、4、5、6が出る確率はどれくらいですか? ありがとうございます!もう困っています!
6つの6が出る確率は(1/6) 6 = 46656分の1です。6つのサイコロを振って1、2、3、4、5、6が出る確率は6 ! /6 6 = 64.8分の1です。
サイコロを 10 回振ったとき、特定の数字が複数回出る確率はどれくらいでしょうか。
1-(5/6) 10 -10 × (1/6) × (5/6) 9 = 51.55%.
「課税と脱税」というゲームで、プレイヤーはサイコロを2つ振ります。出た目の合計が7、11、または12であれば、プレイヤーは税務調査を受けます。それ以外の出目が出れば、プレイヤーは税金を逃れることができます。プレイヤーがサイコロを5回振った場合、税金を逃れられる確率はどれくらいでしょうか?
7、11、または12が出る確率は(6+2+1)/36 = 9/36 = 1/4です。この数字の導き方については、サイコロの確率の基礎に関するセクションをご覧ください。それ以外の目が出る確率は3/4です。5回サイコロを振って7、11、または12が出ない確率は(3/4) 5 = 23.73%です。
サイコロを何回振れば、1、2、3、4、5、6の目がそれぞれ少なくとも1回は出る可能性が高くなりますか?これをn面サイコロに一般化する方法について何かアイデアはありますか?
質問されたわけではないのですが、まずは平均値についてお話ししましょう。6面サイコロの場合、各面が少なくとも1回出る期待値は(6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14.7です。n面サイコロの場合、期待値は(n/n) + (n/(n-1)) + (n/(n-2)) + ... + nです。必要なサイコロの回数の中央値は13です。13回以下になる確率は51.4%、13回以上になる確率は56.21%です。
ダイスのコントロールに懐疑的なのは承知しています。ダイスのセッティングとコントロールされた射撃を3ヶ月間練習してきました。ランダムに655回投げて、7が78回出る確率はどれくらいでしょうか? 助言ありがとうございます :)
投げる回数が多い場合は、ガウス曲線近似を使用できます。655回投げた場合の7の期待値は、655 × (1/6) = 109.1667です。分散は655 × (1/6) × (5/6) = 90.9722です。標準偏差はsqr(90.9722) = 9.5379です。78個の7は、期待値より109.1667 − 78 = 31.1667少なくなります。これは、(31.1667 - 0.5)/9.5379 = 3.22標準偏差分、期待値より低い値です。期待値より3.22標準偏差以上低い値になる確率は0.000641、つまり1,560分の1です。この数値は、Excel で normsdist(-3.22) という式を使用して取得しました。
これはクラップスにおけるサイコロのコントロールについてです。以前、スタンフォード・ウォンの実験について議論し、「賭けの条件は、精密シューターがサイコロを500回振って7の出目を79.5回未満にできるかどうかでした。ランダムなゲームでの期待値は83.33です。ランダムに500回振って79回以下の7が出る確率は32.66%です。ランダムに500回振って74回以下の7が出る確率は14.41%です。」と述べていました。
この賭けに関して私が疑問に思っているのは、14.41% では依然として「統計的に有意」ではない (つまり p < 0.05) ということです。これは通常、平均値からの標準偏差が 2 より大きい、つまり、一連のどちらかの時点でイベントがランダムに発生する確率が *合計* 5% 未満であることを意味します。
結果が完全にランダムである(つまり、結果が統計的に有意である)可能性が 2.5% 未満であると言えるには、500 回のロールで 7 が何回出なければならないでしょうか。
本当にありがとうございます。ところで、あなたのサイトは、ギャンブルのオッズと確率に関して私が見つけたサイトの中で間違いなく最高のサイトです。これからも頑張ってください。
親切なお言葉をありがとうございます。「ランダムでない結果が出る確率はp」と書くべきではありません。正しくは「ランダムなゲームでそのような結果が出る確率はp」と書くべきです。500回のサイコロ投げで何かを証明したり反証したりするとは誰も思っていませんでした。79.5の7というラインを設定したのも私ではありませんが、統計的に有意になるように設定したとは思えません。むしろ、両者が賭けに同意するポイントだったのではないかと思います。
2.5%の有意水準は、期待値からの標準偏差1.96倍です。これはExcelの式 =normsinv(0.025) で求められます。500回投げた場合の標準偏差は、sqr(500*(1/6)*(5/6)) = 8.333です。つまり、標準偏差1.96倍ということは、期待値より1.96 * 8.333 = 16.333倍低いことになります。500回投げた場合の7の期待値は、500*(1/6) = 83.333です。つまり、標準偏差1.96倍低いということは、83.333 - 16.333 = 67倍です。二項分布を用いて検証すると、7が67個以下になる確率は正確には2.627%です。
ヤッツィーを獲得するために必要な予想ロール回数はどれくらいですか?
プレイヤーが常に最も多く出現する数字を持っていると仮定すると、平均は11.09になります。以下は、8260万回のランダムシミュレーションにおけるロール回数の分布を示す表です。
ヤッツィー実験
| ロール | 発生事例 | 確率 |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0.00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0.00392347 |
| 29 | 271321 | 0.00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0。00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| 合計 | 82600000 | 1 |
サイコロを振ってゲームをする仮想的なゲームを考えてみましょう。サイコロが1を出した場合、プレイヤーは1ドルを失い、ゲームは終了します。それ以外の目が出た場合、プレイヤーは1ドルを獲得します。この時点で、プレイヤーはそのままゲームを続けるか、ゲームを放棄するかを選択できます。プレイヤーは負けるかゲームを放棄するまで、賭け金を倍にしてゲームを続けることができます。最善の戦略は何でしょうか?
期待値を最大化するという観点だけで言えば、プレイヤーは永遠にプレイし続けるべきです。プレイヤーが最終的に負ける確率は1ですが、どの決定点においても、期待値は常にもう一度プレイする方に有利です。一見矛盾しているように見えますが、その答えは、確率が1であっても、実際には起こらない可能性があるという事実にあります。例えば、0から10までの数直線にダーツを投げた場合、円周率にぴったり当たらない確率は1ですが、それでも起こり得ます。
しかし、現実的には、ある程度の限界があります。それは、お金がもたらす幸福度は金額に比例しないからです。お金が増えれば増えるほど幸福度も増すというのは一般的に認められていますが、お金が増えれば増えるほど、1ドルごとに得られる幸福度は少なくなるのです。
この質問に答える良い方法は、ケリー基準をこの問題に適用することだと私は考えています。ケリー基準によれば、プレイヤーは賭け金が総資産の96.5948%を超えるまで、あらゆる決定を下すべきです。つまり、(私は多くの計算を省略しました)プレイヤーは賭け金が総資産の96.5948%を超えるまで賭け金を倍増し続けるべきです。資産とは、勝ち金とプレイヤーが最初の賭けを行う前に持っていたお金の合計と定義されます。例えば、プレイヤーが最初に10万ドルを持っていたとしたら、23回賭け金を倍増させ、4,194,304ドルを獲得するまで賭け続けるべきです。その時点で、プレイヤーの総資産は4,294,304ドルになります。彼は総資産の 4,194,304/4,294,304 = 96.67% を賭けるよう求められますが、これは 96.5948% の停止ポイントより大きいため、やめる必要があります。
プレイヤーAとBはサイコロを2つ振ります。プレイヤーAがBより先に合計6が出れば勝ち、BがAより先に合計7が出れば勝ちです。Aが先に6が出れば勝ちです。Aが先攻の場合、Aが勝つ確率は30/61であることを示してください。
この問いの答えをpとしましょう。合計が6になる確率は5/36、合計が7になる確率は6/36です。なぜそうなるのか理解できない場合は、サイコロの確率の基礎に関するセクションを参照してください。pは次のように定義できます。
p = 確率(最初のロールで 6 が出る) + 確率(最初のロールで 6 が出ない)*確率(2 番目のロールで 7 が出ない)*p。
これは、最初の 2 回のロール後にどちらのプレイヤーも勝てなかった場合、ゲームは元の状態に戻り、プレイヤー A が勝つ確率は同じままであるためです。
つまり、次のようになります。
p = (5/36) + (31/36)×(30/36)×p
p = 5/36 + (930/1296)×p
p * (1-(930/1296)) = 5/36。
p * (366/1296) = 5/36
p = (5/36)×(1296/366) = 30/61。
6面の、異なる目を持つサイコロをn個振る場合、何通りの出目がありますか? 前述の通り、サイコロは異なる目を持つので、例えば5個のサイコロで1-1-3-5-6と1-6-5-1-3の出目は同じ目とみなされます。サイコロが2個の場合は、答えが21であることは容易に分かりますが、簡潔で一般的な解法が思いつきません。
答えはcombin(n+5,n) = (n+5)!/(120×n!)と表すことができます。1個から20個のサイコロの場合の答えは次のとおりです。
区別できないサイコロの組み合わせ
| サイコロ | 組み合わせ |
| 1 | 6 |
| 2 | 21 |
| 3 | 56 |
| 4 | 126 |
| 5 | 252 |
| 6 | 462 |
| 7 | 792 |
| 8 | 1287 |
| 9 | 2002 |
| 10 | 3003 |
| 11 | 4368 |
| 12 | 6188 |
| 13 | 8568 |
| 14 | 11628 |
| 15 | 15504 |
| 16 | 20349 |
| 17 | 26334 |
| 18 | 33649 |
| 19 | 42504 |
| 20 | 53130 |
| 21 | 65780 |
| 22 | 80730 |
| 23 | 98280 |
『Applied Combinatorics 』の著者、Alan Tucker 氏に感謝します。
サイコロを振ったとき、2つの数字が連続して出る確率を計算できますか?つまり、4が2つ、6が2つ、7が2つ連続して出る確率はどれくらいですか?過去が未来を予測することはできないことは承知していますが、7/36 × 7/36 が連続して出る確率を計算する方法はあるでしょうか?意味が通じるといいのですが。
はい。Pr(2) 2 + Pr(3) 2 + ... + Pr(12) 2 = (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (2/36) 2 + (1/36) 2 = 11.27%となります。
サイコロを 180 回連続で振った場合、次の結果が出る回数は何回ですか。
7が2つ連続ですか?
7が3つ連続ですか?
7が4回連続ですか?
お時間をいただきありがとうございます:-)。
この情報を知る有益な理由は思いつきませんが、この種の質問はよく受けるので、お答えします。
最初のサイコロから始めて、または最後のサイコロで終わる特定の7の連続を出すのは、その連続が片側で有界であるため、少し簡単です。具体的には、最初のサイコロから始めて、または最後のサイコロで終わるs個の7の連続を出す確率は、(1/6) s ×(5/6)です。5/6という項は、連続の端で7以外の目が出なければならないためです。
連続する7が連続する確率は、途中のどの時点でも(1/6) s × (5/6) 2 です。プレイヤーは連続する両端で7以外の数字を必ず出さなければならないため、5/6の項を2乗します。
r回のロールの場合、内側の連続が2箇所、n個の7が連続する箇所がrn-1箇所あります。これらの式を表にまとめると、1から10までの7の連続の期待値は以下のようになります。「内側」の列は2*(5/6)*(1/6) r 、「外側」の列は(179-r)*(5/6) 2 *(1/6) rです。ここで、rは連続する7の数です。つまり、7が2個連続する確率は3.46回、7が3個連続する確率は0.57回、7が4個連続する確率は0.10回と予想されます。
180回のロールで7が連続する予想回数
| 走る | 内部 | 外 | 合計 |
| 1 | 0.277778 | 20.601852 | 20.87963 |
| 2 | 0.046296 | 3.414352 | 3.460648 |
| 3 | 0.007716 | 0.565844 | 0.57356 |
| 4 | 0.001286 | 0.093771 | 0.095057 |
| 5 | 0.000214 | 0.015539 | 0.015754 |
| 6 | 0.000036 | 0.002575 | 0.002611 |
| 7 | 0.000006 | 0.000427 | 0.000433 |
| 8 | 0.000001 | 0.000071 | 0.000072 |
| 9 | 0 | 0.000012 | 0.000012 |
| 10 | 0 | 0.000002 | 0.000002 |
2 つのサイコロを振って、合計が 12 になるか、2 回連続して合計が 7 になるまで続けます。最初に 12 が出る確率はどれくらいでしょうか。
答えと解答は、私の関連サイトmathproblems.infoの問題 201 にあります。
私はテーブルゲームをするのですが、友人と非立方体プラトン立体サイコロ(もしあなたが相当なオタクなら、d4、d8、d12、d20のことを指します)について議論していました。彼らは、それらが唯一、実証的に公平なサイコロだと主張しました。私は、それらを公平に製造するのはあまりにも困難すぎると主張しました。それに、ゲームはクラップスの亜種くらいしかできないでしょうが、追加の結果の数が多いため、非常に扱いにくくなってしまいます。カジノで、非伝統的な6面サイコロを使ったゲームがあったことはありますか?
|
正多角形に限定し、すべての面の確率を等しくしたい場合、プラトン立体に限定されます。しかし、正多角形という条件を緩和できれば、13個のカタラン立体も追加できます。
もう一つの質問にお答えすると、いいえ、カジノでサイコロ以外のサイコロを使ったゲームを見たことはありません。10年ほど前、アトランティックシティのゲームショーで、カタルーニャ立体の一つである菱形三十面体を使ったゲームのデモを見たことがありますが、カジノで実際にプレイされたことはなかったと思います。毎年グローバル・ゲーミング・エキスポで見かけるゲームで、回転するコマ(ドレイドルのような)を使ったものがありますが、残念ながら、カジノで見たことがありません。
6 面サイコロを 3 つ振った場合、ストレートが出る確率はどれくらいでしょうか。また、スリー・オブ・カインドが出る確率はどれくらいでしょうか。
3つのサイコロを振る方法は6⁻⁻ =216通りあります。そのうち6通りの組み合わせはスリーカード(1-1-1から6-6-6)になります。したがって、スリーカードが出る確率は6/216 = 1/36です。ストレートが出る可能性のある組み合わせは4通り(1-2-3から4-5-6)あります。また、3つのサイコロをストレートに並べる方法は3!=6通りあります。つまり、ストレートの組み合わせは4*6=24通りあります。したがって、ストレートが出る確率は24/216 = 1/9です。
6面サイコロを4つ振って、最も低い目を引いた後の平均値(4d6-L)はいくらですか?このサイコロの標準偏差はいくらですか?
次の表は、3 から 18 までのすべての可能な合計の組み合わせの数を示しています。
4d6-Lの組み合わせ
| 結果 | 組み合わせ |
| 3 | 1 |
| 4 | 4 |
| 5 | 10 |
| 6 | 21 |
| 7 | 38 |
| 8 | 62 |
| 9 | 91 |
| 10 | 122 |
| 11 | 148 |
| 12 | 167 |
| 13 | 172 |
| 14 | 160 |
| 15 | 131 |
| 16 | 94 |
| 17 | 54 |
| 18 | 21 |
| 合計 | 1296 |
平均結果は 12.2446、標準偏差は 2.8468 です。
サイコロの確率について質問です。7が出る確率は6通り、12が出る確率は1通りあることは知っていますが、7が6つ出た後12が1つ出る確率はどれくらいでしょうか? 偶数ですか? 偶数でない場合、偶数にするには12をいくつ加えればよいでしょうか?
7が出る確率は1/6、12が出る確率は1/36です。7か12が出た場合、7が出る確率は(1/6)/((1/6)+(1/36)) = 6/7です。つまり、6か12が出た場合、最初の6回で毎回6が出る確率は(6/7) 6 = 39.66%です。
質問を「12が出る前に6が5つ出る確率は?」と言い換えると、答えは(6/7) 5 = 46.27%です。4つ出る場合は(6/7) 4 = 53.98%です。つまり、12が出る前に7が出る確率が50/50になるような数字は存在しません。もしあなたが良い賭けを探しているなら、12が出る前に7が4つ出るか、7が5つ出る前に12が出るかのどちらかを提案しましょう。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
6面サイコロをd個振って合計tが出る確率を計算する簡単な方法はありますか?
英国サマセットのロバート・グッドハンド氏による便利な裏技をご紹介します。まず、次のように、6つの1とその両側に5つの0を並べます。
1つのサイコロの確率
| サイコロの合計 | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||
| 1つのダイ | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
これは、1つのサイコロで1から6の目が出る組み合わせの数を表しています。当たり前ですよね。でも、もう少しだけお付き合いください。サイコロが2つの場合は、一番下にもう1行追加し、各セルについて、上の行とその左側の5つのセルの合計を求めます。さらに計算を続けたい場合は、右側にダミーの0を5つ追加します。これは、合計が2から12になる組み合わせを表しています。
2つのサイコロの確率
| サイコロの合計 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||||||||
| 1つのダイ | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2つのサイコロ | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
サイコロが3つの場合は、これを繰り返します。これは3から18までの組み合わせの数を表します。
任意の合計の確率を求めるには、その合計の組み合わせの数を、組み合わせの総数で割ります。サイコロを3つ振る場合、合計は216で、これも6÷ 3と簡単に求められます。例えば、サイコロを3つ振って合計が13になる確率は、21÷216 = 9.72%です。
つまり、d個のサイコロの場合は、1個からd-1個まで順番に計算していく必要があります。これはどのスプレッドシートでも簡単に行えます。
少なくとも 1 つの 12 が出る確率が 50/50 になるには、2 つのサイコロを何回振る必要がありますか。
これは確率論の歴史における古典的な問題です。多くの人が答えは18だと誤解しています。なぜなら、12が出る確率は36分の1で、18×(1/36)=50%だからです。しかし、その論理では、36回振って12が出る確率は100%になりますが、明らかにそうではありません。正しい解は次のとおりです。rを振る回数とします。1回振っても12が出ない確率は35/36です。r回振って12が0個ある確率は(35/36) rです。したがって、次の式でrについて解く必要があります。
(35/36) r = 0.5
log(35/36) r = log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051
つまり、丸められた答えはありません。24回振って12が出る確率は1-(35/36) 24 = 49.14%です。25回振って12が出る確率は1-(35/36) 25 = 50.55%です。
これに賭けるなら、例えば25回投げて12が出せるか、誰かが24回投げて12が出せないか、どちらにしても、イーブンマネーで有利になります。
このゲームを知らない方のために説明すると、攻撃側と防御側はそれぞれ1~8個のサイコロを振り、その時点でのそれぞれの軍隊数に応じて出目が大きくなります。出た目が大きい方が勝利します。同点の場合は防御側が勝利します。攻撃側が敗北した場合、攻撃を開始した領土に軍隊を1つ保持できます。そのため、攻撃には少なくとも2つの軍隊が必要です。攻撃に勝利した場合、1つは征服した領土に駐留し、もう1つは残留することができます。
次の表は、合計 64 通りのサイコロの組み合わせに応じて、攻撃側の勝利の確率を示しています。
攻撃側の勝利確率
| アタッカー | ディフェンダー | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 陸軍 | 2つの軍隊 | 3つの軍隊 | 4つの軍隊 | 5つの軍隊 | 6つの軍隊 | 7つの軍隊 | 8つの軍隊 | |
| 2 | 0.837963 | 0.443673 | 0.152006 | 0.035880 | 0.006105 | 0.000766 | 0.000071 | 0.000005 |
| 3 | 0.972994 | 0.778549 | 0.453575 | 0.191701 | 0.060713 | 0.014879 | 0.002890 | 0.000452 |
| 4 | 0.997299 | 0.939236 | 0.742831 | 0.459528 | 0.220442 | 0.083423 | 0.025450 | 0.006379 |
| 5 | 0.999850 | 0.987940 | 0.909347 | 0.718078 | 0.463654 | 0.242449 | 0.103626 | 0.036742 |
| 6 | 0.999996 | 0.998217 | 0.975300 | 0.883953 | 0.699616 | 0.466731 | 0.259984 | 0.121507 |
| 7 | 1.000000 | 0.999801 | 0.994663 | 0.961536 | 0.862377 | 0.685165 | 0.469139 | 0.274376 |
| 8 | 1.000000 | 0.999983 | 0.999069 | 0.989534 | 0.947731 | 0.843874 | 0.673456 | 0.471091 |
次の表は、攻撃側の期待利益を示しています。これは、pr(攻撃側の勝利数)*(防御側のダイス数)+pr(防御側の勝利数)*(攻撃側のダイス数-1)として定義されます。この表から、5の出目を持つ相手に対して8の出目を持つ攻撃をした場合、最大の期待利益が得られることがわかります。
攻撃側の勝利による純利益
| アタッカー | ディフェンダー | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 陸軍 | 2つの軍隊 | 3つの軍隊 | 4つの軍隊 | 5つの軍隊 | 6つの軍隊 | 7つの軍隊 | 8つの軍隊 | |
| 2 | 0.675926 | 0.331019 | -0.391976 | -0.820600 | -0.963370 | -0.994638 | -0.999432 | -0.999955 |
| 3 | 0.918982 | 1.114196 | 0.267875 | -0.849794 | -1.575009 | -1.880968 | -1.973990 | -1.995480 |
| 4 | 0.989196 | 1.696180 | 1.456986 | 0.216696 | -1.236464 | -2.249193 | -2.745500 | -2.929831 |
| 5 | 0.999250 | 1.927640 | 2.365429 | 1.744624 | 0.172886 | -1.575510 | -2.860114 | -3.559096 |
| 6 | 0.999976 | 1.987519 | 2.802400 | 2.955577 | 1.996160 | 0.134041 | -1.880192 | -3.420409 |
| 7 | 1.000000 | 1.998408 | 2.951967 | 3.615360 | 3.486147 | 2.221980 | 0.098807 | -2.158736 |
| 8 | 1.000000 | 1.999847 | 2.990690 | 3.884874 | 4.372772 | 3.970362 | 2.428384 | 0.066365 |
サイコロを最大 n 回振って Yahtzee を形成する確率はどれくらいですか?
他の読者のために、ヤッツィーとは5つのサイコロを使った5種類のサイコロの組み合わせです。ヤッツィーでは、プレイヤーは好きなサイコロを1つだけ持ち、残りのサイコロを振り直すことができます。最大3回まで振り直すことができます。
プレイヤーは希望に応じて、以前に保持していたサイコロを再度振り直すことができます。例えば、プレイヤーが最初に振った結果が3-3-4-5-6で、3の目を保持し、2回目に振った結果が3-3-5-5-5だった場合、5の目を保持し、3回目に振った結果が3の目だった場合、5の目を保持し、3回目に振った結果が3の目だった場合、再度振り直すことができます。
以下の表は、1回から20回までサイコロを振った場合の、同じ面のサイコロの最大数を示しています。この表から、3回振った場合のヤッツィーの出現確率は約4.6%であることがわかります。
ヤッツィーの確率
| ロール | 同じ面のサイコロの最大数 | ||||
|---|---|---|---|---|---|
| 1つ | 二 | 三つ | 4つ | 五 | |
| 1 | 0.092593 | 0.694444 | 0.192901 | 0.019290 | 0.000772 |
| 2 | 0.008573 | 0.450103 | 0.409022 | 0.119670 | 0.012631 |
| 3 | 0.000794 | 0.256011 | 0.452402 | 0.244765 | 0.046029 |
| 4 | 0.000074 | 0.142780 | 0.409140 | 0.347432 | 0.100575 |
| 5 | 0.000007 | 0.079373 | 0.337020 | 0.413093 | 0.170507 |
| 6 | 0.000001 | 0.044101 | 0.263441 | 0.443373 | 0.249085 |
| 7 | 0.000000 | 0.024501 | 0.199279 | 0.445718 | 0.330502 |
| 8 | 0.000000 | 0.013612 | 0.147462 | 0.428488 | 0.410438 |
| 9 | 0.000000 | 0.007562 | 0.107446 | 0.398981 | 0.486011 |
| 10 | 0.000000 | 0.004201 | 0.077416 | 0.362855 | 0.555528 |
| 11 | 0.000000 | 0.002334 | 0.055317 | 0.324175 | 0.618174 |
| 12 | 0.000000 | 0.001297 | 0.039279 | 0.285674 | 0.673750 |
| 13 | 0.000000 | 0.000720 | 0.027757 | 0.249063 | 0.722460 |
| 14 | 0.000000 | 0.000400 | 0.019543 | 0.215313 | 0.764744 |
| 15 | 0.000000 | 0.000222 | 0.013720 | 0.184883 | 0.801175 |
| 16 | 0.000000 | 0.000124 | 0.009610 | 0.157896 | 0.832371 |
| 17 | 0.000000 | 0.000069 | 0.006719 | 0.134258 | 0.858954 |
| 18 | 0.000000 | 0.000038 | 0.004692 | 0.113753 | 0.881517 |
| 19 | 0.000000 | 0.000021 | 0.003272 | 0.096100 | 0.900607 |
| 20 | 0.000000 | 0.000012 | 0.002280 | 0.080994 | 0.916714 |
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
サイコロを 2 つ振った場合、奇数と偶数のどちらの出目が多くなるのでしょうか?
答えは50/50です。これはサイコロを2個振った場合だけでなく、何個振った場合でも同じです。
少し話が逸れますが、クラップスで恐ろしい6/8の大きな賭けの代わりに、奇数/偶数の組み合わせの賭けが良い方法だとずっと思っていました。ハウスに有利になるように、私が提案する配当表と分析を以下に示します。
オッドベット
| イベント | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| 3または11 | 1.5 | 4 | 0.111111 | 0.166667 |
| 5または9 | 1 | 8 | 0.222222 | 0.222222 |
| 7 | 0.5 | 6 | 0.166667 | 0.083333 |
| 平 | -1 | 18 | 0.500000 | -0.500000 |
| 合計 | 36 | 1.000000 | -0.027778 |
イーブンベット
| イベント | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| 2または12 | 3 | 2 | 0.055556 | 0.166667 |
| 4または10 | 1 | 6 | 0.166667 | 0.166667 |
| 6または8 | 0.5 | 10 | 0.277778 | 0.138889 |
| 奇数 | -1 | 18 | 0.500000 | -0.500000 |
| 合計 | 36 | 1.000000 | -0.027778 |
この出版物に関するすべての権利は私が主張することをご承知おきください。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
ホットロールボーナスでは、プレイヤーは 2 つのサイコロの合計に応じて次の枚数のコインを獲得します。
- 2または12:1000
- 3または11:600
- 4または10:400
- 5または9:300
- 6または8:200
彼は合計7が出るまでサイコロを振り続け、ボーナスは終了します。最初のサイコロで7が出た場合、700コインの慰めの賞品がもらえます。ボーナスごとに獲得できるコインの平均枚数は?
平均ロール回数はボーナス終了イベントの逆数で、その確率は1/6です。つまり、プレイヤーは平均6回ロールすることになります。ただし、最後のロールは7回目となるため、ボーナスごとに平均5回の当選ロールが発生します。
次に、7 がないと仮定した場合の各合計の確率は次のとおりです。
- 2または12:1/30
- 3または11:2/30
- 4または10:3/30
- 5または9:4/30
- 6または8:5/30
したがって、7 が出ないと仮定した場合の 1 回のロールあたりの平均勝ちは、2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373.33 になります。
慰め賞金の価値は (1/6)*700 = 116.67 です。
したがって、平均ボーナス勝利額は 116.67 + 5×373.33 = 1983.33 となります。
プレイヤーが順番にサイコロを振り、出た目に基づいてサイコロを振ったプレイヤーだけが先に進むことができるとしたら、 「ウィザードに質問」コラム #179 のサイコロの問題の答えは何でしょうか?
コラム #179 に投稿された元の質問は次のとおりです: 2 つのサイコロを何度も振り、次のいずれかのイベントが発生するまで続けた場合、どちらが先に発生する可能性が高いでしょうか。
- 合計で 6 と 8 が出た場合、順序は問わず、重複も許可されます。
- 合計7が2回出ます。
あなたの工夫は、同じロールが両方のプレイヤーに有利にならないという点です。代わりに、プレイヤーは順番にロールし、ロールしたプレイヤーだけがそのロールを使えるようになります。
答えは誰が先にサイコロを振るかによって異なります。6と8が必要なプレイヤーが先にサイコロを振った場合、そのプレイヤーの勝率は57.487294%です。7が2つ必要なプレイヤーが先にサイコロを振った場合、6と8が必要なプレイヤーの勝率は52.671614%です。私は単純なマルコフ連鎖過程を用いてこの問題を解きました。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
6面サイコロを12個持っているとします。それらを振り、好きなサイコロを脇に置いておき、残りのサイコロをもう一度振ります。2回振って12の目が出る確率はどれくらいでしょうか?
最初のロールには58種類の出目があります。それぞれの出目は、最も多く出る面の数、次にその面のサイコロの合計数、というように分類します。例えば、3、3、3、3、6、6、6、5、5、2をロールした場合は、4-3-2-1と表記されます。次の表は、各出目の組み合わせの数、その出目が出る確率、2回目のロールで12の出目が完成する確率、そしてこれら2つの値の積を示しています。2回目のロールの確率については、プレイヤーが最初のロールで合計が最も大きいサイコロを持っていると仮定します。右下のセルには、全体の確率が0.0000037953、つまり263,486分の1であることが示されています。
12個のサイコロの質問
| 順序 | 組み合わせ | 確率 順序 | 条件付き 確率 | 合計 確率 |
|---|---|---|---|---|
| 12-0-0-0-0-0 | 6 | 0.0000000028 | 1.0000000000 | 0.0000000028 |
| 11-1-0-0-0-0 | 360 | 0.0000001654 | 0.1666666667 | 0.0000000276 |
| 10-2-0-0-0-0 | 1,980 | 0.0000009096 | 0.0277777778 | 0.0000000253 |
| 10-1-1-0-0-0 | 7,920 | 0.0000036384 | 0.0277777778 | 0.0000001011 |
| 9-3-0-0-0-0 | 6,600 | 0.0000030320 | 0.0046296296 | 0.0000000140 |
| 9-2-1-0-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 9-1-1-1-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 8-4-0-0-0-0 | 14,850 | 0.0000068220 | 0.0007716049 | 0.0000000053 |
| 8-3-1-0-0-0 | 237,600 | 0.0001091519 | 0.0007716049 | 0.0000000842 |
| 8-2-2-0-0-0 | 178,200 | 0.0000818639 | 0.0007716049 | 0.0000000632 |
| 8-2-1-1-0-0 | 1,069,200 | 0.0004911837 | 0.0007716049 | 0.0000003790 |
| 8-1-1-1-1-0 | 356,400 | 0.0001637279 | 0.0007716049 | 0.0000001263 |
| 7-5-0-0-0-0 | 23,760 | 0.0000109152 | 0.0001286008 | 0.0000000014 |
| 7-4-1-0-0-0 | 475,200 | 0.0002183039 | 0.0001286008 | 0.0000000281 |
| 7-3-2-0-0-0 | 950,400 | 0.0004366077 | 0.0001286008 | 0.0000000561 |
| 7-3-1-1-0-0 | 2,851,200 | 0.0013098232 | 0.0001286008 | 0.0000001684 |
| 7-2-2-1-0-0 | 4,276,800 | 0.0019647348 | 0.0001286008 | 0.0000002527 |
| 7-2-1-1-1-0 | 5,702,400 | 0.0026196464 | 0.0001286008 | 0.0000003369 |
| 7-1-1-1-1-1 | 570,240 | 0.0002619646 | 0.0001286008 | 0.0000000337 |
| 6-6-0-0-0-0 | 13,860 | 0.0000063672 | 0.0000214335 | 0.0000000001 |
| 6-5-1-0-0-0 | 665,280 | 0.0003056254 | 0.0000214335 | 0.0000000066 |
| 6-4-2-0-0-0 | 1,663,200 | 0.0007640635 | 0.0000214335 | 0.0000000164 |
| 6-4-1-1-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-3-3-0-0-0 | 1,108,800 | 0.0005093757 | 0.0000214335 | 0.0000000109 |
| 6-3-2-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000214335 | 0.0000001965 |
| 6-3-1-1-1-0 | 13,305,600 | 0.0061125083 | 0.0000214335 | 0.0000001310 |
| 6-2-2-2-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-2-2-1-1-0 | 29,937,600 | 0.0137531436 | 0.0000214335 | 0.0000002948 |
| 6-2-1-1-1-1 | 9,979,200 | 0.0045843812 | 0.0000214335 | 0.0000000983 |
| 5-5-2-0-0-0 | 997,920 | 0.0004584381 | 0.0000035722 | 0。0000000016 |
| 5-5-1-1-0-0 | 2,993,760 | 0.0013753144 | 0.0000035722 | 0.0000000049 |
| 5-4-3-0-0-0 | 3,326,400 | 0.0015281271 | 0.0000035722 | 0.0000000055 |
| 5-4-2-1-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-4-1-1-1-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-3-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-2-2-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-3-2-1-1-0 | 1億1975万4000 | 0.0550125743 | 0.0000035722 | 0.0000001965 |
| 5-3-1-1-1-1 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-2-2-2-1- | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 5-2-2-1-1-1 | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 4-4-4-0-0-0 | 69万3000 | 0.0003183598 | 0.0000005954 | 0.0000000002 |
| 4-4-3-1-0-0 | 24,948,000 | 0.0114609530 | 0.0000005954 | 0.0000000068 |
| 4-4-2-2-0-0 | 18,711,000 | 0.0085957147 | 0.0000005954 | 0.0000000051 |
| 4-4-2-1-1-0 | 74,844,000 | 0.0343828589 | 0.0000005954 | 0.0000000205 |
| 4-4-1-1-1-1 | 12,474,000 | 0.0057304765 | 0.0000005954 | 0.0000000034 |
| 4-3-3-2-0-0 | 49,896,000 | 0.0229219060 | 0.0000005954 | 0.0000000136 |
| 4-3-3-1-1-0 | 99,792,000 | 0.0458438119 | 0.0000005954 | 0.0000000273 |
| 4-3-2-2-1-0 | 2億9937万6000 | 0.1375314358 | 0.0000005954 | 0.0000000819 |
| 4-3-2-1-1-1 | 1億9958万4000 | 0.0916876238 | 0.0000005954 | 0.0000000546 |
| 4-2-2-2-2-0 | 37,422,000 | 0.0171914295 | 0.0000005954 | 0.0000000102 |
| 4-2-2-2-1-1 | 1億4968万8000 | 0.0687657179 | 0.0000005954 | 0.0000000409 |
| 3-3-3-3-0-0 | 5,544,000 | 0.0025468784 | 0.0000000992 | 0.0000000003 |
| 3-3-3-2-1-0 | 1億3,305万6,000 | 0.0611250826 | 0.0000000992 | 0.0000000061 |
| 3-3-3-1-1-1 | 44,352,000 | 0.0203750275 | 0.0000000992 | 0.0000000020 |
| 3-3-2-2-2-0 | 99,792,000 | 0.0458438119 | 0.0000000992 | 0.0000000045 |
| 3-3-2-2-1-1 | 2億9937万6000 | 0.1375314358 | 0.0000000992 | 0.0000000136 |
| 3-2-2-2-2-1 | 1億4968万8000 | 0.0687657179 | 0.0000000992 | 0.0000000068 |
| 2-2-2-2-2-2 | 7,484,400 | 0.0034382859 | 0.0000000165 | 0.0000000001 |
| 合計 | 2,176,782,336 | 1.0000000000 | 0.0000037953 |
平均して、公平なサイコロを各面を少なくとも 2 回振るには何回必要ですか?
答えについては下のボタンをクリックしてください。
これが私の解決策です。(PDF)
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
公平な6面サイコロを1、2、3、または6が出るまで振るとします。もし1、2、または3がこれらのゲーム終了の数字のうち最初に出たら、何も勝ちません。もし6がこれらのゲーム終了の数字のうち最初に出たら、サイコロを1回振るごとに1ドル勝ちます。このゲームの平均勝ち額はいくらでしょうか?
役に立つと思われる無限級数の数式をいくつかご覧になるには、下のボタンをクリックしてください。
ヒント1: i = 0から∞までのnの合計i = 1 / (1-n)
ヒント2: i = 0 から ∞ までの i × n の合計i = n / (1-n) 2
答えについては下のボタンをクリックしてください。
解決策については下のボタンをクリックしてください。
公平な6面サイコロを1、2、3、または6が出るまで振るとします。もし1、2、または3がこれらのゲーム終了の数字のうち最初に出たら、何も勝ちません。もし6がこれらのゲーム終了の数字のうち最初に出たら、サイコロを1回振るごとに1ドル勝ちます。このゲームの平均勝ち額はいくらでしょうか?
ヒント1: i = 0から∞までのnの合計i = 1 / (1-n)
ヒント2: i = 0 から ∞ までの i × n の合計i = n / (1-n) 2
期待される勝利は、i = 0 から ∞ までの (1 + i) * (1/3) i * (1/6) の合計として表すことができます。 =
(1/6) * (1/3) i の i = 0 から ∞ までの合計+ (1/6) * (i * (1/3) i ) の i = 0 から ∞ までの合計。
これらを一つずつ評価してみましょう。
i = 0から∞までの(1/3) i =の合計
1 / (1 - (1/3)) =
1 / (2/3) =
3/2
i = 0から∞までの(i * (1/3) i )の合計 =
(1/3) / (1 - (1/3)) 2 =
(1/3) / (4/9) =
(1/3) * (9/4) =
3/4
すべてをまとめると、答えは
(1/6) * (3/2) + (1/6) * (3/4) =
(1/4) + (1/8) =
3/8
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
公平なサイコロを振った場合、すべての面を少なくとも 2 回振る期待回数は何回ですか。
これは長くて面倒なマルコフ連鎖で解くこともできますが、私は積分解法を好みます。この手法の使い方については、ファイアベットとボーナスクラップスのページで説明しています。
重要な出来事がサイコロの目によって一つずつ決まるのではなく、一つの瞬間として捉えると想像してみてください。出来事間の時間は記憶を持たない性質を持ち、出来事間の平均時間は1単位時間であると仮定します。言い換えれば、出来事間の時間は平均1の指数分布に従います。賭けの判定においては、これは問題になりません。なぜなら、出来事は依然として一つずつ起こるからです。
ポアソン分布によれば、サイコロの任意の面がx単位時間内に0回振られる確率はexp(-x/6)*(x/6) 0 /0! = exp(-x/6) です。ポアソン分布によれば、任意の面がちょうど1回振られる確率はexp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6) です。したがって、任意の面がx単位時間内に2回以上振られる確率は1 - exp(-x/6)*(1 + (x/6))) 6です。少なくとも1つの面が2回以上振られていない確率は次の式で表されます。
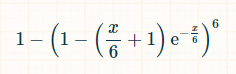
望ましい目標が達成されないまま平均してどのくらいの時間が経過するかを調べるには、これを全時間にわたって積分する必要があります。
幸いなことに、この時点で積分計算機を使うことができます。リンク先の計算機では、「積分を計算」の後のテキストボックスに 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 と入力し、カスタムで積分範囲を0から∞に設定します。
答えは390968681 / 16200000 = 約24.13386919753086です。
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
まず、公平な6面サイコロを6回振り、それぞれの出目を記録します。次に、これらの数字を、ラベルのない別の公平なサイコロの6面に書き込みます。例えば、6回振った結果が3、5、3、6、1、2だった場合、2回目のサイコロには4ではなく、3が2つ出ます。
次に、この2つ目のサイコロを6回振ります。その6つの数字を、さらに別の公平なサイコロの面に書き込み、前のサイコロから新しいサイコロを生成するというプロセスを続けます。
最終的に、6面全てに同じ目が出るサイコロになります。この状態に至るまでの、サイコロの出目遷移の平均回数(または合計出目を6で割った回数)はいくつですか?
混乱を避けるため、最初のサイコロには数字ではなく文字でラベルを付けましょう。それぞれのサイコロの状態にも文字を付けましょう。例えば、AAABBCは、ある文字が3つ、別の文字が2つ、そして別の文字が1つ出ていることを意味します。最初の状態は明らかにABCDEFです。
E(ABCDEF) を状態 ABCDEF からの期待ロール数とします。
E(ABCDEF) = 1 + [180 × E(AAAAB) + 450 × E(AAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656ある状態から別の状態へ遷移する組み合わせの数に基づいて、以下の遷移行列は、各初期状態(左の列)から各新しい状態へ遷移する方法が何通りあるかを示しています。ちなみに、これを正しく構築するには数時間かかりました。
遷移行列A
| 州 前に | ああああ | ああああ | ああああ | AAABBB | AAAABC | AAABBC | AABBCC | AAAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ああああ | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| ああああ | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| AAABBC | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| AABBCC | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| AAAABCD | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| AABBCD | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| AABCDE | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
行列代数についての長い講義はしませんが、行列 B は次のようになると仮定します。
マトリックスB
| 州 前に | ああああ | ああああ | AAABBB | AAAABC | AAABBC | AABBCC | AAAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| ああああ | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| ああああ | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| AABBCC | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| AABBCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| AABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
答えは行列 B と行列 A の行列式です。
決定(A) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000
決定(B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = 約9.65599148388557
1 つのサイコロを 20 回振った場合、6 つの面すべてが少なくとも 1 回出る確率はどれくらいでしょうか。
答えは、1 - (確率(1がない) + 確率(2がない) + ... + 確率(6がない)) = 1 - 6*(5/6)^20 = 約 0.84349568 と近似できます。
しかし、そうすると、2つの異なる面が出なかった状況が2回減算されてしまいます。6つの面から2つの面を選ぶ方法はcombin(6,2)=15通りあります。任意の2つの面が出なかった確率は(4/6)^20です。前のステップで2回減算されているので、この確率にこれらを加算する必要があります。つまり、1 - 6*(5/6)^20 + 15*(4/6)^20 = 約0.84800661となります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
しかし、一度も振られていない3つの面のグループが、最初のステップで3回減算され、2番目のステップで3回加算されていたとしたら、6つの面すべてが振られていない状態として、それらを減算し直す必要があります。6つの面から3つの面を選ぶ方法はcombin(6,3) = 20通りあります。特定の3つの面が一度も振られない確率は(3/6)^20です。つまり、1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 = 約0.847987537となります。
しかし、一度も振られていない4つの面のグループが、最初のステップで4倍減算され、2番目のステップで4倍加算され、3番目のステップで4倍減算されていたとします。これらの状態はそれぞれ既に2回減算されているため、これらを再び加算する必要があります。6つの面から4つの面を選ぶ方法はcombin(6,4) = 15通りあります。特定の4つの面が一度も振られない確率は(2/6)^20です。つまり、1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = 約0.84798754089となります。
しかし、もし20回振った目がすべて同じだった場合、この状況は最初のステップで5倍減算され、最初のステップで5倍加算され、3番目のステップで5倍減算され、4番目のステップで5倍加算されたことになります。これらを再び減算する必要があります。つまり、1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = 約0.84798754089となります。
したがって答えは1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = 約0.84798754089です。
サイコロが2つあります。両方のサイコロのそれぞれの面に、1以上の整数であれば好きな番号を付けることができます。同じサイコロに同じ目が何度も出たり、好きなだけ高い目が出たりしても構いません。標準的なサイコロを作る以外に、どのようにしてサイコロに番号を付ければ、どの合計が出る確率も標準的なサイコロと同じになるでしょうか?
サイコロ1 = 1、2、2、3、3、4。
サイコロ2 = 1、3、4、5、6、8。
残念ながら、この問題に対する私の解決策はかなり試行錯誤でした。
2 個のサイコロを振って 2 から 12 までの合計を出すのに必要な平均回数はいくつですか。
ドロップデッドは、5つの標準的なサイコロを使ってプレイするゲームです。プレイヤーは5つのサイコロを全て振ることから自分のターンを開始します。2と5が出なかった場合、サイコロの出目を合計し、その合計を自分のポイントスコアに加えて、もう一度サイコロを振ります。2または5が出た場合、そのロールのスコアは0になります。2または5が出たサイコロはすべてデッド(死)と宣言され、脇に置きます。残りのサイコロでもう一度サイコロを振ります。ゲームは、ポイントを獲得するか、サイコロを取り除いて続行されます。すべてのサイコロが除去された時点でターンは終了し、ドロップデッド(死んだ)とみなされます。すべてのロールのスコアが合計され、最終スコアが算出されます。高スコアのプレイヤーが勝ちます。
このゲームの予想スコアはいくらですか?
サイコロが 1 個残っているシナリオから始めて、後方へ進んでみましょう。
変数 a を、サイコロが 1 個残った場合に期待される追加ポイントとします。
2 または 5 以外の目が出る場合の平均は (1+3+4+6)/4 = 7/2 です。
a = (2/3)×(a + 7/2)。
a/3 = 7/3 です。
a = 7 です。
次に、サイコロが 2 個残ったときの期待値である b を計算します。
b = (2/3) 2 × (b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.
b = 11.2です。
次に、サイコロが 3 個残ったときの期待値 c を計算します。
c = (2/3) 3 × (c + 3× (7/2)) + 3×(2/3) 2 × (1/3)×b + 3×(2/3)×(1/3) 2 ×b。
c = 1302/95 = 13.705263 です。
次に、サイコロが 4 個残ったときの期待値 d を計算してみましょう。
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a。
d = 3752/247 = 15.190283.
最後に、残り 5 個のサイコロで予想されるポイント e を計算しましょう。
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a。
e = 16.064662 です。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
赤いサイコロと青いサイコロを2つ繰り返し振ります。それぞれのサイコロの出目の合計を記録します。2つのサイコロの合計が等しくなるまで、何個のサイコロを振ると予想されますか?
なぜ答えが無限大なのかを説明するのは難しい。さらに混乱を招き、逆説的なのは、合計が等しくなる確率が1であることだ。
次の表は、1 回目から 16 回目のロール後に初めて合計が同じになる確率を示しています。
確率合計が初めて等しくなる
| ロール | 確率 |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 13 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
Excel では、この曲線に非常に近い値は y = 0.1784*x-1.011 であると示されています。ここで、x = ロール回数、y = 確率です。
この無限級数の合計は無限大です。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
赤いサイコロ5個と青いサイコロ5個を振ります。順番に関係なく、両方のサイコロの出目が同じになる確率はどれくらいですか。例えば、両方のサイコロの出目が1-2-3-3-6の場合です。
次の表は、あらゆるタイプのロールについて示しています。
- このロールで出せるカードの組み合わせの数。例えば、フルハウスの場合、スリーカードの組み合わせは6通り、ペアの組み合わせは5通りあり、合計30通りのフルハウスが存在します。
- 順番の数。例えばフルハウスの場合、5個のサイコロのうち3個を選んでスリーカードにする方法はcombin(5,3)=10通りあります。残りの2個は必ずペアです。
- 与えられた手札の出目が何通りあるか。これは最初の2列の積です。例えば、フルハウスが出る可能性は30 * 10 = 300通りあります。
- ハンドの確率。例えば、フルハウスの確率は300/6 5 = 0.038580です。
- 両方の目が同じで、かつ与えられた役である確率。これは、4列目の確率の2乗を2列目で割ったものです。例えば、2回投げて両方ともフルハウスになる確率は0.038580 2です。しかし、同じハウスになる確率は1/30です。つまり、2回投げて両方とも同じフルハウスになる確率は0.038580 2 /30 = 0.00004961となります。
右下のセルには、両方のロールが同じになる合計確率が 0.00635324 であることがわかります。
マッチングロール
| タイプ ロールの | 違う 種類 | 注文 | 合計 組み合わせ | 確率 ワンロール | 確率 2つのロール | |
|---|---|---|---|---|---|---|
| 5枚の同じもの | 6 | 1 | 6 | 0.00077160 | 0.00000010 | |
| フォー・オブ・ア・カインド | 30 | 5 | 150 | 0.01929012 | 0.00001240 | |
| フルハウス | 30 | 10 | 300 | 0.03858025 | 0.00004961 | |
| スリーオブアカインド | 60 | 20 | 1,200 | 0.15432099 | 0.00039692 | |
| 2組 | 60 | 30 | 1,800 | 0.23148148 | 0.00089306 | |
| ペア | 60 | 60 | 3,600 | 0.46296296 | 0.00357225 | |
| 5人のシングルトン | 6 | 120 | 720 | 0.09259259 | 0.00142890 | |
| 合計 | 7,776 | 1.00000000 | 0.00635324 |
次のいずれかのイベントが発生するまで、6 面サイコロを振ります。
A) どちらの側も 6 回登場しました。
B) どの側面も少なくとも 1 回は登場しています。
イベント A が最初に発生する確率はどれくらいでしょうか?
この質問に私が答えたように微積分を使用して答えるには、 integral-calculator.com / にあるような積分計算機をお勧めします。
これが私の解決策です(PDF)。
この問題は、 Wizard of Vegasの私のフォーラムで (少し異なる言葉で) 質問され、議論されています。
普通の6面ダイスを使うゲームをしたいと思っています。残念ながら、ダイスを失くしてしまいました。しかし、4枚のインデックスカードがあり、好きなように印を付けることができます。プレイヤーは4枚のカードからランダムに2枚を選び、その合計を求めます。
2 枚の異なるカードの合計がサイコロの出目を表すように、カードに番号を付けるにはどうすればよいでしょうか。
0、1、2、4 と番号を付けます。
4 枚のカードから 2 枚を引く方法は、次の 6 通りあります。
- 0+1 = 1
- 0+2 = 2
- 1+2 = 3
- 0+4 = 4
- 1+4 = 5
- 2+4 = 6
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
6面サイコロを何度も振り、出た目の合計が13以上になるまで繰り返します。最終的な合計の平均値、中央値、最頻値はいくらですか?
中央値 = 14
モード = 13
この問題はマルコフ連鎖を使う必要がありました。次の表は、左の列の累積合計に応じて、それぞれの最終合計の確率を示しています。まず、合計が13から18の明らかなケースから始めましょう。次に、累積合計が0から12の場合は、下の6つのセルの平均を取ります。
初期状態の確率は、合計が 0 の最初の行にあります。
マルコフ連鎖
| ロールの合計 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|
| 0 | 0.279263 | 0.236996 | 0.192313 | 0.145585 | 0.097371 | 0.048472 |
| 1 | 0.290830 | 0.230791 | 0.188524 | 0.143842 | 0.097114 | 0.048899 |
| 2 | 0.293393 | 0.241931 | 0.181893 | 0.139625 | 0.094943 | 0.048215 |
| 3 | 0.289288 | 0.245178 | 0.193717 | 0.133678 | 0.091410 | 0.046728 |
| 4 | 0.280369 | 0.242560 | 0.198450 | 0.146988 | 0.086950 | 0.044682 |
| 5 | 0.268094 | 0.235687 | 0.197878 | 0.153768 | 0.102306 | 0.042267 |
| 6 | 0.253604 | 0.225827 | 0.193419 | 0.155611 | 0.111500 | 0.060039 |
| 7 | 0.360232 | 0.193566 | 0.165788 | 0.133380 | 0.095572 | 0.051462 |
| 8 | 0.308771 | 0.308771 | 0.142104 | 0.114326 | 0.081919 | 0.044110 |
| 9 | 0.264660 | 0.264660 | 0.264660 | 0.097994 | 0.070216 | 0.037809 |
| 10 | 0.226852 | 0.226852 | 0.226852 | 0.226852 | 0.060185 | 0.032407 |
| 11 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.027778 |
| 12 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 |
| 13 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 14 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 15 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 |
| 16 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 |
| 17 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 |
| 18 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
この質問は私のフォーラム「Wizard of Vegas」で尋ねられ、議論されています。
ご存知のように、クラップスの「オール」ベットは、7 以外の 2 から 12 までのすべての合計が 7 が出る前に出れば勝ちます。このベットで勝つには、平均して何回ロールする必要がありますか?
クラップスのテーブルで18回連続(合計11回)の目撃者がいると主張している人がいます。それを観察するには平均して何回ロールすればいいのでしょうか?
これが私の解決策です(PDF)。
2 つの 6 面サイコロを 1 組として、次の 2 つのイベントのいずれかが発生するまで繰り返し振ります。
A) 合計12が出ます。
B) 合計 7 が 2 回連続して出ます。
どちらが先に起こる可能性が高いでしょうか?
> [spoiler=解決策]
させて:
- p = 初期状態から最初に 12 が出る確率、または前回のロール結果が 7 でなかったときの確率。
- q = 前回のロール結果が 7 だった場合に、最初に 12 が出る確率。
これはマルコフ連鎖問題として知られています。
その前に、合計が 7 になる確率は 1/6 で、12 になる確率は 1/36 であることを思い出してください。
p と q は次のように相互に定義できます。
- (1) p = (1/36) + (6/36)q + (29/36)p
- (2)q = (1/36)+ (29/36)p
式(1)に36を掛けてみましょう。
36p = 1 + 6q + 29p
(3)7p = 1 + 6q
(2)のqの値を(3)に代入してみましょう。
7p = 1 + 6*((1/36) + (29/36)p)
7p = 1 + (1/6) + (29/6)p
42ペンス = 6 + 1 + 29ペンス
13ペンス = 7
q = 7/13
したがって、最初に 12 が出る確率は 7/13 =~ 53.85% です。
したがって、最初に 2 回連続して 7 が出る可能性は 46.15% です。
したがって、最初に合計 12 が出る可能性が高くなります。



