WOO logo

Wizard のオススメ

確率 - 一般的な質問

長期的には、何をしてもどのカジノゲームでも負けてしまうと言うのですか?

Joe から Harrisburg, US

ブラックジャックやビデオポーカーで稀に期待値がプラスになるチャンスがあるという例外を除けば、はい、それが私が言っていることです。

確率を x から y の形式に変換するにはどうすればよいでしょうか?

Ralph Harpster から Turlock, USA

ある出来事が起こる確率がx対yであるということは、その出来事がy回起こらないごとにx回起こることを意味します。これを変換するには、ある出来事が起こる確率をpとします。この確率は(1/p)-1対1と表すこともできます。例を見てみましょう。ファイブカードスタッドでフルハウスを引く確率は0.00144058です。これは693.165対1と表すこともできます。

最近、開催されていたフットボールプールを見ていました。これは、100個のマス目があり、X軸とY軸に沿って0から9までの数字が並び、スコアの最後の数字に対応するタイプのものでした。私はフットボールファンではないので、このプールには賭けませんでしたが、ギャンブラーなので、それほど魅力的な賭けではないと思っています。

私が言及しているプールの種類をご存知だと仮定しています。各ボックスの価格は5ドルで、配当は四半期ごとに支払われます。ボックスが当たれば125ドルの賞金がもらえますが、最後の数字が同じであれば4四半期すべて当選して500ドルを獲得し、配当は100対1になる可能性があります。

賭けを勧誘した人は、500ドルの当選確率は100対1だと言っていましたが、私は同意しません。まず、0と7のボックスは2と9のボックスよりも当選確率がはるかに高いです。しかし、ゲーム全体を通して最後の2つの数字が0と7のままになる確率は高いはずです。もしボックスがランダムに選ばれるとしたら、500ドルの賞金が当たる確率はどれくらいでしょうか？

Sam から Phillipsburg, USA

グリッド内のセルがランダムに選択されると仮定すると、いずれかの四半期で勝利する確率は1/100になります。各四半期が独立したイベントであると仮定すると（実際にはそうではありませんが）、4つの四半期すべてで勝利する確率は(1/100) 4 = 1億分の1になります。

12対1や3対2といったオッズの読み方を知りたいです。12対1と3対2のどちらの方が勝つ確率が高いでしょうか？

Louis から Montreal, Canada

確率をそのような形で使うのは好きではありませんが、一般的には「ロイヤルフラッシュが出ない確率は649,739対1です」といった構文で使われます。つまり、ロイヤルフラッシュが出ない確率は649,739通りあり、出せる確率は1通りあるということです。あなたの例では、12対1は1/13、つまり7.69%、3対2は2/5、つまり40.00%なので、3対2の方が勝つ確率が高いということになります。

セントルイス・ポスト・ディスパッチ紙の記事で、記者はこう述べています。「500年に一度の洪水とは、ある年に500分の1の確率で発生する洪水のことです。言い換えれば、50年間で10分の1の確率、1世紀で5分の1の確率で発生するということです。」ギャンブルに関するページを全部読んでみて、これは正しい言い方ではないと思いました。彼らの主張を推論すると、500年に一度洪水が発生する確率が1分の1であるということになりますが、それは全く正しくありません。

匿名

ご指摘の通り、その記事は誤りです。x年間に500年に一度発生する洪水の確率は1-e -x/500です。つまり、50年間に少なくとも1回500年に一度発生する確率は9.52%、100年間に発生する確率は18.13%です。

ゲームのフェアラインを-160/+160と判定し、-145というローグラインを発見した場合、私のEVはいくらになりますか？フェアラインを判定した後にEV +/-を算出できる計算式があれば教えていただけると大変助かります。

匿名

優勝候補が勝つ確率をpとする。-160がフェアラインだとすると、次のようになる。

100*p - 160*(1-p) = 0
260p = 160
p = 160/260 = 8/13 = 61.54%。

つまり、-145ラインで$145を賭けた場合の期待リターンは、(8/13)*100 + (5/13)*-145 = 75/13 = $5.77となります。つまり、プレイヤーのアドバンテージは$5.77/$145 = 3.98%となります。

tをハウスエッジなしの真のマネーライン、aを実際のマネーラインと定義しましょう。プレイヤーの期待収益率の計算式は以下のとおりです。

Aは負で、tも負です: (100*(ta) / (a*(100-t))
Aは正、tは正: (at)/(100+t)
Aは正、tは負: (a*t + 10000)/((t-100)*100)

したがって、あなたの場合、期待収益は 100*(-160 -(-145))/(-145*(100-(-160))) = 3.98% となります。

2000 年にゴアに投票した郡がすべて、最近フロリダを襲った 3 つのハリケーンによる被害を免れたという事実によって証明されている、神は民主党員であるという以下の主張について、どう思われますか。

匿名

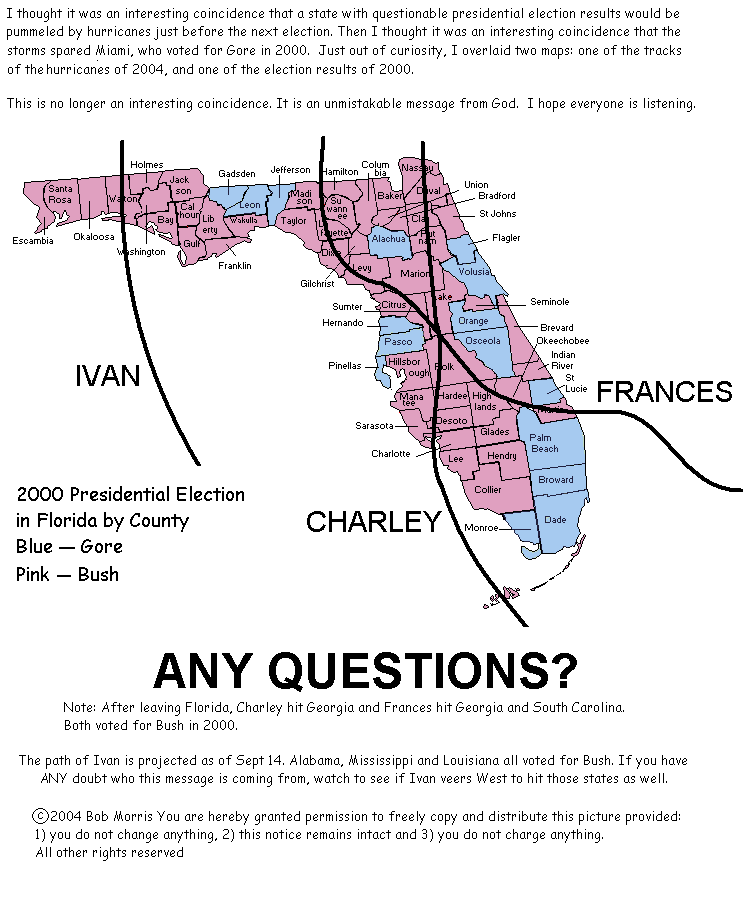
まず、著者が末尾で許可を与えているため、これを公開します。これは、相関関係が必ずしも因果関係を意味するわけではないという良い例です。過去を振り返ると、多くの偶然の一致を見つけるのは簡単です。何かを主張するには、証拠を集める前に仮説を立てるべきです。

追記（2004年11月13日）：別の読者から、この地図は当初はジョークとして作られたものが都市伝説に変わってしまったと指摘がありました。このリンク先で指摘されているように、地図上のハリケーンの進路は単に正確ではなく、実際のハリケーンはゴア郡の多くの地域を襲いました。これは、特にインターネット上で目にする情報は、全てを信じるべきではないということを示しています。

ちょっと興味があるかもしれないと思い、こちらに賭けました。Bodogで「ブリトニー・スピアーズとケビン・フェダーラインの第二子は男の子？女の子？」という賭けが提供されています。男の子なら+105、女の子なら-145です。私が最後に調べたところ、人類が始まって以来、このオッズは1:1でした。-145のオッズに賭ける人は誰ですか？ぜひ教えてください。このサイトを気に入っていただけたら、ぜひ頻繁にアクセスして、スポンサーへの感謝の気持ちとしてクリックしてください。

匿名

温かいお言葉、ありがとうございます。正直なところ、クリック率なんてもう誰も気にしていません。ですから、バナーが見せかけだけのものなら、無理にクリックする必要はありません。ご質問にお答えすると、アメリカでは男の子が生まれる確率は50.5%、女の子が49.5%と非常に近いです。賭け事のコミュニティに他の情報が何も知られていないと仮定すると、男の子に賭けたプレイヤーのアドバンテージは0.505*1.05 - 0.495 = 3.53%となります。内部情報を持つ誰かが女の子に賭けているのかもしれません。別の説としては、母親のお腹の形で性別がわかると誤解している人がいて、女の子に賭けているというものがあります。個人的には、この件については触れないことにします。

このYouTube動画で、マット・デイモンはジョン・マケインが最初の任期を全うできない確率は3分の1だと言っています。彼の言う通りでしょうか？

Lisa から San Antonio, TX

いいえ。CDC（疾病予防管理センター）のこの生命表によると、72歳の白人男性が76歳まで生きる確率は85.63%です。これは約7分の1の確率で死亡することを意味します。生存率は、14ページの白人男性の表にある76歳出生コホート57,985人を、72歳出生コホート67,719人で割ることで算出できます。ここで使用している表は「期間生命表」と呼ばれ、2003年の死亡率が将来も変わらないと仮定した、最も一般的な生命表です。完璧主義者なら1936年のコホート生命表を使いたがるかもしれませんが、それほど大きな違いはないと思います。

追伸：この回答を投稿した後、私の回答はジョン・マケイン氏の個人的な健康状態を考慮していないというコメントを複数いただきました。彼にとって不利なのは、彼が癌サバイバーであることです。有利なのは、お金で買える最高の医療を受けられること、72歳にしては明らかに精神的にも肉体的にも良好な状態であること、そして母親が健在であることからもわかるように長生きであることです。しかし、私はこの情報を考慮に入れるつもりはありませんでした。私が言及していたのは、マット・デイモンが引用した保険数理表のことです。私が言いたいのは、平均的な72歳の白人男性が今後4年間生存する確率は86%だということです。強いて言えば、ジョン・マケイン氏の確率はそれよりもさらに高いと予測します。

同じ量の紙がある場合、円筒形の紙コップと円錐形の紙コップのどちらに多くの水が入りますか？円筒形のコップは片側が開いており、どちらの場合も寸法が最適であると仮定します。

匿名

答えと解決方法については、私の関連サイトMathProblems.info の問題番号 210 を参照してください。

ニュージャージー州ポップコーンパーク動物園のラクダ「プリンセス」の話をご存知ですか？NFLのハンディキャップスプレッドで88勝51敗という記録を樹立しています。そのオッズはどれくらいでしょうか？

匿名

プッシュを除けば、139回のピックのうち88勝以上を挙げる確率は0.00107355、つまり931分の1です。これはかなり期待外れです。きっと、誰も記事にしていない、もっと悪い成績を収めた動物が930匹もいるでしょう。プリンセスについてもっと知りたい方は、ESPN.comの記事「ニュージャージーのラクダがジャイアンツがペイトリオッツに勝つと予想」をご覧ください。

2012年5月8日の「チェルシー・レイトリー」番組で、チェルシーは赤毛の動物は互いに交尾しないため絶滅しつつあると発言しました。これは本当でしょうか？

匿名

あなたが幸せであることを願います。これには何時間も費やしました。

この疑問に答えるには、チェルシー・ハンドラーの赤毛仮説に基づく行動を定量化することが重要です。私の仮定は以下のとおりです。

  1. 赤い頭の動物は、決して他の赤い頭の動物と交尾することはありません。
  2. メスは常に交尾相手としてオスを選びます。
  3. 誰もが交尾し、交尾ごとに同じ数の子供が生まれます。
  4. 赤毛のメスは、赤毛でないメスの中からランダムに選び、最初に交尾相手を選ぶ権利を持ちます。
  5. 赤毛遺伝子を持つ女性（赤毛遺伝子を 1 つ持つ）は、赤毛の男性が残した男性の中からランダムに配偶者を選びます。
  6. 陰性の女性（赤毛遺伝子を持たない）は、赤毛の男性と保因者が残した男性の中からランダムに選択します。

「Today I Found It」によると、赤毛の確率は4%です。そして、これまで赤毛に対する偏見はなかったと仮定します。

赤毛に対する偏見が次の世代から始まり、そして続くと仮定すると、赤毛を持つ人口全体の傾向はどうなるでしょうか？スプレッドシートで多くの作業を行いましたが（詳細は割愛します）、この世代から始まる最初の8世代は以下のとおりです。

赤毛の割合

世代割合
1 4.000000%
2 3.888889%
3 3.895219%
4 3.894863%
5 3.894883%
6 3.894882%
7 3.894882%
8 3.894882%

3世代目までに赤毛の人口の割合は3.90%に収束する見込みです。ですから、チェルシーが何を言おうと、赤毛の人たちは心配する必要はないと思います。

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。
CardPlayer.comによると、2013年のワールドシリーズ・オブ・ポーカーで決勝に進出した9人のプレイヤーの一人であるアミール・レハヴォットは、9位入賞の最低賞金73万3224ドルを超える賞金を、1%の株式につき2万9248ドルで売却しているという。これは公正な価格だろうか？

匿名

まず、チップスタックを確認しましょう。

2013 WSOP ファイナルテーブル チップスタック

プレーヤーチップス
JCトラン38,000,000
アミール・レハヴォット29,700,000
マーク・マクラフリン26,525,000
ジェイ・ファーバー25,975,000
ライアン・リース25,875,000
シルヴァン・ルースリ19,600,000
ミヒール・ブルメルハウス11,275,000
マーク・ニューハウス7,350,000
デビッド・ベネフィールド6,375,000

次の表は、トーナメントの各最終結果の勝敗を示しています。

2013 WSOPファイナルテーブル賞金

場所勝つ
1位8,359,531ドル
2位5,173,170ドル
3位3,727,023ドル
4番目2,791,983ドル
5番目2,106,526ドル
6番目1,600,792ドル
7日1,225,224ドル
8日944,593ドル
9日73万3224ドル

各プレイヤーのスキルが同等だと仮定すると、勝利確率はチップスタック全体のシェアとして推定できます。しかし、それ以降のポジションでは計算はより複雑になります。この疑問に答えるために、私はポーカートーナメント計算機を開発しました。

上記の情報を入力すると、Amirの予想賞金は3,658,046ドルであることがわかります。9位の最低賞金733,224ドルを差し引くと、期待される非保証賞金は2,924,822ドルになります。1%の株式の価値は29,248.22ドルです。これはcardplayer.comの記事で引用されている価格とほぼ同じです。

ちなみに、レハヴォットは3位で、賞金は3,727,023ドルでした。9位の保証金733,224ドルを差し引いて100で割ると、1%の株式あたり29,938ドルの利益となります。1株あたりの原価は29,248ドルだったので、1株あたり2.36%の利益が出たことになります。

この質問はWizard of Vegasの私のフォーラムで議論されています。

プレイヤーのデスクでチケットを印刷し、それをドラムに入れるという、電子チケットではなく、通常のドラムに入った通常のチケットを使用するカジノのプロモーションでは、ドラムに入れる前にチケットを曲げたり、折り目をつけたりしていますか？ 折り目がついたチケットの方が当選確率が高いと思いますか？

AxiomOfChoice

皆さんが幸せでありますように。この質問に答えるために、オフィス・デポで大きなチケットのロールを買いました。そのうち500枚を紙袋に入れ、半分は90度くらいの角度で半分に折り、もう半分は広げておきました。そして、6人のボランティアにそれぞれ40～60枚ずつ、順番を入れ替えながら引いてもらい、結果を記録しました。結果は以下の通りです。

抽選チケット実験

主題折り畳まれた展開合計
1 25 25 50
2 38 22 60
3 25 15 40
4 34 16 50
5 27 23 50
6 26 24 50
合計175 125 300


つまり、抽選されたチケットの 58.3% が折り返されたことになります。

フォールドが影響しないと仮定した場合、これらの結果は期待値から標準偏差2.89倍離れることになります。フォールドがオッズに影響を与えないと仮定した場合、この枚数、あるいはそれ以上のフォールドされたチケットが当たる確率は0.19%、つまり514分の1です。

さらに付け加えると、急いでチケットを引いた被験者は、折り紙付きのチケットを引く可能性がはるかに高かった。一方、時間をかけて慎重に引いた被験者は、その確率はほぼ50/50であった。

だから、私の結論は、間違いなく折りたたむことです。

この質問についての議論については、 Wizard of Vegasの私のフォーラムをご覧ください。

2人のプレイヤーにそれぞれ(0,1)の範囲の乱数が配られます。最初のプレイヤーはそのまま続けるか、カードを捨てて新しい数字を引くかを選択します。2番目のプレイヤーも同様にカードを引きます。高い数字を引いたプレイヤーが勝ちます。各プレイヤーにとって最適な戦略は何でしょうか？最適な戦略を前提とした場合、各プレイヤーが勝つ確率はどれくらいでしょうか？

Joe Shipman から New Jersey

いい質問ですね！こちらが私の回答と簡単な解決策です。PDF形式の解決策もご覧ください。

コインを投げるゲームをする機会が与えられたとしましょう。1回目が表なら2ドル戻ってゲームオーバーです。そうでなければ、もう一度投げます。2回目も表なら4ドル戻ってきます。2回目も裏なら、表が出るまで投げ続けます。1回投げるごとに賞金は2倍になります。つまり、2のn乗が戻ってきます。ここでnはコインを投げた回数です（最後に表が出たときも含みます）。このゲームをするのにいくら払いますか？数学的な答えは無限大だと聞きますが、それは理にかなっていません。なぜなら、いつかは有限の金額を勝ち取らなければならないからです。

Omaha

これはサンクトペテルブルクのパラドックスとして知られています。

確かに、このゲームの期待勝利額は無限大ですが、同時に、コインが最終的に裏になり、最終的に得られる金額が有限になる確率も存在します。期待勝利額の計算は以下のとおりです。

期待勝利数 = pr(1回)×2 + pr(2回)×4 + pr(3回)×8 + pr(4回)×16 + pr(5回)×32 + pr(6回)×64 + ... =

(1/2) 1 × 2 1 + (1/2) 2 × 2 2 + (1/2) 3 × 2 3 + (1/2) 4 × 2 4 + (1/2) 5 × 2 5 + (1/2) 6 × 2 6 + ...

= ((1/2)*(2/1)) 1 + ((1/2)*(2/1)) 2 + ((1/2)*(2/1)) 3 + ((1/2)*(2/1)) 4 + ((1/2)*(2/1)) 5 + ((1/2)*(2/1)) 6 + ...

= 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + ...

= 1 + 1 + 1 + 1 + 1 + 1 + ... = ∞

プレイヤーが勝ち取るべき金額は有限であるのに、期待される勝利金額は無限であるという点が逆説的です。どうしてそうなるのでしょうか？

あまり納得のいく答えではないかもしれませんが、∞には多くのパラドックスが存在します。怒りのメールが届くかもしれませんが、そうした無限のパラドックスにもかかわらず、私が夜眠れるのは、∞が現実の物理宇宙において存在が証明されていない数学的または哲学的な概念であると信じているからです。この無限の概念、あるいは理論には、内在するパラドックスが内在しているのです。

これに反対する方は、無限の量や測定が証明されているものがあれば教えてください。ブラックホールの大きさの証拠がない限り、ブラックホールの密度が無限だなどと言わないでください。

このゲームにいくら払うべきかという最初の疑問に答えるためには、幸福度は金額に比例しないということを念頭に置く必要があります。私は経済学の授業で、お金から得られる効用、つまり幸福度は金額の対数に比例すると教わり、その考えに至りました。この仮定のもと、最初の資産がゼロの場合を除いて、二人の資産が同じ割合で増減した場合、二人とも幸福度の変化は同じになります。例えば、ジムの資産が突然1,000ドルから1,100ドルに増加し、ジョンの資産が突然10,000,000ドルから11,000,000ドルに増加した場合、二人とも幸福度は同じに増加します。なぜなら、どちらの場合も資産が10%増加したからです。お金から得られる幸福度が実際に金額の対数に比例すると仮定すると、次の表は、誰かがゲームにお金を払う前に、資産に応じて支払う意思のある最高額を示しています。

無関心は遊ぶ量

富無関心
額
10ドル4.97ドル
100ドル7.79ドル
1,000ドル10.96ドル
1万ドル14.26ドル
10万ドル17.78ドル
100万ドル20.88ドル
1000万ドル24.19ドル
1億ドル27.51ドル
10億ドル30.84ドル


ご覧の通り、現実的な状況では、支払うべき金額は$∞よりもはるかに少ないです。例えば、資産が100万ドルの場合、$20.88でプレイしても問題ないでしょう。

この質問は、 Wizard of Vegasの私のフォーラムで提起され、議論されています。

ミシガン州宝くじには、次のルールの 3 人用ゲームがあります。

  1. プレイヤーは1人ずつプレイし、まだプレイしていないプレイヤーはステージから退場させられ、前のプレイヤーのプレイ状況に関する情報は与えられません。100
  2. 枚のカードがあり、それぞれ1から100までの番号が付け
    3. られ
  3. ています。プレイヤーは最初に好きなカードを選びます。
  4. カードを確認した後、そのカードを保持するか、新しいカードと交換するかを
  5. 選択できます。すべてのカードは交換されます。つまり、古いカードは捨て札を含め、デッキに戻されます。
  6. 最も高い数字のカードを引いたプレイヤーが勝ちます。


このゲームで後攻に有利なポジションはありますか？各プレイヤーにとって最適な戦略は何でしょうか？

このゲームの様子を映したYouTube動画をご覧ください。

Dween

まず、最後にプレイしても位置的な有利性はありません。前のプレイヤーがプレイしている間、プレイヤーは防音ブース内にいるので、順番は関係ありません。

第二に、ゲームにはナッシュ均衡が存在し、少なくともx点のスコアで勝利する戦略が他のどの戦略よりも優れている必要があります。問題はx点を見つけることです。

私がしたのは、1から100までの番号が書かれたカードの代わりに、各プレイヤーが0から1までの一様分布の乱数を受け取り、完璧な論理学者がスタンドとスイッチのどちらにも無差別となる点xを探すという戦略を立てることです。この答えがあれば、1から100までの離散分布に簡単に適用できます。

ここまでで話は終わりにして、読者の皆さんに問題を解いてもらいます。答えと解答については、以下のリンクをご覧ください。

0 から 1 までの連続分布の答え。

1 から 100 までの離散分布に対する回答。

私の解決策については、ここをクリックしてください（PDF） 。

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。

赤いカード10枚と黒いカード10枚が入ったデッキがあるとします。ランダムシャッフル後、カードを元に戻さずに引きます。赤いカード5枚よりも先に黒いカードを10枚すべて引く確率はどれくらいでしょうか？

Don

これは、ランダムに選んだ14枚のカードに10枚全て黒いカードが含まれている確率を問うのと同じです。デッキの10枚のうち赤いカードを4枚選ぶ方法は、(10,4)=210通りあります。もちろん、10枚の黒いカード全てを選ぶ方法は1通りしかありません。20枚のうち14枚を選ぶ方法は、(20,14)=38,760通りあります。つまり、答えは210/38,760=0.005418、つまり184.57分の1です。

13ランクすべてでフォーカードを達成するとボーナスが支払われるプロモーションを知っています。平均して何ハンドかかりますか？

AxelWolf

あなたの質問に答えるために、ビデオポーカーのゴールドスタンダードである「9-6ジャックス オア ベター」を見てみましょう。

最初のステップは、計算機を改造して、13種類のフォー・オブ・ア・カインドすべてに対応する項目を追加することです。改造後のリターン表は以下のとおりです。

修正されたジャックス・オア・ベターのリターンテーブル

イベント支払う組み合わせ確率戻る
ロイヤルフラッシュ800 4億9351万2264円0.000025 0.019807
ストレートフラッシュ50 2,178,883,296 0.000109 0.005465
4A 25 3,900,253,596 0.000196 0.004892
4K 25 3,904,533,816 0.000196 0.004897
4つのQ 25 3,898,370,196 0.000196 0.004889
4つのJ 25 3,886,872,684 0.000195 0.004875
4 10 25 3,471,687,732 0.000174 0.004354
4つの9 25 3,503,226,684 0.000176 0.004394
4つの8 25 3,504,128,652 0.000176 0.004395
4 7 25 3,504,825,252 0.000176 0.004396
4 6 25 3,504,861,888 0.000176 0.004396
4 5 25 3,504,895,944 0.000176 0.004396
4 4 25 3,504,032,676 0.000176 0.004395
4 3 25 3,503,177,148 0.000176 0.004394
4 2 25 3,502,301,496 0.000176 0.004393
フルハウス9 229,475,482,596 0.011512 0.103610
フラッシュ6 219,554,786,160 0.011015 0.066087
真っ直ぐ4 223,837,565,784 0.011229 0.044917
スリーオブアカインド3 1,484,003,070,324 0.074449 0.223346
2組2 2,576,946,164,148 0.129279 0.258558
ジャック以上1 4,277,372,890,968 0.214585 0.214585
何もない0 10,872,274,993,896 0.545435 0.000000
合計19,933,230,517,200 1.000000 0.995439


フォー・オブ・ア・カインドが出る確率は 0.002363 です。

次に答えなければならないのは、13種類全て揃えるには平均して何回のフォー・オブ・ア・カインドが必要かということです。この質問に答えるために、期待試行回数計算機を作成しました。この計算機を使うには、最初の13個のセルに各フォー・オブ・ア・カインドの組み合わせの数を入力します。計算機は、13種類全て揃えるには平均で41.532646回のフォー・オブ・ア・カインドが必要であると計算します。

したがって、13 枚のフォー・オブ・ア・カインドすべてを獲得するために必要なハンドの予想数は、41.341739/0.002363 = 17,580 です。

草原は正確には次のものを供給できます。

牛1頭とラマ1頭を21日間。
ラマ1頭と羊1頭を42日間。
羊1頭と牛1頭を28日間飼育します。
牛はラマと羊を合わせたのと同じくらいの量の草を食べます。
草は一定の速度で成長します。

3 匹の動物が一緒に草原を完全に食べ尽くすには、どれくらいの時間がかかるでしょうか?

MatiX

[ネタバレ] では:
c = 牛が草を食べる割合
l = ラマが草を食べる割合
s = 羊が草を食べる割合
g = 草の成長速度

一定期間の終わりには、消費した草の量は、最初の草の量とその期間に生育した草の量の合計と等しくなければなりません。つまり…

（1）21*（c+l）= 1 + 21g
（2）42*（l+s）=1+42g
（３）28*（s+c）=1+28g

ここで、1 は 1 つの芝生のフィールドを表します。

また、次のことも与えられています。

(4) c=s+l

まず、式(4)を式(2)に代入します。

（5）42c = 1 + 42g

これをgで表すと次のようになります。

(6) g = (42c-1)/42

次に式(6)を式(1)に代入します。

(7) 21(c+l) = 1 + 21*(42c-1)/42

少し代数を計算してみると次のようになります...

（８）l = 1/42。

次に式(4)を式(3)に代入します。

（9）28*（2s + l）= 1+28g

l=1/42 であることがわかっているので...

28*(2s + 1/42) = 1+28g
56秒 + 28/42 = 1 + 28g
2352秒 + 28 = 42 + 1176グラム
(10) g = (2352s - 14)/1176

次に、式(8)と式(10)を式(2)に代入します。

42*(1/42 + 秒) = 1 + 42*(2352秒 - 14)/1176

簡単な代数計算をすると次のようになります。

（11）s = 14/1176 = 1/84

式（4）より

（12）c = （1/84）+ （1/42）= 3/84 = 1/28

つまり、草が育たなかったら、畑の草を食べるのに牛は28日、ラマは42日、羊は84日かかります。

次にgについて解いてみましょう。(11)を(10)に代入します。

g = [2352*(1/84)- 14]/1176
（13）g = 14/1176 = 1/84。

偶然にも、これは羊が草を食べる割合と同じです。

最終的な答えをtとしましょう。t日間で食べられた草の量は、畑の草の量(1)とその期間に生育した草の量の合計に等しくなるはずです。つまり…

（13）t*（s+l+c）= 1 + tg

t を解決します...

t*[(1/84) + (1/42) + (1/28)] = 1 + t/84
t = 1/[(1/84) + (1/42) + (1/28) - (1/84)]
（14）t = 84/5 = 16.8日 = 16日19時間12分

[/spoiler]

この質問は、Wizard of Vegas の私のフォーラムで提起され、議論されました。

単位正方形内の 2 つのランダムな点間の平均距離はどれくらいですか?

匿名

こんなに簡単な質問なのに、解くのはかなり複雑です。私がやった方法では、この積分を知っておく必要があります。

ここに答えと私の解決策（PDF）があります。

映画『グッド・ウィル・ハンティング』の黒板に書かれていた数学の問題は何でしたか？

匿名

MITの組み合わせ数学の授業にしては、実はかなり簡単でした。問題の文言は次のとおりです。

「サイズ n=10 の同相的に既約な木をすべて描画します。」

これを平易な英語で説明してみることにします。

直線のみを使って、交差点と行き止まりの合計が10となる図形をすべて描きます。閉じたループはあってはなりません。また、2つの同値な図形があってはなりません。交差点からは、少なくとも3本の線が伸びている必要があります。

「同等」とはどういう意味でしょうか？ 交点をそのままにして、ピースを好きなように動かしても、新しい図形は作成されないという意味です。

次に例を示します。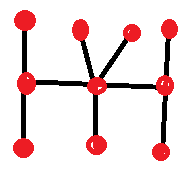



ヒントをあげましょう。映画の答えとは違い、答えは10個あります。ウィルは8個しか答えられませんでした。ウィル・ハンティングに匹敵するか、あるいはウィルを上回れるか、試してみてください。

[ネタバレ]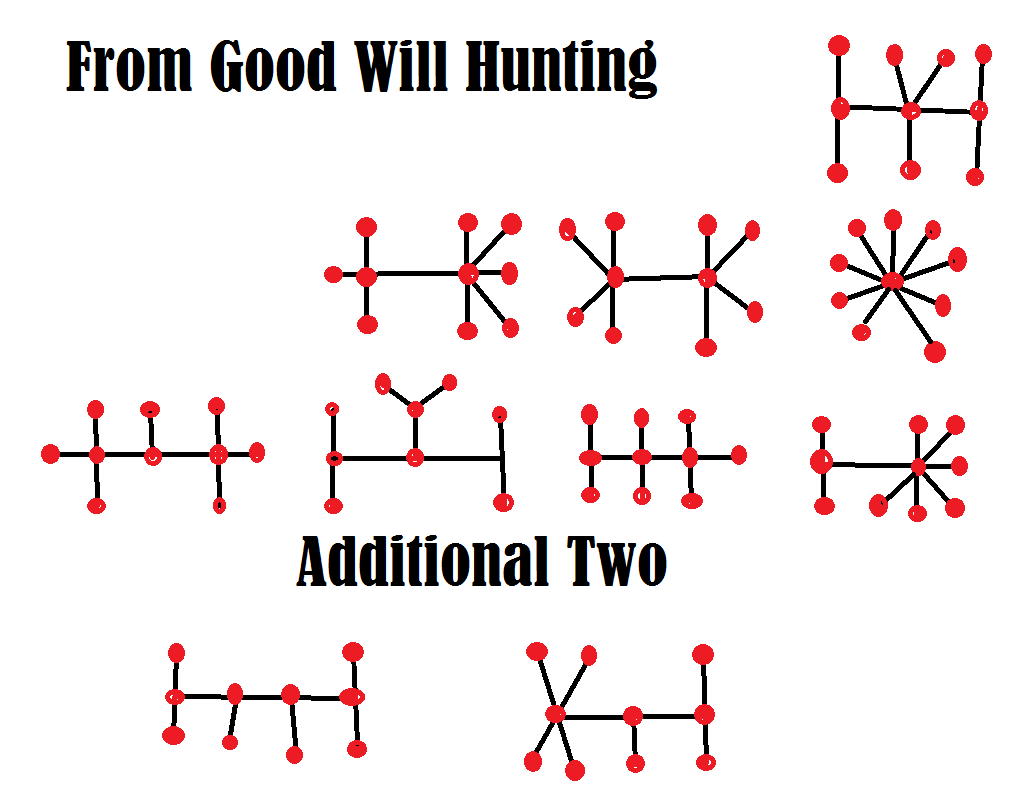

10 個すべてを導き出すための私の論理は、私のMathProblems.infoサイトの問題 220 で示されています。

[/spoiler] さらに読む:



次のルールを持つゲームを考えてみましょう。

  • 乱数ジェネレーターは、均一に分布した 0 から 1 までの乱数を提供します。
  • 2人のプレイヤーはそれぞれ別の番号を持ちます。各プレイヤーは自分の番号だけを見ることができます。
  • プレイヤー 1 は、最初の数字をそのままにするか、新しいランダムな数字と交換することができます。
  • プレイヤー 2 はプレイヤー 1 の行動を知っているため、元の番号を保持するか、新しい番号と交換するかという同じオプションがあります。
  • より高い数字を出したプレイヤーが勝ちます。

ゲームについて4つの質問があります。

  1. ゲームに関する次の質問に答えてください。
  2. プレイヤー 1 が立ち上がったり切り替えたりすることに無関心になる番号は何ですか?
  3. プレイヤー 1 がスイッチすると仮定した場合、プレイヤー 2 はどの番号で立ち上がってスイッチすることに無関心になるべきでしょうか?
  4. プレイヤー 1 がスタンドすると仮定した場合、プレイヤー 2 はどの番号でスタンドしても切り替えてもかまわないでしょうか。
  5. 両方のプレイヤーが最適な戦略をとったと仮定した場合、プレイヤー 1 が勝つ確率はどれくらいでしょうか?

匿名

答えと解答は私の数学問題のページ、問題 225 にあります。

2018年の「デッドプール」に参加します。ルールは以下のとおりです。

  1. 各プレイヤーは、100歳未満の存命の著名人10人のリストを提出しなければなりません。
  2. 2018年にAP通信の報道で明らかになったように有名人が亡くなった場合、その有名人の名前がリストに載っている人は100-xポイントを受け取る。xは死亡時の年齢。
  3. 2019 年 1 月 1 日に最も多くのポイントを獲得したプレイヤーが勝利します。

平均から考えると、このゲームに最適な戦略は何でしょうか?

匿名

元アクチュアリーとして、適切な方に質問していただきました。アクチュアリー協会が私の回答を職業上の濫用と捉えないよう願っております。とはいえ、ご質問にお答えするために、以前勤務していた社会保障局の首席アクチュアリー室の2014年生命表を参照しました。

期間生命表には、2014 年における任意の年齢および性別の人の死亡確率などが示されています。その情報を使用して、0 から 100 までのすべての年齢および性別の死亡確率と期待ポイントの両方を示す次の表を作成しました。

2014年期間生命表死亡プール

年確率
死亡 — 男性		確率
死 — 女性		期待される
ポイント — 男性		期待される
ポイント — 女性
0 0.006320 0.005310 0.632000 0.531000
1 0.000403 0.000352 0.039852 0.034835
2 0.000282 0.000221 0.027626 0.021683
3 0.000211 0.000161 0.020514 0.015612
4 0.000181 0.000131 0.017405 0.012556
5 0.000161 0.000111 0.015313 0.010515
6 0.000141 0.000111 0.013260 0.010405
7 0.000131 0.000101 0.012184 0.009360
8 0.000121 0.000091 0.011127 0.008334
9 0.000091 0.000081 0.008256 0.007328
10 0.000101 0.000091 0.009073 0.008154
11 0.000101 0.000081 0.008973 0.007168
12 0.000131 0.000101 0.011535 0.008861
13 0.000202 0.000131 0.017547 0.011389
14 0.000303 0.000151 0.026023 0.012992
15 0.000404 0.000191 0.034304 0.016267
16 0.000505 0.000232 0.042393 0.019464
17 0.000616 0.000272 0.051129 0.022582
18 0.000748 0.000302 0.061316 0.024796
19 0.000880 0.000343 0.071262 0.027768
20 0.001022 0.000373 0.081780 0.029855
21 0.001145 0.000404 0.090445 0.031884
22 0.001258 0.000444 0.098105 0.034643
23 0.001310 0.000475 0.100880 0.036546
24 0.001332 0.000495 0.101246 0.037625
25 0.001344 0.000526 0.100811 0.039422
26 0.001377 0.000556 0.101864 0.041162
27 0.001389 0.000577 0.101371 0.042106
28 0.001421 0.000608 0.102330 0.043740
29 0.001454 0.000648 0.103234 0.046036
30 0.001507 0.000669 0.105517 0.046837
31 0.001530 0.000710 0.105584 0.048998
32 0.001574 0.000751 0.107011 0.051084
33 0.001617 0.000813 0.108364 0.054454
34 0.001661 0.000864 0.109644 0.057041
35 0.001716 0.000926 0.111521 0.060194
36 0.001781 0。001008 0.113970 0.064538
37 0.001857 0.001081 0.116963 0.068090
38 0.001933 0.001164 0.119830 0.072145
39 0.002020 0.001237 0.123207 0.075427
40 0.002118 0.001340 0.127066 0.080422
41 0.002258 0.001445 0.133232 0.085232
42 0.002410 0.001560 0.139778 0.090455
43 0.002615 0.001696 0.149075 0.096649
44 0.002843 0.001853 0.159228 0.103761
45 0.003105 0.002011 0.170771 0.110606
46 0.003401 0.002191 0.183635 0.118300
47 0.003742 0.002403 0.198314 0.127342
48 0.004108 0.002647 0.213613 0.137656
49 0.004532 0.002894 0.231133 0.147577
50 0.004994 0.003194 0.249696 0.159718
51 0.005473 0.003487 0.268191 0.170880
52 0.005993 0.003794 0.287656 0.182103
53 0.006565 0.004104 0.308561 0.192871
54 0.007159 0.004428 0.329324 0.203676
55 0.007799 0.004767 0.350946 0.214498
56 0.008475 0.005153 0.372902 0.226729
57 0.009179 0.005534 0.394696 0.237972
58 0.009856 0.005889 0.413944 0.247347
59 0.010575 0.006272 0.433558 0.257150
60 0.011350 0.006683 0.453991 0.267338
61 0.012209 0.007180 0.476135 0.280016
62 0.013061 0.007720 0.496330 0.293355
63 0.013921 0.008339 0.515084 0.308537
64 0.014814 0.009029 0.533320 0.325041
65 0.015831 0.009839 0.554094 0.344371
66 0.016981 0.010741 0.577354 0.365197
67 0.018300 0.011752 0.603909 0.387812
68 0.019778 0.012879 0.632894 0.412117
69 0.021443 0.014142 0.664734 0.438397
70 0.023384 0.015613 0.701513 0.468376
71 0.025547 0.017271 0.740873 0.500852
72 0.027877 0.019047 0.780560 0.533320
73 0.030384 0.020918 0.820374 0.564797
74 0.033098 0.022938 0.860535 0.596385
75 0.036256 0.025299 0.906400 0.632465
76 0.039868 0.028043 0.956841 0.673035
77 0.043883 0.031127 1.009299 0.715914
78 0.048257 0.034590 1.061657 0.760984
79 0.053128 0.038456 1.115692 0.807583
80 0.058709 0.043007 1.174177 0.860145
81 0.065070 0.048186 1.236322 0.915536
82 0.072149 0.053762 1.298691 0.967712
83 0.079906 0.059769 1.358409 1.016065
84 0.088524 0.066380 1.416378 1.062085
85 0.098157 0。073823 1.472348 1.107351
86 0.108904 0.082381 1.524651 1.153334
87 0.120889 0.092180 1.571556 1.198344
88 0.134134 0.103305 1.609607 1.239664
89 0.148707 0.115744 1.635778 1.273180
90 0.164522 0.129477 1.645220 1.294772
91 0.181584 0.144435 1.634254 1.299911
92 0.199903 0.160621 1.599225 1.284970
93 0.219362 0.177816 1.535534 1.244713
94 0.239881 0.196194 1.439286 1.177165
95 0.260293 0.214694 1.301463 1.073469
96 0.280129 0.233056 1.120515 0.932225
97 0.299042 0.251152 0.897125 0.753456
98 0.316317 0.268235 0.632634 0.536471
99 0.332667 0.284442 0.332667 0.284442
100 0.348651 0.301417 0.000000 0.000000

表は、90 歳の男性の最大予想ポイントが 1.645220 であることを示しています。

この質問は、私のギャンブル以外のフォーラム「Diversity Tomorrow」で提起され、議論されています。

355 ミリリットルを缶に詰める場合、表面積を最小限に抑えるには寸法はどのくらいにすればよいでしょうか?

匿名

いい質問ですね！ゲームショーで細長いソーダ缶を見て、ちょうど同じ疑問を抱いていたんです。標準サイズと同じ355ミリリットルの容量だったんです。どっちも間違ってるはずがないですよね（シャーリーって呼ばないでね）。[ネタバレ] では：
r = 缶の半径
h = 缶の高さ
v = 缶の容積
s = 缶の表面積

簡単な幾何学から、表面積 = 2*pi*r^2 + 2*pi*r*h であることが分かります。

同様に、体積は pi*r^2*h であり、355 であることが分かっています。

つまり、355=pi*r^2*h です。

これを次のように並べ替えてみましょう。

(1) h = 355/(π*r^2)

私たちは知っています:

(2) s = 2*pi*r^2 + 2*pi*r*h.

式(1)のhの表現を式(2)に代入して、これを1変数の関数にしてみましょう。

s = 2*pi*r^2 + + 2*pi*r*(355/(pi*r^2))) = 2*pi*r^2 + 710/r。

最適な r を求めるために、 s の導関数をゼロに設定してみましょう。

ds/dr = 4*pi*r - 710/(r^2 ) = 0

4*π*r = 710/(r^2)

両辺にr^2を掛けると：

4*π*r^3 = 710

r^3 = 177.5/πです。

r = (177.5/pi)^(1/3) = 3.837215248。

この値を式（1）に代入するとh = 7.674430496となります。[/spoiler]

2つの缶 -- 回転

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。

私の知るギャンブルのプロのほとんどは、ゲームのボラティリティを標準偏差ではなく分散で表すことを好むようです。もちろん、前者は後者の二乗に過ぎませんが、私は賭け金や勝敗と同じ単位である標準偏差の方が好きです。おそらく、彼らは大きなボラティリティを目立たせるために、より大きな数字を好むのでしょう。あなたの見解は？ギャンブラーは「分散」を使うことを好むのでしょうか？もしそうなら、その理由は何でしょうか？

Gary J. Koehler

ゲームの標準偏差よりも変動性の方がよく話題に上がるのは同意します。私もいつも少しイライラしています。ギャンブラーがゲームのボラティリティを気にするべきだと考える理由は、勝ち負けをプレイセッションの確率と関連付ける必要があるからです。例えば、ブラックジャックを200ハンドプレイした後、1%の負けはどれくらいになるでしょうか？その答えを見つけるには、ブラックジャックの標準偏差を使うことになります。これはルールにもよりますが、約1.15です。

この質問への具体的な答えは、1.15 × 200^0.5 × -2.32635（ガウス曲線上の1%の点）= 期待値より-37.83ユニット低いということになります。ハウスエッジがあるため、損失が出る可能性があることを忘れないでください。ハウスエッジを0.3%と仮定すると、200ハンドプレイ後、0.003×200 = 0.6ハンドの損失が予想されます。つまり、1%の損失は0.6 + 37.83 = 38.43ハンドになります。

アメリカでは一般的に50%と言われている結婚が離婚に終わる確率は、離婚件数と同時期の結婚件数で計算されていると聞きました。これは本当ですか？この統計の算出方法は妥当だと思いますか？短期間の離婚と長期間の結婚を比較している点に疑問を感じます。

Gialmere

人口と年齢の分布が安定しており、離婚確率が本当に 50% であれば、サンプル数が大きい場合、一定期間内に 2 組の結婚に対して 1 組の離婚が見られることが予想されます。

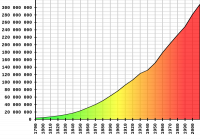
しかし、人口は安定していません。このグラフを見ると、米国の人口は10年ごとに10.71%増加していることがわかります。つまり、年間1.02%です。ここでは単純に1%と仮定しましょう。

米国の人口

地図出典：米国国勢調査

Fatherly.comによれば、失敗した結婚の平均期間は 8 年です。

現在、離婚と結婚の比率が 1 対 2 であるとすると、ある結婚が離婚で終わる平均確率はどれくらいでしょうか。

現在見られる離婚は8年前の結婚によるもので、当時の人口は現在の92.35%でした。単純計算で、実際の離婚確率は54.14%と推定されます。

確認してみましょう。

まず、CDCによると、人口1000人あたり年間6.9組の結婚があるそうです。この数字は今回の質問とは関係ありませんが、関係する数字を理解するのに役立つと思います。

8年前の人口が3億人だったと仮定すると、その年の結婚数は0.69% × 3億 = 207万件となります。

そのうちの 54.14% が 8 年後に離婚に終わるとすると、現在では 2,070,000 * 54.14% = 1,120,698 件の離婚が起こっていることになります。

1,120,698 / 2,070,000 = 現在観測されている結婚数に対する離婚数の比率は 50% です。

誰かに言われないように言っておきますが、すべての離婚がちょうど8年で終わるわけではないことは承知しています。しかし、あらゆることを考慮すると、最終的な離婚率は私の推定する54.14%とそれほど変わらないでしょう。

この質問は、 Wizard of Vegasの私のフォーラムで提起され、議論されています。

100人の従業員がいるオフィスで、シークレットサンタのプレゼント交換をします。全員の名前を紙に書いて帽子に入れ、全員でランダムに名前を引いてプレゼントを贈ります。

問題は、平均していくつの閉じたループが存在するかということです。例えば、ゴードンがドンに渡し、ドンがジョンに渡し、ジョンがネイサンに渡し、ネイサンがゴードンに渡す、といった閉じたループです。あるいは、自分で名前を引く、といった具合です。

匿名

全員が一度に一つずつ選択することを考えてみましょう。一人ずつ選択していくと、以下の2つの状況が発生します。

  1. 選ぶ人の名前はすでに選ばれています。
  2. 選んだ人の名前はまだ名前の箱の中に残っています。

任意の選択者に対して、選択する人が n 人残っているとします。

選んだ人の名前が既に選ばれている場合、選んだ人が自分の名前を含むループを閉じる確率は1/nです。例えば、エイミーが選んだとします。エイミーの名前は既にボブが、ボブの名前は既にチャーリーが選んでおり、チャーリーの名前はまだビンに残っています。ビンにまだn個の名前が残っている場合、エイミーがチャーリーの名前を選び、ループを閉じる確率は1/nです。

選んだ人の名前がまだ選ばれていない場合、エイミーが自分の名前を選ぶ確率は 1/n で、ループが閉じます。

いずれにせよ、ピッカーがループを閉じない場合、別のチェーンの一部に加わることになり、そのチェーンは最終的に他の誰かによって閉じられます。各チェーンは、閉じられた時点で一度だけカウントされます。

したがって答えは 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518 です。

十分に大きなプレイヤー数 n の場合の推定値は ln(n) です。

この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

ウィザードに質問コラム #314 を記念して、合計が円周率の関数になるお気に入りの無限級数は何ですか?

Heather

おそらく最も有名なのは次の 2 つなので、簡単に選択できます。

  • 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
  • 1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 + ... = π^2/6

23人をランダムに選んだ場合、2人以上の人が少なくとも1人の誕生日が一致する確率は50%以上だと聞いたことがあります。これは本当ですか？他の人数のグループで誕生日が一致する確率はどれくらいですか？3人、4人、5人の場合でも同じ質問です。

匿名

確かに、ランダムに選んだ23人のうち、少なくとも1組が共通の誕生日を持つ確率は50.73%です。これは閏日を無視し、全員が他の365日に生まれる確率が等しいと仮定した場合の計算です（実際にはそうではなく、春と秋の誕生日の方がわずかに多いです）。

ご質問への回答の表は長すぎるため、ネタバレタグを付けさせていただきます。回答をご覧になるにはボタンをクリックしてください。

2人以上の共通の誕生日

グループサイズ確率
2 0.002740
3 0.008204
4 0.016356
5 0.027136
6 0.040462
7 0.056236
8 0.074335
9 0.094624
10 0.116948
11 0.141141
12 0.167025
13 0.194410
14 0.223103
15 0.252901
16 0.283604
17 0.315008
18 0.346911
19 0.379119
20 0.411438
21 0.443688
22 0.475695
23 0.507297
24 0.538344
25 0.568700
26 0.598241
27 0.626859
28 0.654461
29 0.680969
30 0.706316
31 0.730455
32 0.753348
33 0.774972
34 0.795317
35 0.814383
36 0.832182
37 0.848734
38 0.864068
39 0.878220
40 0.891232
41 0.903152
42 0.914030
43 0.923923
44 0.932885
45 0.940976
46 0.948253
47 0.954774
48 0.960598
49 0.965780
50 0.970374
51 0.974432
52 0.978005
53 0.981138
54 0.983877
55 0.986262
56 0.988332
57 0.990122
58 0.991665
59 0.992989
60 0.994123
61 0.995089
62 0.995910
63 0.996604
64 0.997190
65 0.997683
66 0.998096
67 0.998440
68 0.998726
69 0.998964
70 0.999160
71 0.999321
72 0.999453
73 0.999561
74 0.999649
75 0.999720
76 0.999777
77 0.999824
78 0.999861
79 0.999891
80 0.999914
81 0.999933
82 0.999948
83 0.999960
84 0.999969

3人以上の共通の誕生日

グループサイズ確率
3 0.000008
4 0.000030
5 0.000075
6 0.000149
7 0.000261
8 0.000416
9 0.000623
10 0.000888
11 0.001218
12 0.001621
13 0.002102
14 0.002670
15 0.003329
16 0.004088
17 0.004953
18 0.005929
19 0.007024
20 0.008243
21 0.009592
22 0.011078
23 0.012705
24 0.014481
25 0.016409
26 0.018497
27 0.020747
28 0.023167
29 0.025760
30 0.028531
31 0.031484
32 0.034624
33 0.037954
34 0.041479
35 0.045202
36 0.049126
37 0.053254
38 0.057589
39 0.062133
40 0.066889
41 0.071859
42 0.077044
43 0.082446
44 0.088065
45 0.093903
46 0.099960
47 0.106236
48 0.112731
49 0.119444
50 0.126375
51 0.133522
52 0.140885
53 0.148460
54 0.156246
55 0.164241
56 0.172441
57 0.180844
58 0.189445
59 0.198242
60 0.207230
61 0.216405
62 0.225761
63 0.235294
64 0.244999
65 0.254869
66 0.264899
67 0.275082
68 0.285413
69 0.295883
70 0.306487
71 0.317217
72 0.328066
73 0.339026
74 0.350088
75 0.361246
76 0.372491
77 0.383814
78 0.395207
79 0.406662
80 0.418169
81 0.429720
82 0.441307
83 0.452920
84 0.464550
85 0.476188
86 0.487826
87 0.499455
88 0.511065
89 0.522648
90 0.534196
91 0.545698
92 0.557148
93 0.568537
94 0.579855
95 0.591096
96 0.602252
97 0.613314
98 0.624275
99 0.635127
100 0.645865
101 0.656480
102 0.666967
103 0.677318
104 0。687529
105 0.697593
106 0.707505
107 0.717260
108 0.726853
109 0.736279
110 0.745536
111 0.754619
112 0.763525
113 0.772251
114 0.780795
115 0.789155
116 0.797330
117 0.805319
118 0.813121
119 0.820580
120 0.827964
121 0.835152
122 0.842144
123 0.848940
124 0.855540
125 0.861945
126 0.868155
127 0.874172
128 0.879996
129 0.885631
130 0.891076
131 0.896335
132 0.901409
133 0.906302
134 0.911015
135 0.915552
136 0.919915
137 0.924108
138 0.928135
139 0.931997
140 0.935700
141 0.939246
142 0.942640
143 0.945885
144 0.948985
145 0.951944
146 0.954766
147 0.957456
148 0.960016
149 0.962452
150 0.964767
151 0.966965
152 0.969050
153 0.971028
154 0.972900
155 0.974672
156 0.976347
157 0.977930
158 0.979423
159 0.980831
160 0.982158
161 0.983407
162 0.984581
163 0.985684
164 0.986719
165 0.987690
166 0.988600
167 0.989452
168 0.990248
169 0.990992
170 0.991687
171 0.992335
172 0.992938
173 0.993500
174 0.994022
175 0.994508
176 0.994958
177 0.995376
178 0.995763
179 0.996121
180 0.996452
181 0.996758
182 0.997040
183 0.997300
184 0.997540
185 0.997760
186 0.997963
187 0.998149
188 0.998319
189 0.998476
190 0.998619
191 0.998750
192 0.998869
193 0.998979
194 0.999078
195 0.999169
196 0.999251
197 0.999326
198 0.999394
199 0.999456
200 0.999512
201 0.999562
202 0.999608
203 0.999650
204 0.999687
205 0.999720
206 0.999751
207 0.999778
208 0.999802
209 0.999824
210 0.999844
211 0.999862
212 0.999877
213 0.999891
214 0.999904
215 0。999915
216 0.999925
217 0.999934
218 0.999942
219 0.999949
220 0.999955
221 0.999961
222 0.999966
223 0.999970
224 0.999974
225 0.999977
226 0.999980
227 0.999982
228 0.999985
229 0.999987
230 0.999988
231 0.999990
232 0.999991
233 0.999992
234 0.999994
235 0.999994
236 0.999995
237 0.999996
238 0.999996
239 0.999997
240 0.999997
241 0.999998
242 0.999998
243 0.999998
244 0.999999

4人以上の共通の誕生日

グループサイズ確率
4 0.000000
5 0.000000
6 0.000000
7 0.000001
8 0.000001
9 0.000003
10 0.000004
11 0.000007
12 0.000010
13 0.000014
14 0.000020
15 0.000027
16 0.000036
17 0.000048
18 0.000061
19 0.000077
20 0.000096
21 0.000119
22 0.000145
23 0.000175
24 0.000209
25 0.000248
26 0.000293
27 0.000343
28 0.000399
29 0.000462
30 0.000532
31 0.000610
32 0.000695
33 0.000790
34 0.000893
35 0.001006
36 0.001129
37 0.001263
38 0.001408
39 0.001566
40 0.001736
41 0.001919
42 0.002116
43 0.002328
44 0.002555
45 0.002798
46 0.003058
47 0.003334
48 0.003629
49 0.003943
50 0.004276
51 0.004629
52 0.005003
53 0.005399
54 0.005817
55 0.006258
56 0.006724
57 0.007214
58 0.007730
59 0.008272
60 0.008841
61 0.009439
62 0.010065
63 0.010721
64 0.011408
65 0.012126
66 0.012876
67 0.013659
68 0.014476
69 0.015327
70 0.016215
71 0.017139
72 0.018100
73 0.019099
74 0.020137
75 0.021215
76 0.022334
77 0.023495
78 0.024698
79 0.025944
80 0.027235
81 0.028570
82 0.029951
83 0.031379
84 0.032855
85 0.034379
86 0.035952
87 0.037575
88 0.039249
89 0.040974
90 0.042752
91 0.044583
92 0.046467
93 0.048407
94 0.050402
95 0.052453
96 0.054561
97 0.056726
98 0.058950
99 0.061233
100 0.063576
101 0.065978
102 0.068442
103 0.070967
104 0.073554
105 0。076204
106 0.078917
107 0.081694
108 0.084535
109 0.087441
110 0.090412
111 0.093449
112 0.096552
113 0.099722
114 0.102958
115 0.106262
116 0.109633
117 0.113072
118 0.116579
119 0.120154
120 0.123798
121 0.127510
122 0.131292
123 0.135142
124 0.139061
125 0.143050
126 0.147107
127 0.151234
128 0.155429
129 0.159694
130 0.164027
131 0.168429
132 0.172899
133 0.177438
134 0.182044
135 0.186719
136 0.191460
137 0.196269
138 0.201144
139 0.206085
140 0.211091
141 0.216163
142 0.221299
143 0.226499
144 0.231763
145 0.237089
146 0.242476
147 0.247925
148 0.253434
149 0.259002
150 0.264629
151 0.270314
152 0.276055
153 0.281852
154 0.287703
155 0.293608
156 0.299566
157 0.305575
158 0.311634
159 0.317741
160 0.323897
161 0.330099
162 0.336346
163 0.342637
164 0.348970
165 0.355343
166 0.361757
167 0.368208
168 0.374696
169 0.381218
170 0.387774
171 0.394362
172 0.400980
173 0.407626
174 0.414299
175 0.420997
176 0.427718
177 0.434462
178 0.441224
179 0.448005
180 0.454803
181 0.461615
182 0.468439
183 0.475274
184 0.482118
185 0.488969
186 0.495826
187 0.502685
188 0.509546
189 0.516407
190 0.523265
191 0.530119
192 0.536967
193 0.543807
194 0.550636
195 0.557454
196 0.564258
197 0.571046
198 0.577817
199 0.584568
200 0.591298
201 0.598005
202 0.604687
203 0.611342
204 0.617969
205 0.624565
206 0.631129
207 0.637659
208 0.644154
209 0.650611
210 0.657030
211 0.663407
212 0.669743
213 0.676035
214 0.682281
215 0.688481
216 0。694632
217 0.700734
218 0.706784
219 0.712782
220 0.718726
221 0.724614
222 0.730446
223 0.736220
224 0.741936
225 0.747591
226 0.753185
227 0.758717
228 0.764185
229 0.769590
230 0.774929
231 0.780202
232 0.785409
233 0.790547
234 0.795618
235 0.800619
236 0.805551
237 0.810412
238 0.815202
239 0.819921
240 0.824569
241 0.829144
242 0.833646
243 0.838076
244 0.842432
245 0.846716
246 0.850925
247 0.855061
248 0.859123
249 0.863112
250 0.867027
251 0.870868
252 0.874635
253 0.878329
254 0.881950
255 0.885498
256 0.888973
257 0.892375
258 0.895705
259 0.898964
260 0.902151
261 0.905268
262 0.908314
263 0.911290
264 0.914197
265 0.917036
266 0.919806
267 0.922509
268 0.925145
269 0.927715
270 0.930220
271 0.932661
272 0.935037
273 0.937351
274 0.939603
275 0.941793
276 0.943923
277 0.945993
278 0.948005
279 0.949960
280 0.951857
281 0.953699
282 0.955486
283 0.957218
284 0.958898
285 0.960527
286 0.962104
287 0.963631
288 0.965109
289 0.966540
290 0.967923
291 0.969260
292 0.970553
293 0.971802
294 0.973007
295 0.974171
296 0.975294
297 0.976377
298 0.977421
299 0.978427
300 0.979397
301 0.980330
302 0.981228
303 0.982092
304 0.982923
305 0.983722
306 0.984490
307 0.985227
308 0.985935
309 0.986614
310 0.987266
311 0.987890
312 0.988489
313 0.989063
314 0.989612
315 0.990138
316 0.990641
317 0.991122
318 0.991581
319 0.992021
320 0.992440
321 0.992841
322 0.993223
323 0.993587
324 0.993935
325 0.994266
326 0.994581
327 0。994882
328 0.995167
329 0.995439
330 0.995698
331 0.995943
332 0.996176
333 0.996398
334 0.996608
335 0.996807
336 0.996996
337 0.997175
338 0.997344
339 0.997505
340 0.997657
341 0.997801
342 0.997936
343 0.998065
344 0.998186
345 0.998300
346 0.998408
347 0.998510
348 0.998606
349 0.998696
350 0.998781
351 0.998861
352 0.998937
353 0.999008
354 0.999074
355 0.999137
356 0.999195
357 0.999250
358 0.999302
359 0.999350
360 0.999396
361 0.999438
362 0.999478
363 0.999515
364 0.999550
365 0.999582
366 0.999613
367 0.999641
368 0.999668
369 0.999692
370 0.999715
371 0.999736
372 0.999756
373 0.999775
374 0.999792
375 0.999808
376 0.999823
377 0.999837
378 0.999850
379 0.999861
380 0.999872
381 0.999883
382 0.999892
383 0.999901
384 0.999909
385 0.999916
386 0.999923
387 0.999930
388 0.999935
389 0.999941
390 0.999946
391 0.999950
392 0.999955
393 0.999959
394 0.999962
395 0.999965
396 0.999969
397 0.999971
398 0.999974
399 0.999976
400 0.999978
401 0.999980
402 0.999982
403 0.999984
404 0.999985
405 0.999987
406 0.999988
407 0.999989
408 0.999990
409 0.999991
410 0.999992
411 0.999993
412 0.999993
413 0.999994
414 0.999995
415 0.999995
416 0.999996
417 0.999996
418 0.999996
419 0.999997
420 0.999997
421 0.999997
422 0.999998
423 0.999998
424 0.999998
425 0.999998
426 0.999998
427 0.999999
428 0.999999
429 0.999999

5人以上の共通の誕生日

グループサイズ確率
5 0.000000
6 0.000000
7 0.000000
8 0.000000
9 0.000000
10 0.000000
11 0.000000
12 0.000000
13 0.000000
14 0.000000
15 0.000000
16 0.000000
17 0.000000
18 0.000001
19 0.000001
20 0.000001
21 0.000001
22 0.000002
23 0.000002
24 0.000003
25 0.000004
26 0.000004
27 0.000005
28 0.000006
29 0.000008
30 0.000009
31 0.000011
32 0.000013
33 0.000015
34 0.000017
35 0.000020
36 0.000023
37 0.000026
38 0.000030
39 0.000034
40 0.000039
41 0.000044
42 0.000050
43 0.000056
44 0.000063
45 0.000070
46 0.000079
47 0.000087
48 0.000097
49 0.000108
50 0.000119
51 0.000132
52 0.000145
53 0.000159
54 0.000175
55 0.000192
56 0.000209
57 0.000229
58 0.000249
59 0.000271
60 0.000295
61 0.000320
62 0.000347
63 0.000375
64 0.000406
65 0.000438
66 0.000472
67 0.000509
68 0.000547
69 0.000588
70 0.000631
71 0.000676
72 0.000725
73 0.000775
74 0.000829
75 0.000885
76 0.000944
77 0.001007
78 0.001072
79 0.001141
80 0.001213
81 0.001289
82 0.001369
83 0.001452
84 0.001539
85 0.001630
86 0.001726
87 0.001825
88 0.001930
89 0.002038
90 0.002152
91 0.002270
92 0.002394
93 0.002522
94 0.002656
95 0.002796
96 0.002941
97 0.003092
98 0.003249
99 0.003412
100 0.003581
101 0.003757
102 0.003939
103 0.004128
104 0.004325
105 0.004528
106 0。004739
107 0.004957
108 0.005183
109 0.005417
110 0.005659
111 0.005909
112 0.006168
113 0.006436
114 0.006712
115 0.006998
116 0.007293
117 0.007597
118 0.007912
119 0.008236
120 0.008570
121 0.008915
122 0.009270
123 0.009636
124 0.010013
125 0.010402
126 0.010801
127 0.011213
128 0.011637
129 0.012072
130 0.012521
131 0.012981
132 0.013455
133 0.013942
134 0.014442
135 0.014956
136 0.015484
137 0.016026
138 0.016582
139 0.017153
140 0.017739
141 0.018340
142 0.018956
143 0.019588
144 0.020235
145 0.020899
146 0.021580
147 0.022277
148 0.022991
149 0.023722
150 0.024470
151 0.025237
152 0.026021
153 0.026824
154 0.027645
155 0.028485
156 0.029344
157 0.030222
158 0.031120
159 0.032037
160 0.032975
161 0.033934
162 0.034913
163 0.035912
164 0.036934
165 0.037976
166 0.039040
167 0.040127
168 0.041235
169 0.042367
170 0.043521
171 0.044698
172 0.045898
173 0.047122
174 0.048370
175 0.049642
176 0.050939
177 0.052260
178 0.053606
179 0.054977
180 0.056374
181 0.057796
182 0.059245
183 0.060719
184 0.062220
185 0.063748
186 0.065302
187 0.066884
188 0.068493
189 0.070130
190 0.071795
191 0.073487
192 0.075209
193 0.076958
194 0.078737
195 0.080544
196 0.082381
197 0.084247
198 0.086143
199 0.088068
200 0.090024
201 0.092009
202 0.094026
203 0.096072
204 0.098150
205 0.100259
206 0.102398
207 0.104569
208 0.106772
209 0.109006
210 0.111272
211 0.113570
212 0.115899
213 0.118262
214 0.120656
215 0.123083
216 0.125542
217 0。128035
218 0.130559
219 0.133117
220 0.135708
221 0.138332
222 0.140989
223 0.143679
224 0.146403
225 0.149160
226 0.151950
227 0.154774
228 0.157632
229 0.160522
230 0.163447
231 0.166405
232 0.169396
233 0.172421
234 0.175480
235 0.178572
236 0.181698
237 0.184857
238 0.188049
239 0.191275
240 0.194534
241 0.197827
242 0.201152
243 0.204511
244 0.207902
245 0.211327
246 0.214784
247 0.218274
248 0.221796
249 0.225351
250 0.228937
251 0.232556
252 0.236207
253 0.239889
254 0.243603
255 0.247348
256 0.251124
257 0.254931
258 0.258768
259 0.262636
260 0.266534
261 0.270462
262 0.274419
263 0.278406
264 0.282422
265 0.286466
266 0.290539
267 0.294639
268 0.298768
269 0.302924
270 0.307106
271 0.311316
272 0.315551
273 0.319813
274 0.324100
275 0.328412
276 0.332749
277 0.337110
278 0.341495
279 0.345903
280 0.350334
281 0.354788
282 0.359264
283 0.363761
284 0.368279
285 0.372818
286 0.377376
287 0.381955
288 0.386552
289 0.391167
290 0.395801
291 0.400452
292 0.405119
293 0.409803
294 0.414503
295 0.419217
296 0.423946
297 0.428689
298 0.433445
299 0.438214
300 0.442995
301 0.447787
302 0.452590
303 0.457403
304 0.462226
305 0.467057
306 0.471897
307 0.476744
308 0.481599
309 0.486459
310 0.491325
311 0.496196
312 0.501070
313 0.505949
314 0.510830
315 0.515713
316 0.520598
317 0.525483
318 0.530369
319 0.535253
320 0.540137
321 0.545018
322 0.549896
323 0.554771
324 0.559642
325 0.564507
326 0.569367
327 0.574221
328 0。579067
329 0.583906
330 0.588736
331 0.593557
332 0.598368
333 0.603169
334 0.607958
335 0.612735
336 0.617500
337 0.622251
338 0.626988
339 0.631710
340 0.636417
341 0.641107
342 0.645781
343 0.650437
344 0.655075
345 0.659695
346 0.664295
347 0.668875
348 0.673434
349 0.677972
350 0.682488
351 0.686981
352 0.691451
353 0.695897
354 0.700319
355 0.704716
356 0.709088
357 0.713433
358 0.717752
359 0.722043
360 0.726307
361 0.730543
362 0.734750
363 0.738927
364 0.743075
365 0.747193
366 0.751279
367 0.755335
368 0.759359
369 0.763351
370 0.767310
371 0.771237
372 0.775130
373 0.778990
374 0.782815
375 0.786606
376 0.790363
377 0.794084
378 0.797770
379 0.801420
380 0.805034
381 0.808611
382 0.812152
383 0.815656
384 0.819123
385 0.822553
386 0.825945
387 0.829300
388 0.832616
389 0.835895
390 0.839135
391 0.842336
392 0.845499
393 0.848624
394 0.851709
395 0.854756
396 0.857764
397 0.860733
398 0.863663
399 0.866553
400 0.869405
401 0.872217
402 0.874990
403 0.877724
404 0.880419
405 0.883075
406 0.885692
407 0.888269
408 0.890808
409 0.893309
410 0.895770
411 0.898193
412 0.900578
413 0.902924
414 0.905232
415 0.907502
416 0.909734
417 0.911929
418 0.914086
419 0.916205
420 0.918288
421 0.920334
422 0.922344
423 0.924317
424 0.926254
425 0.928155
426 0.930020
427 0.931851
428 0.933646
429 0.935406
430 0.937133
431 0.938825
432 0.940483
433 0.942108
434 0.943699
435 0.945258
436 0.946785
437 0.948279
438 0.949741
439 0。951173
440 0.952573
441 0.953942
442 0.955281
443 0.956590
444 0.957870
445 0.959120
446 0.960342
447 0.961535
448 0.962701
449 0.963838
450 0.964949
451 0.966032
452 0.967090
453 0.968121
454 0.969127
455 0.970107
456 0.971063
457 0.971994
458 0.972902
459 0.973785
460 0.974646
461 0.975484
462 0.976299
463 0.977093
464 0.977865
465 0.978616
466 0.979346
467 0.980056
468 0.980746
469 0.981416
470 0.982067
471 0.982699
472 0.983313
473 0.983909
474 0.984488
475 0.985049
476 0.985593
477 0.986121
478 0.986633
479 0.987128
480 0.987609
481 0.988074
482 0.988525
483 0.988962
484 0.989384
485 0.989793
486 0.990189
487 0.990571
488 0.990941
489 0.991299
490 0.991644
491 0.991978
492 0.992301
493 0.992612
494 0.992913
495 0.993203
496 0.993483
497 0.993753
498 0.994013
499 0.994264
500 0.994506
501 0.994740
502 0.994964
503 0.995180
504 0.995389
505 0.995589
506 0.995782
507 0.995967
508 0.996146
509 0.996317
510 0.996482
511 0.996640
512 0.996793
513 0.996939
514 0.997079
515 0.997213
516 0.997343
517 0.997466
518 0.997585
519 0.997699
520 0.997808
521 0.997913
522 0.998013
523 0.998109
524 0.998200
525 0.998288
526 0.998372
527 0.998452
528 0.998529
529 0.998602
530 0.998673
531 0.998739
532 0.998803
533 0.998864
534 0.998923
535 0.998978
536 0.999031
537 0.999082
538 0.999130
539 0.999176
540 0.999219
541 0.999261
542 0.999301
543 0.999338
544 0.999374
545 0.999408
546 0.999441
547 0.999471
548 0.999501
549 0.999528
550 0。999555
551 0.999580
552 0.999604
553 0.999626
554 0.999648
555 0.999668
556 0.999687
557 0.999705
558 0.999722
559 0.999739
560 0.999754
561 0.999769
562 0.999782
563 0.999795
564 0.999808
565 0.999819
566 0.999830
567 0.999841
568 0.999851
569 0.999860
570 0.999868
571 0.999877
572 0.999884
573 0.999892
574 0.999899
575 0.999905
576 0.999911
577 0.999917
578 0.999922
579 0.999927
580 0.999932
581 0.999936
582 0.999941
583 0.999945
584 0.999948
585 0.999952
586 0.999955
587 0.999958
588 0.999961
589 0.999964
590 0.999966
591 0.999968
592 0.999971
593 0.999973
594 0.999975
595 0.999976
596 0.999978
597 0.999980
598 0.999981
599 0.999982
600 0.999984
601 0.999985
602 0.999986
603 0.999987
604 0.999988
605 0.999989
606 0.999990
607 0.999990
608 0.999991
609 0.999992
610 0.999992
611 0.999993
612 0.999994
613 0.999994
614 0.999994
615 0.999995
616 0.999995
617 0.999996
618 0.999996
619 0.999996
620 0.999997
621 0.999997
622 0.999997
623 0.999997
624 0.999998
625 0.999998
626 0.999998
627 0.999998
628 0.999998
629 0.999998
630 0.999999
631 0.999999
632 0.999999
633 0.999999
634 0.999999

ディーラーが1ドルで割り切れる額面のチップを全て持っているとします。テーブルで10ドルでバイインします。ディーラーは10ドルのお釣りを何通りの方法で渡すでしょうか？他の金額ではどうでしょうか？

匿名

ディーラーが10ドルを分割する方法は42通りあります。以下に挙げます。

10
9.1
8,2
8,1,1
7,3
7,2,1
7、1、1、1
6,4
6,3,1
6,2,2
6、2、1、1
6、1、1、1、1
5.5
5,4,1
5,3,2
5、3、1、1
5、2、2、1
5、2、1、1、1
5、1、1、1、1、1
4,4,2
4、4、1、1
4,3,3
4、3、2、1
4、3、1、1、1
4、2、2、2
4、2、2、1、1
4、2、1、1、1、1
4、1、1、1、1、1、1
3、3、3、1
3、3、2、2
3、3、2、1、1
3、3、1、1、1、1
3、2、2、2、1
3、2、2、1、1、1
3、2、1、1、1、1、1
3、1、1、1、1、1、1、1
2、2、2、2、2
2、2、2、2、1、1
2、2、2、1、1、1、1
2、2、1、1、1、1、1、1
2、1、1、1、1、1、1、1、1
1,1,1,1,1,1,1,1,1,1,1

数学者はこれを分割と呼びます。ここでは、私のコンピュータで計算できる最大値（2の64乗）である405までの初期値に対する分割数を示します。

2人以上の共通の誕生日

<!--/ボックスタイトル-->
>241
イニシャル
量		合計
パーティション
1 1
2 2
3 3
4 5
5 7
6 11
7 15
8 22
9 30
10 42
11 56
12 77
13 101
14 135
15 176
16 231
17 297
18 385
19 490
20 627
21 792
22 1002
23 1255
24 1575
25 1958
26 2436
27 3010
28 3718
29 4565
30 5604
31 6842
32 8349
33 10143
34 12310
35 14883
36 17977
37 21637
38 26015
39 31185
40 37338
41 44583
42 53174
43 63261
44 75175
45 89134
46 105558
47 124754
48 147273
49 173525
50 204226
51 239943
52 281589
53 329931
54 386155
55 451276
56 526823
57 614154
58 715220
59 831820
60 966467
61 1121505
62 1300156
63 1505499
64 1741630
65 2012558
66 2323520
67 2679689
68 3087735
69 3554345
70 4087968
71 4697205
72 5392783
73 6185689
74 7089500
75 8118264
76 9289091
77 10619863
78 12132164
79 13848650
80 15796476
81 18004327
82 20506255
83 23338469
84 26543660
85 30167357
86 34262962
87 38887673
88 44108109
89 49995925
90 56634173
91 64112359
92 72533807
93 82010177
94 92669720
95 104651419
96 118114304
97 133230930
98 150198136
99 169229875
100 190569292
101 214481126
102 241265379
103 271248950
104 304801365
105 342325709
106 384276336
107 431149389
108 483502844
109 541946240
110 607163746
111 679903203
112 761002156
113 851376628
114 952050665
115 1064144451
116 1188908248
117 1327710076
118 1482074143
119 1653668665
120 1844349560
121 2056148051
122 2291320912
123 2552338241
124 2841940500
125 3163127352
126 3519222692
127 3913864295
128 4351078600
129 4835271870
130 5371315400
131 5964539504
132 6620830889
133 7346629512
134 8149040695
135 9035836076
136 10015581680
137 11097645016
138 12292341831
139 13610949895
140 15065878135
141 16670689208
142 18440293320
143 20390982757
144 22540654445
145 24908858009
146 27517052599
147 30388671978
148 33549419497
149 37027355200
150 40853235313
151 45060624582
152 49686288421
153 54770336324
154 60356673280
155 66493182097
156 73232243759
157 80630964769
158 88751778802
159 97662728555
160 107438159466
161 118159068427
162 129913904637
163 142798995930
164 156919475295
165 172389800255
166 189334822579
167 207890420102
168 228204732751
169 250438925115
170 274768617130
171 301384802048
172 330495499613
173 362326859895
174 397125074750
175 435157697830
176 476715857290
177 522115831195
178 571701605655
179 625846753120
180 684957390936
181 749474411781
182 819876908323
183 896684817527
184 980462880430
185 1071823774337
186 1171432692373
187 1280011042268
188 1398341745571
189 1527273599625
190 1667727404093
191 1820701100652
192 1987276856363
193 2168627105469
194 2366022741845
195 2580840212973
196 2814570987591
197 3068829878530
198 3345365983698
199 3646072432125
200 3972999029388
201 4328363658647
202 4714566886083
203 5134205287973
204 5590088317495
205 6085253859260
206 6622987708040
207 7206841706490
208 7840656226137
209 8528581302375
210 9275102575355
211 10085065885767
212 10963707205259
213 11916681236278
214 12950095925895
215 14070545699287
216 15285151248481
217 16601598107914
218 18028182516671
219 19573856161145
220 21248279009367
221 23061871173849
222 25025873760111
223 27152408925615
224 29454549941750
225 31946390696157
226 34643126322519
227 37561133582570
228 40718063627362
229 44132934884255
230 47826239745920
231 51820051838712
232 56138148670947
233 60806135438329
234 65851585970275
235 71304185514919
236 77195892663512
237 83561103925871
238 90436839668817
239 97862933703585
240 105882246722733
114540884553038
242 123888443077259
243 133978259344888
244 144867692496445
245 156618412527946
246 169296722391554
247 182973889854026
248 197726516681672
249 213636919820625
250 230793554364681
251 249291451168559
252 269232701252579
253 290726957916112
254 313891991306665
255 338854264248680
256 365749566870782
257 394723676655357
258 425933084409356
259 459545750448675
260 495741934760846
261 534715062908609
262 576672674947168
263 621837416509615
264 670448123060170
265 722760953690372
266 779050629562167
267 839611730366814
268 904760108316360
269 974834369944625
270 1050197489931117
271 1131238503938606
272 1218374349844333
273 1312051800816215
274 1412749565173450
275 1520980492851175
276 1637293969337171
277 1762278433057269
278 1896564103591584
279 2040825852575075
280 2195786311682516
281 2362219145337711
282 2540952590045698
283 2732873183547535
284 2938929793929555
285 3160137867148997
286 3397584011986773
287 3652430836071053
288 3925922161489422
289 4219388528587095
290 4534253126900886
291 4872038056472084
292 5234371069753672
293 5622992691950605
294 6039763882095515
295 6486674127079088
296 6965850144195831
297 7479565078510584
298 8030248384943040
299 8620496275465025
300 9253082936723602
301 9930972392403501
302 10657331232548839
303 11435542077822104
304 12269218019229465
305 13162217895057704
306 14118662665280005
307 15142952738857194
308 16239786535829663
309 17414180133147295
310 18671488299600364
311 20017426762576945
312 21458096037352891
313 23000006655487337
314 24650106150830490
315 26415807633566326
316 28305020340996003
317 30326181989842964
318 32488293351466654
319 34800954869440830
320 37274405776748077
321 39919565526999991
322 42748078035954696
323 45772358543578028
324 49005643635237875
325 52462044228828641
326 56156602112874289
327 60105349839666544
328 64325374609114550
329 68834885946073850
330 73653287861850339
331 78801255302666615
332 84300815636225119
333 90175434980549623
334 96450110192202760
335 103151466321735325
336 110307860425292772
337 117949491546113972
338 126108517833796355
339 134819180623301520
340 144117936527873832
341 154043597379576030
342 164637479165761044d>
343 175943559810422753
344 188008647052292980
345 200882556287683159
346 214618299743286299
347 229272286871217150
348 244904537455382406
349 261578907351144125
350 279363328483702152
351 298330063062758076
352 318555973788329084
353 340122810048577428
354 363117512048110005
355 387632532919029223
356 413766180933342362
357 441622981929358437
358 471314064268398780
359 502957566506000020
360 536679070310691121
361 572612058898037559
362 610898403751884101
363 651688879997206959
364 695143713458946040
365 741433159884081684
366 790738119649411319
367 843250788562528427
368 899175348396088349
369 958728697912338045
370 1022141228367345362
371 1089657644424399782
372 1161537834849962850
373 1238057794119125085
374 1319510599727473500
375 1406207446561484054
376 1498478743590581081
377 1596675274490756791
378 1701169427975813525
379 1812356499739472950
380 1930656072350465812
381 2056513475336633805
382 2190401332423765131
383 2332821198543892336
384 2484305294265418180
385 2645418340688763701
386 2816759503217942792
387 2998964447736452194
388 3192707518433532826
389 3398704041358160275
390 3617712763867604423
391 3850538434667429186
392 4098034535626594791
393 4361106170762284114
394 4640713124699623515
395 4937873096788191655
396 5253665124416975163
397 5589233202595404488
398 5945790114707874597
399 6324621482504294325
400 6727090051741041926
401 7154640222653942321
402 7608802843339879269
403 8091200276484465581
404 8603551759348655060
405 9147679068859117602

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。

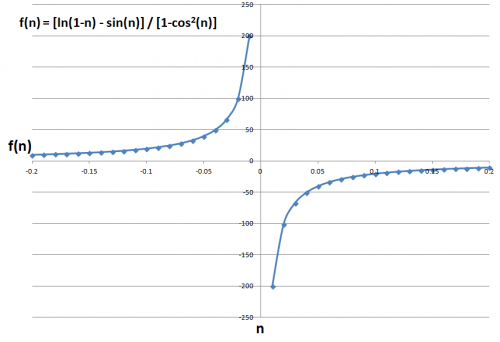
映画「ミーン・ガールズ」で問われているように、次の質問とは何ですか?

匿名

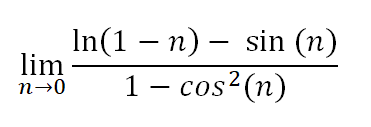
まず、n (x 軸) と f(n) (y 軸) のグラフを見てみましょう。

意地悪な女の子のグラフ

ご覧の通り、極限は左から∞、右から-∞に近づいていきます。左右から同じ場所には向かないので、極限は存在しません。

しかし、グラフを描かずに質問に答えてみましょう。ロピタルの定理によれば、f(x)/g(x) の極限が 0/0 のとき、lim f(x)/g(x) = lim f'(x)/g'(x) となります。そこで、f'(x) と g'(x) を解きましょう。

f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn

積の法則を使って sin 2 (n) d/dn を解いてみましょう。

sin 2 (n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n)。

次に、n = 0 で f'(n) と g'(n) を解きます。

f'(0) = -1/(1-0) - cos(0) = -2 です。
g'(0) = 2sin(0)cos(0) = 0

したがって、f'(0)/g'(0) = -2/0 = -∞ となります。したがって、元の関数の極限は存在しません。

『ミーン・ガールズ』の脚本家たちがこの映画の数学を完璧に描き出したことに賛辞を送りたい。『グッド・ウィル・ハンティング』のような本格的な数学映画でさえ、数学を完全に台無しにしてしまうことがよくある。

ヤング・シェルドン シーズン3エピソード4「ホビット、物理学者、そしてジッパー付きボール」で、シェルドンはビンゴカードの組み合わせが何通りあるか自問します。答えは何でしょうか？また、番組で示された計算式は正しいでしょうか？

匿名

まず、順列の数について見ていきましょう。これは、数字だけでなく、カード上の順番も重要だということです。B、I、G、O列には、permut(15,5) = 15!/(15-5)! = 15*14*13*12*11 = 360,360通りの順列があります。N列の場合、順列の数はpermut(14,4) = 15!/(15-4)! = 15*14*13*12 = 32,760通りです。したがって、ビンゴカードの順列の総数は、360,360 4 × 32,760 = 552446474061128648601600000通りです。

次に、組み合わせの数について見ていきましょう。つまり、数字自体は重要ですが、カード上の順番は重要ではありません。B、I、G、O列の組み合わせは、combin(15,5) = 15!/(5!*(15-5)!) = (15*14*13*12*11)/(1*2*3*4*5) = 3,003通りあります。N列の組み合わせは、combin(14,4) = 15!/(4!*(15-4)!) = (15*14*13*12)/(1*2*3*4) = 1,365通りです。したがって、ビンゴカードの組み合わせの総数は、3,003 4 × 1,365 = 111007923832370565通りです。

ys1

イース2

番組の中で、シェルドンは「ユニークなビンゴカードはいくつ存在するのか」と自問します。後半の間違った計算式から判断すると、彼は順列を意味していると思われます。つまり、同じ数字で位置が異なる2枚のカードは、どちらも「ユニーク」であるということです。

ヤングシェルドンビンゴ3

上の画像は、シェルドンがB、I、G、O列について示した式です。彼は最初、5! × combin(15,5) で正しい式を導き出しました。しかし、誤って15!/(15!-5)! と簡略化しています。2つ目の感嘆符は本来あるべきではありません。正しくは15!/(15-10)! です。しかし、その後、360,360 で正しい答えに戻ります。

ヤングシェルドンビンゴ4

N列でも全く同じ問題があります。式は15!/(15-4)!ではなく、15!/(15!-4)!とすべきです。2つ目の感嘆符が台無しにしています。

皮肉なことに、エピソード後半で、シェルドンは、私がこれに夢中になっているのと同じように、「ロード オブ ザ リング」の年代順の誤りに夢中になります。

ヤングシェルドンビンゴ4

100リットルのタンクに水と10kgの塩が入っています。1分間に10リットルの純水を加え、同時に1分間に10リットルの溶液を排出すると、30分後にタンクに残っている塩の量はどれくらいでしょうか？

Ace2

まず、いくつかの変数を定義しましょう。

  • s = タンク内の塩のkg
  • t = 塩がタンクに投入されてからの経過時間（分）

1分間に塩の10%が排出されると仮定します。これを数学的に表すと次のようになります。

ds/dt = (-10/100) × s

これを次のように並べ替えてみましょう。

ds = (-10/100) × s dt

-10/s ds = dt

双方を統合する:

(1) -10×ln(s) = t + c

次に、厄介な積分定数を求めましょう。そのためには、t = 0のときs = 10であることが与えられています。これを上の式(1)に代入すると、次のようになります。

-10 × ln(10) = 0 + c

つまりc = -10×ln(10)

これを式（1）に代入すると次のようになります。

(2) -10×ln(s) = t -10×ln(10)

ここで問題となるのは、t=30の時点でタンク内の塩の量がどれくらいになるかということです。t=30の時点でのsについて解くと、次のようになります。

-10×ln(s) = 30 -10×ln(10)。次に両辺を-10で割ります…

ln(s) = -3 + ln(10)

s = exp(-3 + ln(10))

s = exp(-3) × exp(ln(10))

s = exp(-3) × 10

s =~ 0.4979 kgの塩。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

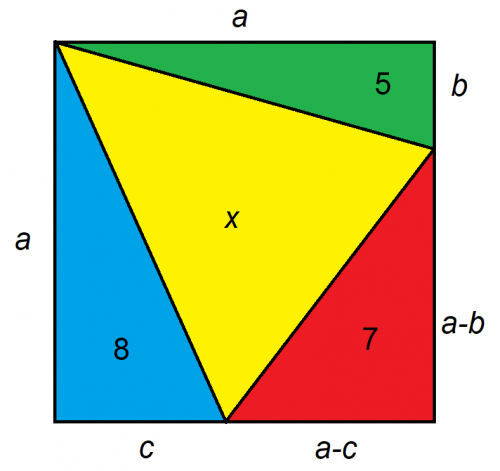
大きい方の図形が正方形である場合、x の面積はいくらでしょうか?

Dyana から Las Vegas

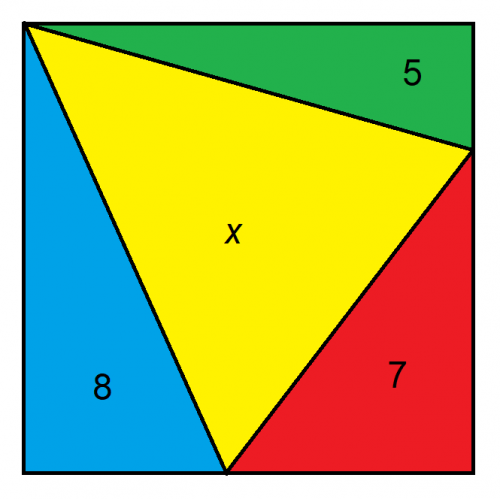
このような問題を解く鍵は、その設定にあります。問題をできるだけ少ない未知数に絞り込むことをお勧めします。この場合、正方形上の未知数の距離は、次のように3つに絞られます。

正方形の解の中に4つの三角形

三角形よりも長方形の方が扱いやすいです。3つの三角形の面積が分かっていれば、大きさと面積を2倍にすることができます。つまり、次のようになります。

  • ab=10
  • ac=16
  • (ab)(ac)=14

(ab)(ac)を因数分解してみましょう。

a 2 - ab- ac + bc = 14

2 - 10 - 16 + bc = 14

（1）a 2 + bc = 40

これを 1 つの変数にするために、b と c を a で表してみましょう。

b = 10/a

c = 16/a

これらの値を式(1)のbとcに代入すると、

a 2 + (10/a)*(16/a) = 40

a 2 + 160/a 2 = 18

次に、すべてに2を掛けて、分母の2 を取り除きます。

4 + 160 = 40 * 2

4 - 40 * 2 + 160 = 0

新しい変数y = a 2を定義しましょう

y 2 - 18y + 32 = 0

次に、二次方程式を使って y を解きます。

y = (40 +/- 平方根(1600-640))/2

y = (40 +/- 平方根(960))/2

y = (40 +/- 8*sqrt(15))/2

y = 20 +/- 4*sqrt(15)

正方形全体の面積はa 2で、これは都合よくyと等しくなります。上の式から、+/-が負の場合、y = apx 4.5081となりますが、これは明らかに誤りです。なぜなら、面積はxを含めなくても少なくとも20であるからです。したがって、正方形の面積は20 + 4*sqrt(15) となるはずです。

与えられた3つの三角形の面積は5+7+8=20です。これを正方形の総面積から引くと、xの面積は20 + 4*sqrt(15) - 20 = 4*sqrt(15) = 約15.4919になります。

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。

サンコースト

この写真の私のTシャツに注目してください。映画『 アンカット・ジェムズ』を見に行った時、映画館のレジ係の人がそれを褒めてくれました。お礼に、面積2、3、4の三角形だけを使ったこの問題で彼女を苦しめました。映画が終わって彼女に確認すると、まだ解けていなかったものの、頑張っているようでした。そこで、サンコーストのバーで次の解法を彼女に書いてあげました。彼女は本当に喜んでくれたようでした。この若い女性はきっと将来大成するでしょう。

1次元×1次元の正方形のダーツボードがあります。ダーツを投げると、どの場所にも等確率で着地します。ダーツが着地する座標を(x,y)とします。ここで、xとyは0から1まで均一かつ独立に分布します。

z = round(x/y) とします。言い換えると、z = x/y を最も近い整数に丸めます。z が偶数である確率はどれくらいでしょうか？

匿名

次のヒントの無限級数を知っておくと非常に役立ちます。

[ネタバレ=ヒント]

ライプニッツのπの公式は次の通りです。

1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4

[/spoiler]

回答のみを知りたい場合は、次のボタンをクリックしてください。

[ネタバレ=答え](5 - π)/4 = 約。 0.464601836602552。 [/spoiler]

解決策については下のボタンをクリックしてください。

x/y < 0.5 の場合、比は n を 0 に切り捨て、偶数になります。ダーツボード上の (0,0) と (0.5) で形成される直線の左側にある点は、いずれも 0 に切り捨てられます。その面積は、1 と 1/2 の辺を持つ直角三角形です。三角形の面積は (1/2)*底辺*高さであることを覚えておいてください。したがって、0 を切り捨てたこれらの点の面積は (1/2)*(1/2) = 1/4 です。

グラフ上で次に偶数である2に丸められる領域は、1.5 < x/y < 2.5のときです。この領域は、底辺が2/3 - 2/5、高さが1の三角形になります。これらはx/yの境界の逆数であることに注意しましょう。xは1なので、yを反転する必要があります。つまり、2に丸められる領域は(1/2)*(2/3 - 2/5)です。

グラフ上で次に偶数である4に丸められる領域は、3.5 < x/y < 4.5のときです。この領域は、底辺が2/7 - 2/9、高さが1の三角形になります。したがって、2に丸められる領域は(1/2)*(2/7 - 2/9)です。

グラフ上で次に偶数である6に丸められる領域は、5.5 < x/y < 6.5のときです。この領域は、底辺が2/11 - 2/13、高さが1の三角形になります。したがって、2に丸められる領域は(1/2)*(2/11 - 2/13)です。

パターンが見えてきましたか？それは次のようになります。

1/4 + 1/2*(2/3 - 2/5 + 2/7 - 2/9 + 2/11 - 2/13 + ...) =

1/4 + (1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =

括弧内に -1 を移動しましょう。

5/4 + (-1 + 1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =

5/4 - (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 + ... ) =

次に、上記のヒントを思い出してください。

1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11

さて、本題に戻りますが...

5/4 - π/4 =

(5 - π) / 4 = 約。 0.464601836602552。

π と e が数学のあちこちで頻繁に登場するのは興味深いですね。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

9 x + 12 x = 16 xとします

xとは何ですか?

匿名

答えについては下のボタンをクリックしてください。

x = [ln(1 + sqrt(5)) - ln(2)] / [ln(4) - ln(3) ] = 約 1.67272093446233.

解決策については下のボタンをクリックしてください。

9 x + 12 x = 16 x =

両辺を9で割る

1 + (12/9) x = (16/9) x

1 + (4/3) x = ((4/3) x ) 2

（１）u = (4/3) xとします

1 + u = u 2

二次方程式により...

u = (1+sqrt(5)) / 2 (黄金比)

これを式(1)に戻すと次のようになります。

(4/3) x = (1+sqrt(5)) / 2

両辺の対数をとります。

x ln(4/3) = ln[(1+sqrt(5)) / 2]

x = ln[(1+sqrt(5)) / 2] / ln(4/3)

x = [ln(1+sqrt(5) - ln(2)] / [ln(4) - ln(3)] = 約 1.67272093446233.

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。

謝辞: この問題のバリエーションは、Mind Your Decisionsの Presh Talwalkar 氏から提供されました。

ある農家がリンゴの種を5つ植えました。1日ごとに、それぞれの種が発芽する確率は1/3です。5本の木すべてが発芽するまでの平均時間はどれくらいでしょうか？

匿名

答えは約6.131415853日です。

農家がリンゴの種を5つ植えました。1日ごとに、それぞれの種が発芽する確率は1/3です。5本の木すべてが発芽するまでの平均時間はどれくらいでしょうか？

逆算してみましょう。発芽していない種子が1つ残っている場合、発芽するまでに平均1/p日かかります。ここでpは、ある特定の日に発芽する確率です。p = 1/3なので、発芽するまでに平均3日かかります。これをt 1 = 3としましょう。

種が2つ残っていたらどうでしょう？翌日に両方とも発芽する確率はap 2 = 1/9で、これで終わりです。翌日に片方の種が発芽する確率は2×p×qで、qは発芽しない確率です。したがって、片方の種が発芽する確率は2×(1/3)(2/3) = 4/9です。どちらの種も発芽しない確率はq 2 = (2/3) 2 = 4/9です。2つの種が発芽する期待日数をt 2としましょう。

t 2 = 1 + (4/9)×t 1 + (4/9)t 2

t 2 = (1 - (4/9)) = 1 + (4/9)×t 1

t 2 = (1 + (4/9)×3) / (1 - (4/9))

t 2 = (21/9) / (5/9)

t 2 = (21/9) × (9/5) = 21/5 = 4.2

残りの種が3つだったらどうでしょう？翌日にすべてが発芽して終わりになる確率は ap 3 = 1/27 です。翌日に1つ発芽する確率は 3×p×q 2 = 3×(1/3)(2/3) 2 = 12/27 です。翌日に2つ発芽する確率は 3×p 2 ×q = 3×(1/3) 2 ×(2/3) = 6/27 です。発芽しない確率は q 3 = (2/3) 3 = 8/27 です。3つの種が発芽する期待日数を t 3としましょう。

t 3 = 1 + (6/27)t 1 + (12/27)×t 2 + (8/27)×t 3

t 3 = 1 + (6/27)×3 + (12/27)×4.2 + (8/27)×t 3

t 3 × (1 - 8/27) = (1 + 18/27 + 28/15)

t 3 = (1 + 18/27 + 28/15) / (1 - 8/27) = 477/95 = 約 5.02105263

残りの種が4つあったらどうでしょう？翌日に4つすべてが発芽して終わりになる確率はap 4 = 1/81です。翌日に1つが発芽する確率は、4×p×q 3 = 4×(1/3)(2/3) 3 = 32/81です。翌日に2つが発芽する確率は、combin(4,2)×p 2 ×q 2 = 6×(1/3) 2 ×(2/3) 2 = 24/81です。翌日に3つが発芽する確率は、combin(4,3)×p 3 ×q = 4×(1/3) 3 ×(2/3) = 8/81です。発芽しない種が1つもない確率は、q 4 = (2/3) 4 = 16/81です。3つの種が発芽する期待日数をt 4としましょう。

t 4 = 1 + (8/81)×t 1 + (24/81)×t 2 + (32/81)×t 3 + (16/81)×t 4

t 4 = 1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263 + (16/81)×t 4

t 4 = (1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263) / (1 - (16/81))

t 4 = 約 5.638056680161943319838056680。

5粒全部残っていたらどうでしょう？5粒すべてが翌日に発芽して終わりになる確率はap 5 = 1/243です。翌日に1粒が発芽する確率は、5×p×q 4 = 5×(1/3)(2/3) 4 = 80/243です。翌日に2粒が発芽する確率は、combin(5,2)×p 2 ×q 3 = 10×(1/3) 2 ×(2/3) 3 = 80/243です。翌日に3粒が発芽する確率は、combin(5,3)×p 3 ×q = 10×(1/3) 3 ×(2/3) 2 = 40/243です。翌日に4粒が発芽する確率は、combin(5,4)×p 4 ×q = 5×(1/3) 4 ×(2/3) = 10/243です。発芽しない確率は、q 5 = (2/3) 5 = 32/243です。3粒の発芽が期待される日数をt 5としましょう。

t 5 = 1 + (10/243)×t 1 + (40/243)×t 2 + (80/81)×t 3 + (80/243)×t 4 + (32/243)×t 5

t 5 = (1 + (10/243)×t 1 + (40/243)×t 2 + (80/81)×t 3 + (80/243)×t 4 ) / (1 - (32/243))

t 5 = (1 + (10/243)×3 + (40/243)×4.2 + (80/243)×(477/95) + (80/243)×5.63805668) / (1 - (32/243))

t 5 = 約 6.131415853。

この問題は、Mind Your Decisionsの Presh Talwalkar による同様の問題を基に作成されました。

質問は2つあります。

パート 1 の場合:
  • x + y + z = 1
  • x^2 + y^2 + z^2 = 4
  • x^3 + y^3 + z^3 = 9

x^4 + y^4 + z^4 とは何ですか?

2 番目の部分では、次のような一般的なケースの答えは何ですか。

  • x + y + z = a
  • x^2 + y^2 + z^2 = b
  • x^3 + y^3 + z^3 = c

匿名

問1: 97/6 = 約16.166666

問2: a 4 /6 + (4/3)ac - a 2 b + b 2 /2

私の解決策（PDF）をご覧ください

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。

微生物、例えばCOVID-20は、いつでも新しい微生物を生み出す可能性があります。特定の親微生物から特定の微生物が特定の時点で生まれる確率は、前回の産卵からの経過時間に関わらず、常に一定です。同じ微生物から産卵する平均間隔は1日です。数学的に言えば、同じ微生物から産卵する期待間隔は、平均1日の指数分布に従います。

微生物が肺に入ると、7日後にはどれくらいの微生物が存在すると予想されますか?

匿名

答えについては下のボタンをクリックしてください。

答えは e 7 = 約 1,096.6332 です。

解決策については下のボタンをクリックしてください。

この解法には常微分方程式が必要です。数学教育でまだその段階に達していないなら、理解できないでしょう。

させて：
m = COVID-20の微生物の数
t = 時間（日数）

各微生物は平均して1日に1回、新たな微生物を産生するため、m個の微生物は平均して1日にm個の新たな微生物を産生することになります。言い換えれば、任意の時刻tにおける微生物の増加率（m）は次のように表すことができます。

dm/dt = m です。

これをどう表現するのが適切か分かりませんが、dt を右側に分離します。

dm = m dt。

両辺をmで割ります。

1/m dm = 1 dt。

両辺を統合します。

ln(m) = t + C、ここでCは積分定数です。

時刻0には微生物が1個存在すると仮定します。つまり、t = 0のとき、m = 1です。これらの値を上記の式に代入してCを解きます。

ln(1) = 0 + C

0 = 0 + C

C = 0です。

これでln(m) = tとなります。

両辺のexp()を取ります。

m = e t

したがって、時刻 t=7 では、e 7 = 約 1096.6332 個の微生物が存在することになります。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

古い西部の酒場で、トランプゲームをめぐる口論がエスカレートし、付近のカウボーイ全員が銃を抜いて互いに撃ち合う事態となった。

煙がようやく晴れると、カウボーイの90%が脚を、85%が腕を、80%が腹部を、そして75%が頭部を撃たれていた。驚くべきことに、この激しい銃撃戦で命を落としたのは、これら4種類の傷をすべて負ったカウボーイだけだった。

最終的に埋葬されたカウボーイの最小の割合はどれくらいでしょうか?

Gialmere

30%

まず、カウボーイの90%の脚を撃ちます。

次に、腕に残っている10%を撃ちます。腕に撃つべき敵はあと75%いるので、脚を撃たれた敵から腕を奪い取ります。

つまり、今は次のようになります。

脚のみ 15% (90% - 75%)
腕のみ10％
両方とも75%
どちらも0%

合計脚：90％
腕全体: 85%

次に、腹部の損傷（80%）について見ていきましょう。腹部の損傷が片方だけの25%を撮影します。80%-25% = 55%の人が撮影対象となります。この55%は、両方の損傷がある人の中から選びます。つまり、以下のようになります。

脚と内臓 15%
腕と腸 10%
脚と腕 20% (75% - 55%)
3つすべて55%
負傷者1人 0%
負傷者ゼロ 0%

最後に、頭部損傷のある75%について考えてみましょう。まず、ちょうど2つの損傷がある45%を狙います。あと30%残っているので、3つの損傷すべてがある55%から狙います。つまり、以下のようになります。

頭、脚、内臓 15%
頭、腕、内臓 10%
頭、脚、腕 20%
脚、腕、腸: 25% (55% - 30%)
4つすべて30%
負傷者ゼロ 0%
負傷者1人 0%
負傷者2名 0%

[ネタバレ=CharliePatrickの解決策]

カウボーイが20人いるとしましょう。この数字を選んだのは、関係する確率はすべて5%で割り切れ、20の5%は1だからです。

一列に並べます。左から順に、90%、つまり18発を脚に撃ちます。次に、上段にカウボーイナンバー、左列にそれぞれの負傷者数を記した図を作成します。

けが1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L L
2
3
4
合計1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0

次に、腕を85%、つまり17発撃つ必要があります。まず、脚を撃たれていない2人のカウボーイから始めましょう。あと15発です。左のカウボーイに戻り、列を下がって、脚を撃たれた合計15発を撃ちます。負傷カードは次のようになります。

けが1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L Lああ
2あああああああああああああああ
3
4
合計2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1

次に、80%、つまり16発の腹を撃つ必要があります。まず、負傷が1発だけのカウボーイ5人から始めましょう。残りは11発です。左のカウボーイに戻り、列を下がっていき、既に2発撃っている合計11発を撃ちます。負傷カードは以下のようになります。

けが1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L Lああ
2あああああああああああああああG G G G G
3 G G G G G G G G G G G
4
合計3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2

次に、75%、つまり頭部に15発撃つ必要があります。まず、2発しか撃たれていない9人のカウボーイから始めましょう。あと6人です。左のカウボーイに戻り、列を下に移動して、すでに3発撃たれている6人を撃ちます。負傷カードは次のようになります。

けが1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L Lああ
2あああああああああああああああG G G G G
3 G G G G G G G G G G G H H H H H H H H H
4 H H H H H H
合計4 4 4 4 4 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3

ご覧の通り、6人のカウボーイが4回、14人が3回撃たれています。したがって、3回のみの負傷で済む最大確率は14/20 = 70%です。

一般的なケースでは、4 つの確率が a、b、c、d の場合、a+b+c+d >=3 かつ a+b+c+d <=4 である限り、生き残ることができる最大比率は 1-(a+b+c+d) になります。

この解決策を提供してくれた Wizard of Vegas フォーラム メンバーの CharliePatrick に感謝の意を表したいと思います。

[/spoiler]

この質問は、 この投稿から始まり、私のフォーラムで尋ねられ、議論されています。

カエルは1フィートまたは2フィートジャンプできます。カエルは常に前方へジャンプし、合計でちょうど10フィートを複数回ジャンプします。ジャンプの距離と順序を考慮すると、このジャンプは何通りの方法で行うことができますか？

匿名

89

  1. カエルが片足だけでジャンプする必要がある場合、明らかに方法は一つしかありません。カエルは目標を飛び越えることはできないことを覚えておいてください。
  2. カエルが 2 フィートジャンプする必要がある場合、これには 2 つの方法があります -- (1) 1 フィートと 1 フィート、または (2) 2 フィートです。

    3. カエルが3フィートジャンプする必要がある場合、最後のジャンプの前に1フィートまたは2フィート離れている可能性があります。ステップ1で示したように、2フィート離れる方法は1つあり、ステップ2で示したように、1フィート離れる方法は2つあります。したがって、3フィートジャンプする方法は3つあります。これは、(1) 1+1+1、(2) 1+2、(3) 2+1 と簡単に証明できます。

    カエルが4フィートジャンプする必要がある場合、最後のジャンプの前に2フィートまたは3フィート離れている可能性があります。ステップ2に示すように、2フィート離れる方法は2通りあり、ステップ3に示すように、1フィート離れる方法は3通りあります。したがって、4フィート離れる方法は5通りあります。これは、(1) 1+1+1+1、(2) 1+1+2、(3) 1+2+1、(4) 2+1+1、(5) 2+2 と簡単に証明できます。

    カエルが5フィートジャンプする必要がある場合、最後のジャンプの前に3フィートまたは4フィート離れている可能性があります。ステップ3に示すように、2フィート離れる方法は3通りあり、ステップ4に示すように、1フィート離れる方法は5通りあります。したがって、5フィート離れる方法は3+5=8通りあります。これは、(1) 1+1+1+1+1、(2) 1+1+1+2、(3) 1+1+2+1、(4) 1+2+1+1、(5) 2+1+1+1、(6) 2+2+1、(7) 2+1+2、(8) 1+2+2 と簡単に証明できます。

    パターンが見えてきましたか？それはフィボナッチ数列です。同じ論理を続けると、カエルがちょうど合計10フィートジャンプする方法は89通りあります。

米国の標準的な硬貨である 1、5、10、25、50 セント、1 ドルを使って、1 ドルのお釣りを出す方法はいくつありますか?

Gialmere

答えは293です。

a(x) を、ペニーとニッケルのみを使用して x セントを作る方法の数とします。ここで、x は 5 で割り切れます。

a(x) = 1+(x/5)

言い換えれば、方法の数は、お釣りの可能なニッケルの数であり、範囲は 0 から x/5 になります。

b(x) を、ペニー、ニッケル、ダイムのみを使用して x セントを作る方法の数とします。ここで、x は 5 で割り切れます。

b(0)=1
b(5)=2
b(x) = a(x) + b(x-10)、ただしx>=10。

簡単に言えば、x セントを稼ぐ方法の数は、(1) b(x-10) = 各方法に 10 セントずつ加えて x-10 セントにする方法の数と、(2) a(x) = 10 セントを使わない方法の数の合計です。

c(x) を、ペニー、ニッケル、ダイム、クォーターのみを使用して x セントを作る方法の数とします。ここで、x は 25 で割り切れます。

c(0) = 1
c(x) = b(x) + c(x-25)、ただしx>=25。

簡単に言えば、x セントを儲ける方法の数は、(1) c(x-25) = 各方法に 25 セントずつ加えて x-25 セントにする方法の数と、(2) b(x) = 25 セントを使わない方法の数の合計です。

d(x) を、ペニー、ニッケル、ダイム、クォーター、ハーフドルのみを使用して x セントを作る方法の数とします。ここで、x は 50 で割り切れます。

d(0) = 1
d(x) = c(x) + d(x-50)、ただしx>=50。

簡単に言えば、x セントを稼ぐ方法の数は、(1) d(x-50) = 各方法に 0.5 ドルを追加して x-50 セントを得る方法の数と、(2) c(x) = 0.5 ドルを使わない方法の数の合計です。

以下は、x = 5 ～ 100 の場合のこれらの値を示す表です。

変化を起こす方法

×斧） b(x) c(x) d(x)
0 1 1 1
5 2 2 0
10 3 4 0
15 4 6 0
20 5 9 0
25 6 12 13
30 7 16 0
35 8 20 0
40 9 25 0
45 10 30 0
50 11 36 49 50
55 12 42 0
60 13 49 0
65 14 56 0
70 15 64 0
75 16 72 121
80 17 81 0
85 18 90 0
90 19 100 0
95 20 110 0
100 21 121 242 292

最後に、1 ドル硬貨に 1 を加えると、答えは 292+1 = 293 になります。

この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。

電球は無数にあり、すべて消灯しています。電球が点灯する間隔は、平均1日の指数分布*に従います。電球が一度点灯すると、その寿命も平均1日の指数分布に従います。

最初の電球が切れるまでの平均時間はどれくらいですか?

*: 指数分布に従うランダム事象は、過去が関係ないという点で記憶のない性質を持ちます。言い換えれば、単一の事象が期限切れになることはなく、発生する確率は常に一定です。

Ace2

答えは e - 1 = 約 1.7182818... です。

最初の電球が点灯するまでに平均1日かかります。

そこから、次の重要なイベント（新しい電球が点灯するか、最初の電球が切れるか）まで、平均して半日かかります。そのイベントまでの待ち時間に半日を加えます。つまり、1 + (1/2) = 1.5日となります。

2番目のイベントが2つ目の電球の点灯である確率は1/2です。その場合、次の重要なイベント（最初の2つの電球のどちらかが切れるか、新しい電球が点灯するか）まで1/3日の待機時間があります。したがって、1/2（ここまでの確率）と1/3を掛け合わせた1/6を待機時間に加えます。つまり、1.5 + 1/6 = 5/3 = 1.66667日ではありません。

3番目の重要なイベントが3つ目の電球の点灯である確率は(1/2)*(1/3) = 1/6です。この場合、次の重要なイベント（最初の3つの電球のいずれかが切れるか、新しい電球が点灯するかのいずれか）まで1/4日の待機時間があります。したがって、1/6（ここまでの確率）と1/4を掛け合わせた値である1/24を待機時間に加えます。つまり、5/3 + 1/24 = 41/24 = 1.7083日ではありません。

このパターンに従うと、答えは (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ... となります。

e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ... であることは周知の事実です。

唯一の違いは、答えに1/0! 係数がないことです。したがって、答えは e - 1/0! = e - 1 = 約 1.7182818... となります。

この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

A、B、C、D はすべて異なる正の整数です。

A < B < C < D

最大のDを求めて

1/A + 1/B + 1/C + 1/D = 1

Gialmere

答えは42です。A、B、Cはそれぞれ2、3、7です。

1/2 + 1/3 + 1/7 + 1/42 = 1。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

クイーンズ・ギャンビットを最後まで観て、番組で流れていたゲームがどれも引き分けで終わっていないことに気づきました。チェスではハイレベルな試合は引き分けが多いと思っていたのですが、グランドマスターレベルのチェスでは、引き分けで終わる割合はどれくらいですか？

匿名

ChessBase.com の記事「チェスの引き分けの数は増加したか?」によると、著者の Qiyu Zhou 氏は、レート 2600 以上 (グランドマスターになるには 2500 が必要) のプレイヤー間の 78,468 回のレート付きゲームで、次のような結果になったと述べています。

  • 黒の勝ち: 18.0%
  • 白の勝ち: 28.9%
  • 引き分け: 53.1%

5×5のペグボードと3本のペグがあります。ランダムに配置された3本のペグが三角形を形成する確率はどれくらいでしょうか？

匿名

93.39%

まず、ペグの組み合わせは combin(25,3) = 2,300 通りあります。

これらの組み合わせのうち、いくつが三角形を形成しますか？このボードを使って考えてみましょう。

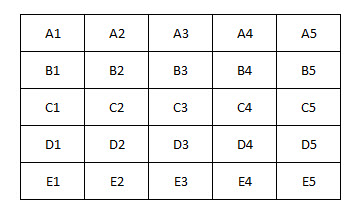
ペグボード

まず、5つの行、5つの列、そして2つの対角線があります。これらのいずれの場合も、ペグを一列に並べる方法はcombin(5,3) = 10通りあります。つまり、12*10 = 120通りの組み合わせがあります。

次に、行/列の中央のマス目を隣接する行/列の中央のマス目に接続する方法は4つあります。つまり、以下の3つの配置です。

  • A3、B4、C5
  • C5、D4、E3
  • E3、D2、C1
  • C1、B2、A3

つまり、120 + 4 = 124です

3 番目に、4 つのスペースである 4 つの異なる対角線があります。

  • A2、B3、C4、D5
  • B5、C4、D3、E2
  • E4、D3、C2、B1
  • D1、C2、B3、A4

それぞれについて、3本のペグを配置する方法はcombin(4,3)=4通りあります。つまり、4×4=16通りになります。

今は124+16=140です

4つ目に、チェスのナイトの動き方を考えてみましょう。2x1のL字型です。各コーナーには、ナイトが動ける2通りの方法があります。どちらの場合も、ナイトは最初の動きと同じ線に沿って再び動くことができます。つまり、4x2 = 8通りの動きができます。

  • A1、C2、E3 A1、B3、C5
  • A5、B3、C1
  • A5、C4、E3
  • E5、C4、A3
  • E5、D3、C1
  • E1、D3、C5
  • E1、C2、A3

中央を通るナイト ラインも 4 つあります。

  • A2、C3、E4
  • A4、C3、E2
  • B5、C3、D1
  • D5、C3、B1

12のナイトラインを加えると、140+12=152になります。

合計 2,300 通りの組み合わせがあり、そのうち 152 通りが直線になる場合、2300 - 152 = 2,148 通りは直線にならず、三角形になります。

したがって、答えは 2,148/2,300 = 93.39% となります。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

あなたに与えられるもの:

  • その時、地対空ミサイルが発射され、そのミサイルの真上８マイルに飛行機がいた。
  • 飛行機は常に一直線に進みます。
  • 飛行機は時速600マイルで飛行します。
  • ミサイルは時速2000マイルで飛行します。
  • ミサイルは常に飛行機に正面から向く角度で飛行します。

質問:

  • ミサイルに撃たれるまでに飛行機はどれくらいの距離を飛行するのでしょうか？
  • ミサイルが飛行機に命中するまでにどれくらい時間がかかりますか？
  • ミサイルの飛行経路はどれくらいですか？

匿名

  • ミサイルが命中するまでに飛行機はどれくらいの距離を飛行するでしょうか？ = 240/91マイル
  • ミサイルが飛行機に命中するまでにどれくらいの時間がかかりますか？ = 2/455時間
  • ミサイルはどれくらい飛行しますか？ = 800/91マイル

これが私の解決策です（PDF）。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

仮定する：

  • 国民の90％がマスクを着用しています。
  • コロナウイルスに感染する確率は、マスク着用者で1％、非着用者で3％です。

コロナウイルスに感染した人がランダムに選ばれます。その人がマスクを着用している確率はどれくらいでしょうか？

匿名

これは典型的なベイズ条件付き確率の問題です。

答えは、確率（誰かがマスクを着用していてコロナウイルスに感染している）/確率（誰かがコロナウイルスに感染している）=

(0.9*0.01) / (0.9*0.01 + 0.1*0.03) = 75% です。

正方形の真ん中にアリがいます。アリは左上隅から17インチ、右上隅から20インチ、右下隅から13インチのところにいます。

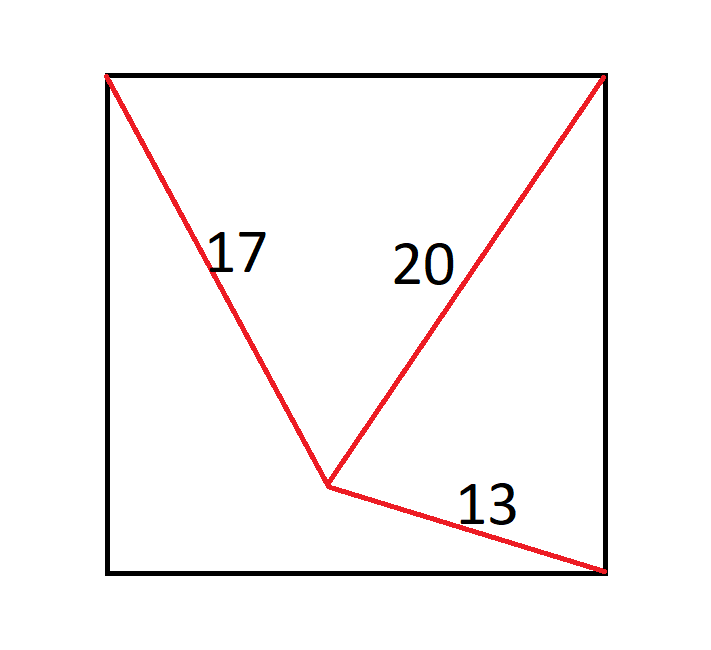
広場の大きさはどれくらいですか？

匿名

c^2 = a^2 + b^2 -2ab*cos(c)
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)

369平方インチ。

まず、三角形 ABE を 90 度回転して、新しい三角形 BDF を形成します。

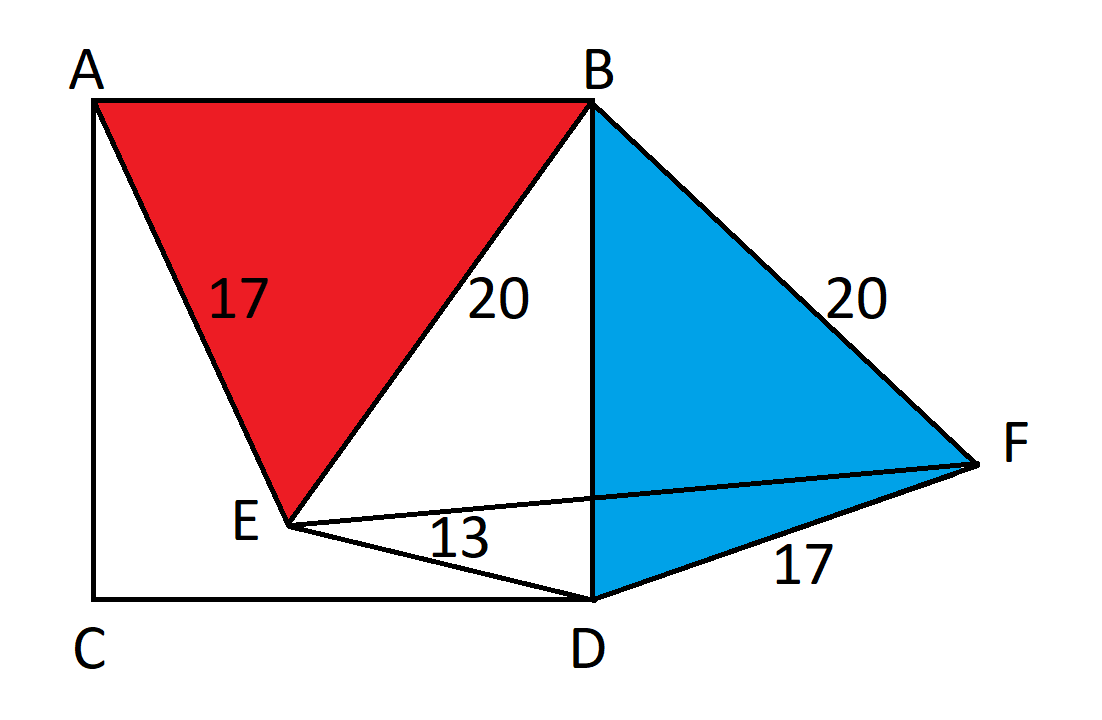
三角形は90度回転しているので、定義により、角EBF=90となります。ピタゴラスの定理によれば、EF = 20*sqrt(2)となります。

余弦定理によれば、17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF)となります。

289 = 169 + 800 - 520*sqrt(2)*cos(DEF)

520*sqrt(2)*cos(DEF) = 680。

cos(DEF) = 17*sqrt(2)/26。

sin^2(x) + cos^2(x) = 1 を思い出してください。これを使って sin(DEF) を解きましょう。

sin^2(DEF) + cos^2(DEF) = 1

sin^2(DEF) + (17*sqrt(2)/26)^2 = 1

sin^2(DEF) + 289/338 = 1

sin^2(DEF) = 49/338

sin(DEF) = 7*sqrt(2)/26

次に、角度 BED について考えます。

角度 BED = 角度 BEF + 角度 FED。

EBFは90度で二等辺三角形であることが分かっています。つまり、BEFの角度は45度になります。

つまり、角度 BED = 45 度 + 角度 FED となります。

思い出してください、cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)。

cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)

= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26

= (17/26) - (7/26) = 10/26 = 5/13

今度は三角形 BED に余弦定理をもう一度適用してみましょう。

BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)

= 400 + 169 - 200 = 369

BD は問題の正方形の辺なので、BD^2 はその正方形の面積であり、369 であることが示されています。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

あなたは遊園地の夜間花火大会を担当する花火師です。ヨーロッパから新型ロケットを入手し、ショーのBGMに合わせて打ち上げるタイミングをテストしています。

花火ロケットは、化学燃料が尽きるまで4ms^-2の一定加速度で垂直上方に発射されます。その後、重力によって上昇速度が減速され、最高高度138メートルに到達して爆発します。

空気抵抗がなく、重力加速度が毎秒 9.8 メートルであると仮定すると、ロケットが最高高度に到達するまでにどれくらいの時間がかかりますか?

Gialmere

答えは483/49 = 約9.8571秒です。

させて：
t = ロケット燃料がなくなるまでの時間。
r = ロケット燃料が持続した時間。

加速度を上向きの方向で表します。つまり、ロケット燃料が燃え尽きた後の加速度は-9.8です。

念のため、加速度の積分は速度であり、速度の積分は位置です。位置を地面を基準にしてみましょう。

ロケットが最初に打ち上げられるとき、加速度は 4 であると与えられます。

積分すると、r 秒後のロケットの速度は 4r になります。

速度を積分すると、2r 2の r 秒後のロケットの位置が得られます。

それでは、ロケット燃料が燃え尽きた後に何が起こるかを見てみましょう。

重力加速度は -9.8 であると与えられています。

時刻tにおける重力速度は-9.8tです。しかし、ロケットから4rの上向きの速度も持っています。

v(t) = 時刻tにおける速度とする

v(t) = -9.8t + 4r

ロケットはv(t) = 0のときに最大高度に達します。これを解いてみましょう。

v(t) = 0 = -9.8t + 4r
4r = 9.8t
t = 40/98 r = 20r/49。

言い換えれば、ロケット燃料がどれだけの時間持続したとしても、ロケットはその時間のうち 20/49 の間上昇し続けることになります。

また、達成された最高高度での移動距離は 138 であることが示されています。

v(t) を積分して移動距離の式を取得し、これを d(t) と呼びます。

d(t) = -4.9t 2 + 4rt + c、ここでcは積分定数です。

すでに示したように、燃料が燃え尽きるまでにロケットは2r 2を移動したので、これが積分定数となるはずです。つまり、

d(t) = -4.9t 2 + 4rt + 2r 2

最高高度 138 に到達したのは 20r/49 の時刻であることが分かっています。そこで、t=20r/49 を式に代入して r について解きます。

d((20r/49) = -4.9((20r/49) 2 + 4r(20r/49) + 2r 2 = 138

r 2 * (-1960/2401 + 80/49 + 2) = 138

r 2 = 49

r = 7

つまり、ロケット燃料は 7 秒間持続しました。

ロケットがその時間のうち 20/49 秒間上昇し続けたことはすでにわかっています。つまり、140/49 = 約 2.8571 秒です。

したがって、打ち上げから最大速度までの時間は7 + 140/49 = 483/49 = 約9.8571秒となる。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

2つのサイコロを振って、2から12までの合計が出るまでの予想回数はいくつですか？ 微積分を使って答えてください。

BruceZ

約61.2173847639572ロールです。

合計が2になる確率は1/36であることを思い出してください。t回振った場合、合計が2になる期待値はt/36です。振る間隔は平均t/36の指数分布に従うと仮定します。ポアソン分布によれば、合計が2になる0回の確率はexp(-t/36)です。

合計が3になる確率は2/36 = 1/18であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が3でサイコロが0回出る確率はexp(-t/18)となります。

合計が4になる確率は3/36 = 1/12であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が4でサイコロが0回出る確率はexp(-t/12)となります。

合計が5になる確率は4/36 = 1/9であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が5でサイコロが0回出る確率はexp(-t/9)となります。

合計が6になる確率は5/36であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が6でサイコロが0回出る確率はexp(-5t/36)となります。

合計が7になる確率は6/36 = 1/6であることを思い出してください。同じ論理で、ポアソン分布によれば、合計が7でサイコロが0回出る確率はexp(-t/6)となります。

8 から 12 までの確率は 2 から 6 までの確率と同じです。

したがって、t 単位のあらゆる合計が少なくとも 1 回ロールされる確率は次のとおりです。

(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))

t単位の時間内に少なくとも合計が出ていない確率は、1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))です。

少なくとも 1 つの合計なしで予想時間を取得するには、上記の関数を 0 から無限大まで積分します。

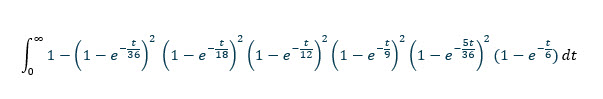
積分計算機 (これをお勧めします) を使用すると、769767316159/12574325400 = 約 61.2173847639572 ロールとして簡単に解くことができます。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

直方体は、単位正方形で構成された 3 次元のブロックです。

直方体

a × b × c の直方体は、3x3x3 のルービックキューブのように、abc 個の同一の単位立方体で構成されています。立方体を互いに排他的な2つのタイプに分けます。外側の立方体とは、直方体の面を構成する立方体で、内側の立方体は完全に閉じた立方体です。例えば、図の直方体には、外側の立方体が74個、内側の立方体が10個あります。

外部の立方体の数が内部の立方体の数と等しくなるように、すべての直方体の寸法を指定します。

Gialmere

このような直方体は 20 個あります。
  1. 5×13×132
  2. 5×14×72
  3. 5×15×52
  4. 5×16×42
  5. 5×17×36
  6. 5×18×32
  7. 5×20×27
  8. 5×22×24
  9. 6×9×56
  10. 6×10×32
  11. 6×11×24
  12. 6×12×20
  13. 6×14×16
  14. 7×7×100
  15. 7×8×30
  16. 7×9×20
  17. 7×10×16
  18. 8×8×18
  19. 8×9×14
  20. 8×10×12

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

0 < a < bとします。a^bとb^aのどちらがより大きいでしょうか？

匿名

答えは具体的には a と b によって異なりますが、2 つの経験則でほとんどの状況に対応できます。

a > e なら a^b > b^a

b < eの場合、a^b < b^a

a < e かつ b > e の場合、判定するには情報が不十分です。

解決策はこちら（PDF）です。

手榴弾を底なしの穴に投げ込むと、平均6秒後に爆発します。爆発までの時間は記憶されない性質を持ち、ある瞬間の爆発確率は常に一定であり、ピンが抜かれてからの経過時間には依存しません。言い換えれば、手榴弾の寿命は指数分布に従います。加速度は毎秒32フィートと仮定します。

Ace2

1,152フィート

ここに私の完全な解決策（PDF）があります。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

利己的で完璧な論理家である二人の出場者がいるゲーム番組を考えてみましょう。ルールは次のとおりです。

  1. 司会者は2人の出場者の間のテーブルに100万ドルを置きます。
  2. 出場者Aは、2人の出場者の間でお金をどのように分配するかについて提案を求められます。
  3. 出場者 B は提案を受け入れるか拒否するかを尋ねられます。
  4. 出場者Bが提案を受け入れた場合、お金をそのように分配し、ゲームは終了します。
  5. 出場者 B が提案を拒否した場合、司会者は現在テーブルにある金額の 10% を削除します。
  6. 次に司会者は出場者 B に提案をするように求め、出場者 A にも同様にそれを受け入れるか拒否するかを選択する機会が与えられます。
  7. 出場者Aが提案を受け入れた場合、賞金はそのように分配され、ゲームは終了します。拒否した場合、ホストはテーブルに残っている金額の10%をさらにレーキで徴収します。その後、ステップ2に戻り、提案が受け入れられるまでこれを繰り返します。

問題は、出場者Aが最初のターンでお金の分配をどのように提案すべきかということです。

匿名

彼は、19分の10を自分のために取っておき、1ペニーを差し引いた金額をBに渡し、残りの19分の9と1ペニーをBに渡すことを提案するべきです。つまり、

答え: 526,315.78ドル
B: 473,684.22ドル

重要なのは、A が B をできるだけ無関心点に近づけることです。

ポットと他のプレイヤーの比率をrとしましょう。Bがオファーを受け入れた場合、r×1,000,000ドルを受け取ります。

Bがオファーを拒否した場合、司会者は10%の手数料を受け取ります。その後、Bはポジションアドバンテージを得て、出場者Aにrの分け前を提供し、1-rを自身で保持します。

r を解く...

r×1,000,000ドル = (1-r)×900,000ドル。
r×1,900,000ドル = 900,000ドル。
r = 900,000ドル/1,900,000ドル = 9/19。

AはBが全く無関心でいることを望んでいません。Bがランダムに選択して、ホストがポットを奪い取ってしまう可能性を恐れているからです。そこでAはBに1セント余分に賭け、(9/19) × 1,000,000ドル + 0.01ドル = 473,684.22ドルを提示すべきです。

答え: 526,315.78ドル
B: 473,684.22ドル

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

フォントルロイとサウスワースという二つの都市が、海峡を挟んで真向かいに位置しています。二つの都市の間を、2隻のフェリーが一日中往復しています。フェリーの速度はそれぞれ異なりますが、同時に出発します。

最初に渡るのはサウスワースから5マイルの地点です。2回目はフォントルロイから3マイルの地点です。荷物の積み下ろしに時間はないものと想定しますが、どちらもすぐにUターンします。また、両列車は直線で進むものと想定します。

二つの都市はどれくらい離れていますか？

匿名

12マイル

t 1 = 最初の交差点までの時間とする
t 2 = 2回目の交差点までの時間
r = フォントルロイを最初に出発するフェリーの速度とサウスワースを最初に出発するフェリーの速度の比。
c = 2つの都市間の水路の距離。

最初に横断する地点はサウスワースから5マイルの地点であることが分かっています。これを数式で表すと、次のようになります。

c-5 = r*t 1
5 = t 1

t 1 を等しくすると次のようになります。

c-5 = 5r、またはr = (c-5)/5

2回目の渡河地点はフォントルロイから3マイルの地点であることも分かっています。これを数式で表すと、次のようになります。

3c - 3 = r*t 2
c+3 = t 2

t 2 を等しくすると次のようになります。

2c - 3 = r*(c+3)

r=(c-5)/5を代入する

2c-3 = [(c-5)/5] * (c+3)
10c - 15 = c^2 - 2c - 15
c^2 - 12c = 0 c - 12 = 0 c = 12

つまり、水路の長さは12マイルです。

次の図で、青い領域の面積はどれくらいでしょうか?

匿名

答えについては下のボタンをクリックしてください。

1/2

これが私の解決策です（PDF）。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

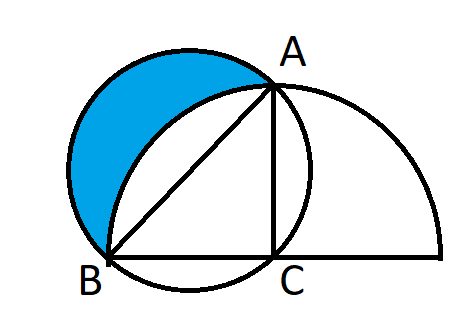
チェスのトーナメントでは、各出場者は他の出場者全員と対戦します。各出場者は、勝った試合ごとに1ポイント、引き分けの試合ごとに0.5ポイント、負けた試合ごとに0ポイントを獲得します。

トーナメントの終了時には、すべての競技者がそれぞれ異なるポイント数を獲得し、スコアランキングの最下位の競技者が上位 3 名の競技者をそれぞれ破ったことがわかります。

したがって、トーナメントに参加する競技者の最小人数は何人ですか?

Gialmere

13

プレイヤーの数をnとしましょう。

最下位のプレイヤーは、上位3人のプレイヤーに対して3勝しか挙げられず、それ以外の試合はすべて負けていると考えられます。つまり、3ポイント獲得です。

次に、ポイント順で後続のプレイヤーを、前のプレイヤーより0.5ポイント多く獲得する（順位付け）。つまり、最高位のプレイヤーのポイントは3+(n-1)/2となる。

3 と 3+(n-1)/2 を 1 ステップあたり 1/2 ポイントずつ加算すると、(((n+5)*(n+6)/2)-15)/2 になります。

n人のプレイヤーがプレイするゲームの総数はn*(n-1)/2で、全員が他のプレイヤーと1回ずつ対戦します。各ゲームで合計1ポイントが加算され、これは全プレイヤーの獲得ポイントの合計でもあります。

次にnについて解きます。

(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n^2 + 11n = 2n^2 - 2n
n + 11 = 2n-2
n=13

以下の表は、これがどのように起こるかを示しています。表の本体には、78試合すべての勝者が示されています。

以下の表は各プレイヤーのポイント数を示しています。

プレイヤー別合計ポイント

プレーヤーポイント
13 3
12 3.5
11 4
10 4.5
9 5
8 5.5
7 6
6 6.5
5 7
4 7.5
3 8
2 8.5
1 9

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

砲弾を積み重ねるには、エジプトのピラミッドのように底面が四角いピラミッドと、四面体を形成する三角形のピラミッドのどちらが効率的でしょうか?

匿名

読者にとって役立つと思われる数式をいくつか示します。

1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ... + n 2 = n*(n+1)*(2n+1)/6

1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6

私の回答と解決策については下にスクロールしてください。

「効率的」とは、砲弾間の無駄なスペースが最も少ないものを指していると思います。

物事を単純にするために、ピラミッドの体積を定義するには、ピラミッドの角にある球の中心を使います。そして、ピラミッドの底面の1辺にある砲弾の数をnとします。

まずは四角い底を持つピラミッドを見てみましょう。

ピラミッド全体の砲弾の数は、1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ... + n 2 = n*(n+1)*(2n+1)/6 です。

次に、底辺がnである四角錐の高さを求めましょう。図からわかるように、（正方形の底辺以外の）辺は正三角形です。したがって、斜高もnです。底辺の一方の角から反対側の角までの距離はn*sqrt(2)です。したがって、底辺の一方の角から底辺の中心までの距離はn*sqrt(2)/2です。高さをhとします。高さ、底辺の一方の角から底辺の中心までの距離、そして斜高によって形成される直角三角形を考えます。

h 2 + (n*sqrt(2)/2) 2 = n 2
h = n*sqrt(2)/2 です。

ピラミッドの体積は底辺×高さ÷3であることを思い出してください。つまり、ピラミッドの体積は次のようになります。

n 2 * n* sqrt(2)/2 * (1/3) = n 3 *sqrt(2)/6。

ボールの体積に対する比率は[n*(n+1)*(2n+1)/6] / [n 3 *sqrt(2)/6] = sqrt(2)*n*(n+1)*(2n+1)/(2*n 3 ) = sqrt(2)*(n+1)*(2n+1)/(2*n 2 )となる。

次に三角形の底面を持つピラミッドを見てみましょう。

ピラミッド全体の砲弾の数は、1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6 です。

次に、底面積を求めましょう。30-60-90の三角形の辺は、1/2、sqrt(3)/2、1に比例することを思い出してください。これより、辺がnの正三角形の高さはn*sqrt(3)/2であることが容易にわかります。つまり、底面積はn 2 *sqrt(3)/4となります。

底辺の角から底辺の中心までの距離は、平方根(3)/3です。これとピラミッドの斜辺の高さ1から、ピタゴラス定理を用いてピラミッドの高さを平方根(6)/3と求めることができます。

ピラミッドの体積は、底辺*高さ/3 = (n 2 *sqrt(3)/4) * (n*sqrt(6)/3) * (1/3) = n 3 *sqrt(18)/36 = n 3 *sqrt(2)/12 と求められます。

ボールの体積に対する比率は[n*(n+1)*(n+2)/6] / [n 3 *sqrt(2)/12] = sqrt(2)*n*(n+1)*(2n+1)/(2*n 3 ) = sqrt(2)*(n+1)*(n+2)/n 2となる。

ボールと体積の比率の比較は次のとおりです。

  • 平方底: sqrt(2)*(n+1)*(2n+1)/(2*n 2 )
  • 三角形の底辺: sqrt(2)*(n+1)*(n+2)/n 2

両方の比率をsqrt(2)*(n+1)/n 2で割ります。

  • 平方底: (2n+1)/2 = n + 0.5
  • 三角形の底辺: n+2

nが大きくなるにつれて、どちらのピラミッドでも、砲弾の数と体積の比率はnに近づきます。つまり、砲弾の数が多いほど、効率は等しくなります。

砲弾の体積を考えると、両方のピラミッドの効率は、砲弾の体積と全体の体積の比として定義され、π*sqrt(2)/6 =~ 約 74.05% に近づきます。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

任意の大きな数について、その数の近くにある素数間の平均距離はどれくらいでしょうか？また、その数より小さい素数はいくつあるでしょうか？

匿名

任意の大きな数nの近傍における素数間の平均距離の非常に良い推定値はln(n)です。この推定値の精度の高さは注目に値します。

証拠として、次の表は最初の1500万個の素数の範囲を100万個ずつのグループに分けて示しています。表は、素数間の範囲内の平均距離と、平均距離の推定値を示しています。推定値は、範囲内の最大素数と最小素数の平均の自然対数です。例えば、15番目の100万個の素数グループの場合、ln((256,203,221+275,604,541)/2)となります。

素数間の平均距離

ファーストプライム
範囲内		ラストプライム
範囲内		素数
範囲内		平均距離見積もり
2 15,485,863 1,000,000 15.485861 15.86229105
15,485,867 32,452,843 1,000,000 16.966976 16.9922867
32,452,867 49,979,687 1,000,000 17.52682 17.53434381
49,979,693 67,867,967 1,000,000 17.888274 17.89175615
67,867,979 86,028,121 1,000,000 18.160142 18.15864108
86,028,157 104,395,301 1,000,000 18.367144 18.3716137
104,395,303 1億2294万9823 1,000,000 18.55452 18.54883262
1億2294万9829円1億4165万939円1,000,000 18.70111 18.70058553
1億4165万9630円1億6048万1183 1,000,000 18.83022 18.83322787
1億6048万1219円1億7942万4673 1,000,000 18.943454 18.95103217
1億7942万4691 1億9849万1317円1,000,000 19.066626 19.05703535
1億9849万1329円2億1764万5177円1,000,000 19.153848 19.15337672
2億1764万5199円2億3,688万7,691 1,000,000 19.242492 19.24163365
2億3,688万7,699 2億5,620万3,161 1,000,000 19.315462 19.32305683
2億5,620万3,221 2億7560万4541 1,000,000 19.40132 19.39864545

出典: Prime Pages のThe Gaps Between Primes 。

任意の数における素数の個数を求めるには、まず平均距離の推定値ln(n)を積分することから始めます。これにより、任意の数nまでの素数間の平均距離の合計が得られます。

f(n)=ln(n)の積分はいくらでしょうか？部分積分から次のことがわかります。

f(n)*g'(n) dnの積分 = f(n)*g(n) - (f'(n)*g(n)) dnの積分

f(n)=ln(n)、g'(n)=1とします。すると、f'(n)=1/n、g(n)=nとなります。したがって、ln(n)の積分は、ln(n)*n - ((1/n)*n)の積分 = ln(n)*n - n = n*(ln(n)-1)となります。

n*(ln(n)-1)をnで割ると、2からnまでの範囲における素数間の平均距離が得られます。これはln(n)-1です。

n をこの素数間の平均距離で割ると、n 未満の素数の平均数が得られ、これは n/(ln(n)-1) に等しくなります。

証拠として、以下の表は様々な大きな数における素数の個数と推定値を示しています。Excelの精度は15桁までしかなく、ご容赦ください。誰か、もっと高い精度に対応できるスプレッドシートを作ってください。

素数間の平均距離

n n以下の素数n/(ln(n)-1)
10 4 8
100 25 28
1,000 168 169
10,000 1,229 1,218
10万9,592 9,512
1,000,000 78,498 78,030
10,000,000 664,579 661,459
1億5,761,455 5,740,304
1,000,000,000 50,847,534 50,701,542
10,000,000,000 4億5,505万2,511 454,011,971
100,000,000,000 4,118,054,813 4,110,416,301
1,000,000,000,000 37,607,912,018 37,550,193,650
10,000,000,000,000 346,065,536,839 345,618,860,221
100,000,000,000,000 3,204,941,750,802 3,201,414,635,781
1,000,000,000,000,000 29,844,570,422,669 29,816,233,849,001
10,000,000,000,000,000 279,238,341,033,925 279,007,258,230,820
100,000,000,000,000,000 2,623,557,157,654,230 2,621,647,966,812,030
1,000,000,000,000,000,000 24,739,954,287,740,800 24,723,998,785,920,000
10,000,000,000,000,000,000 234,057,667,276,344,000 233,922,961,602,470,000
100,000,000,000,000,000,000 2,220,819,602,560,910,000 2,219,671,974,013,730,000
1,000,000,000,000,000,000,000 21,127,269,486,018,700,000 21,117,412,262,910,000,000
10,000,000,000,000,000,000,000 201,467,286,689,315,000,000 201,381,995,844,660,000,000
100,000,000,000,000,000,000,000 1,925,320,391,606,800,000,000 1,924,577,459,166,810,000,000
1,000,000,000,000,000,000,000,000 18,435,599,767,349,200,000,000 18,429,088,896,563,900,000,000
10,000,000,000,000,000,000,000,000 176,846,309,399,143,000,000,000 176,788,931,049,964,000,000,000

出典: Prime Pages の「素数はいくつあるか? 」

七角

上の図は、辺の長さが 1 の九角形です。

AB+AC と AE ではどちらが多いでしょうか?

この問題はMensa Bulletin 2021 年 3 月号から抜粋したものです。

匿名

両者は同等です。

この問題に対する私の解決策は次のとおりです。(PDF)

答えが整数であると仮定して、3 桁または 4 桁の数字の平方根を簡単に求めるにはどうすればよいでしょうか。

匿名

次の表は、0 から 9 までの数字、それぞれの数字の平方、およびその平方の最後の桁を示しています。

平方数の最後の桁

オリジナル
番号		四角最後の桁
スクエアの
0 0 0
1 1 1
2 4 4
3 9 9
4 16 6
5 25 5
6 36 6
7 49 9
8 64 4
9 81 1

偶数平方の数は必ず0、1、4、5、6、または9で終わることに注意してください。これはすべての平方数に当てはまります。これは、元の数の最後の桁が平方数の最後の桁を決定するためです。

ステップ1：平方根の最後の桁に基づいて、以下の表を使って平方根の最後の桁を絞り込むことができます。例えば、平方根が2809の場合、平方根の最後の桁は3または7です。

元の番号の最後の桁

最後の桁
平方根の		最後の桁
スクエアの
0 0
1 1または9
4 2または8
5 5
6 4または6
9 3または7

ステップ2：次に、元の数字の右2桁を切り捨てます。例えば、元の数字が2809だった場合は、28を使用します。

ステップ3：ステップ2の結果以下の最小の平方数を見つけます。そして、その平方数の平方根を取ります。例えば、28より小さい最小の平方数は25です。25の平方根を取ると5になります。

100 までの平方数を記憶していない場合は、次の表を使用できます。

平方根の最初の部分

ステップ2ステップ3
1から3 1
4～8 2
9～15歳3
16～24歳4
25～35歳5
36から48 6
49から63 7
64から80 8
81から99 9

ステップ 4: ステップ 1 の結果が 0 または 5 の場合は、それをステップ 3 の結果の後に置いて完了です。

それ以外の場合、a = ステップ3の結果とします。b = a×(a+1)とします。例えば、ステップ3の結果が5の場合、b = 5×6 = 30となります。

ステップ 5: b < a の場合、平方根の最後の桁はステップ 1 で得られた可能性のうち小さい方になります。それ以外の場合、b >= a の場合は、2 つの可能性のうち大きい方になります。

ステップ 6: 平方根を求めるには、ステップ 3 の結果を取得し、それにステップ 5 の結果を加算します。つまり、10 × (ステップ 3) + ステップ 5 となります。

いくつかの例を見てみましょう。

256 の平方根を求めます。

  • ステップ 1: 平方根の最後の桁は 4 または 6 です。
  • ステップ 2: 最後の 2 桁を削除すると、2 になります。
  • ステップ 3: 2 以下の最小の平方数は 1 です。1 の平方根は 1 です。
  • ステップ4: 1*(1+1) = 2。
  • ステップ 5: ステップ 4 の結果はステップ 2 の結果と等しいので、ステップ 1 のオプションのうち大きい方を最後の桁、つまり 6 として使用します。
  • ステップ 6: 平方根は、ステップ 5 の結果を 3 の結果に加算したもので、1 & 6 = 16 になります。

1369 の平方根を求めます。

  • ステップ 1: 平方根の最後の桁は 3 または 7 です。
  • ステップ 2: 最後の 2 桁を削除すると、13 になります。
  • ステップ 3: 13 以下の最小の平方数は 9 です。9 の平方根は 3 です。
  • ステップ4: 3*(1+3) = 12。
  • ステップ 5: ステップ 2 の結果はステップ 4 の結果よりも大きいため、ステップ 1 のオプションのうち大きい方を最後の数字として使用します (つまり、7)。
  • ステップ 6: 平方根は、ステップ 5 の結果を 3 に加えた結果であり、3 & 7 = 37 になります。

2704 の平方根を求めます。

  • ステップ 1: 平方根の最後の桁は 2 または 8 です。
  • ステップ 2: 最後の 2 桁を削除すると、27 になります。
  • ステップ 3: 27 以下の最小の平方数は 25 です。25 の平方根は 5 です。
  • ステップ4: 5*(1+5) = 60。
  • ステップ 5: ステップ 2 の結果はステップ 4 の結果より小さいため、ステップ 1 のオプションのうち小さい方を最後の桁として、つまり 2 を使用します。
  • ステップ 6: 平方根は、ステップ 5 の結果を 3 の結果に加算したもので、5 & 2 = 52 になります。

5625 の平方根を求めます。

  • ステップ 1: 平方根の最後の桁は 5 です。
  • ステップ 2: 最後の 2 桁を削除すると、56 になります。
  • ステップ 3: 56 以下の最小の平方数は 49 です。49 の平方根は 7 です。
  • ステップ4: ステップ1の結果は0または5なので、答えはステップ3の結果にステップ1の結果を加えたものになります: 7 & 5 = 75

6561 の平方根を求めます。

  • ステップ 1: 最後の数字は 1 または 9 です。
  • ステップ 2: 最後の 2 桁を削除すると、65 になります。
  • ステップ 3: 65 以下の最小の平方数は 64 です。64 の平方根は 8 です。
  • ステップ4: 8*(1+8) = 72。
  • ステップ 5: ステップ 2 の結果はステップ 4 の結果より小さいため、ステップ 1 のオプションのうち小さい方を最後の桁、つまり 1 として使用します。
  • ステップ 6: 平方根は、ステップ 5 の結果を 3 の結果に加算したもので、8 & 1 = 81 になります。

この方法のデモはYouTubeでご覧いただけます。

辺の長さが1の正五角形の面積はいくらですか？

匿名

答えについては下のボックスをクリックしてください。

(sqrt(5)/4)*sqrt(5+2*sqrt(5)) = 約1.72047740058897。

ヒントについては下のボックスをクリックしてください。

[ネタバレ=ヒント]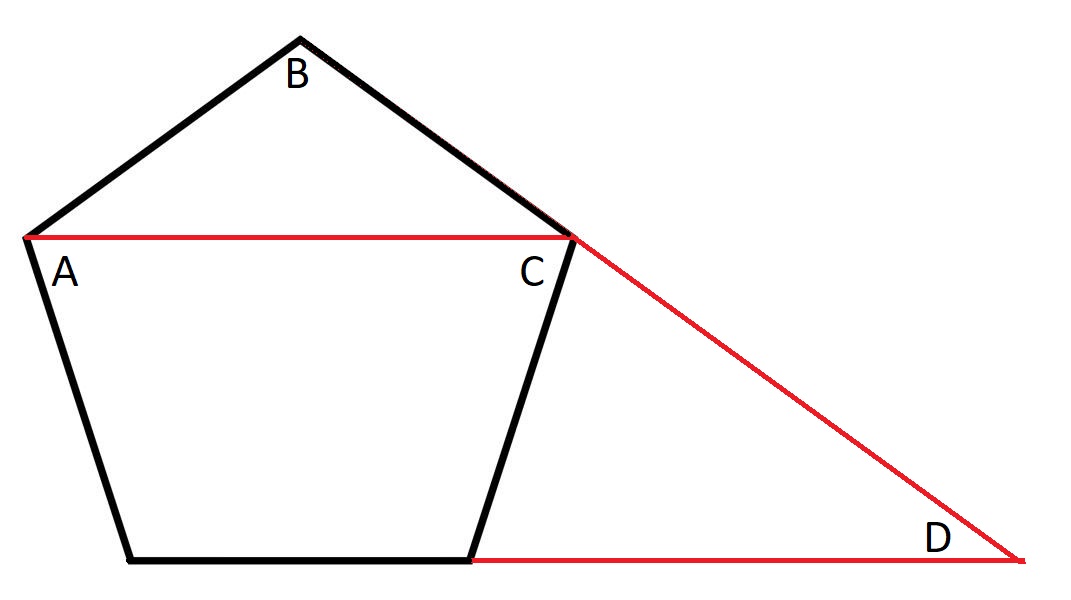

ペンタゴンのヒント

上の画像を考えてみましょう。AC = CD です。

[/spoiler]

これが私の解決策です（PDF）

風のない日、チャーリーはカヌーで川へ行き、上流へ漕ぎ出しました。彼は常に同じ速度で漕ぎ続けていました（つまり、流れを無視すれば、常に同じ速度で進むことになります）。カヌーを漕ぎ出してから1マイル（約1.6キロメートル）ほどの地点で、彼の帽子が川に落ちてしまいました。それから10分後、彼は帽子がないことに気づき、すぐにUターンして下流へ向かいました。チャーリーはカヌーを漕ぎ出したのと同じ場所で、彼の帽子に追いつきました。

電流の速さはどのくらいですか？

匿名

答えについては下のボタンをクリックしてください。

時速3マイル。

これが私の解決策です（PDF）。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

次の質問はバーベットに関するものです。任意の紙幣にランダムに割り振られた米国の通し番号が使用されます。プレイヤーは0から9までの任意の3桁の数字を選択します。3桁の数字は必ず異なるものでなければなりません。勝敗は、選択した3桁の数字が通し番号に少なくとも1回出現する数によって決まります。

例えば、プレイヤーの選択が7-0-2で、シリアルナンバーが22227755の場合、一致は2つあります。2と7が複数回一致しても問題ありません。

提示されたオッズは次のとおりです:

  • 3試合：5対1
  • 2試合：1対1
  • 1試合：9対5
  • 0試合：15対1

各ベットの勝率とハウスエッジはどれくらいですか?

匿名

以下の表は、各ベットにおける当選組み合わせの数、当選確率、ハウスエッジを示しています。右の列は、ハウスエッジが7.4%から8.5%の範囲であることを示しています。

シリアルナンバーベット

マッチ支払う組み合わせ確率ハウスエッジ
3 5 15,426,684 0.154267 0.074399
2 1 45,771,270 0.457713 0.084575
1 1.8 33,037,245 0.330372 0.074957
0 15 5,764,801 0.057648 0.077632

1 から 9 までの各数字をそれぞれ 1 回ずつ使用して、分子に 1 桁、分母に 2 桁の分数を 3 つ作成します。3 つの分数の和は 1 になります。

たとえば、8/16 + 9/27 + 3/24 は、合計が 1 ではなく 23/24 になることを除いて、すべての条件を満たします。

Gialmere

5/34 + 7/68 + 9/12

答えを見つけるには、permut(9,3)*permut(6,3)*permut(3,3)/fact(3) = 60,480通りの可能な順列を並べる必要があります。少なくとも1時間は試行錯誤しましたが、解は見つかりませんでした。

そこで、9桁の数字をfact(9) = 362,880通りの並び替え方法すべてを試すプログラムを書き、すべてテストしました。難しいのは、9桁の数字をあらゆる順序で並べる方法をすべて試すことでした。ここでは、辞書式ソートを使ってその方法を説明します。

  1. 9 つの要素すべてを、最小から最大の順に配列します。
  2. 配列内の最後の要素のうち、次の要素よりも大きい要素を探します。見つからない場合は、プログラムを終了します。
  3. 手順 2 の次の要素から始めて、手順 2 よりも大きい配列の最後の要素を検索します。
  4. 手順 2 と 3 の配列内の要素を交換します。
  5. 手順 2 の次の配列の要素を最後まで逆にします。
  6. ステップ2に戻る

このプロセスに従うと、3 つの分数を順序付ける 6 つの方法すべてに対して 1 回ずつ、合計 6 回、正しい答えが見つかります。

私は、1 から 9 までのすべての数字を辞書式順序で並べ替え、それぞれが解であるかどうかをテストする次のコードを作成しました。


void three_fraction(void)
{
 int i、x_max、y_max、temp_array[100]、hold、pt;
 int lex_array[] = { 1,2,3,4,5,6,7,8,9 };
 int num_elements = sizeof(lex_array) / sizeof(lex_array[0]);
 整数カウント = 0;
 ブール停止 = false;
 ダブルtot3;
 cerr << "要素数 =\t" << num_elements << "\n";
 する
 {
  カウント++;
  tot3 = (double)lex_array[0] / (double)(10 * lex_array[1] + lex_array[2]);
  tot3 += (double)lex_array[3] / (double)(10 * lex_array[4] + lex_array[5]);
  tot3 += (double)lex_array[6] / (double)(10 * lex_array[7] + lex_array[8]); 
  tot3 == 1.0の場合
  {
   cerr << count << "\t";
   cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
   cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
   cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
  } 
  x_max = -1;
  (i = 0; i < (要素数 - 1); i++) の場合
  {
   (lex_array[i] < lex_array[i + 1]) の場合
    x_max = i;
  }
  (x_max >= 0)の場合
  {
   y_max = 0;
   (i = x_max + 1; i < num_elements; i++) の場合
   {
    lex_array[x_max] < lex_array[i] の場合
     y_max = i;
   }
   ホールド = lex_array[x_max];
   lex_array[x_max] = lex_array[y_max];
   lex_array[y_max] = 保持;
   if (x_max + 1 < num_elements - 1) // 逆順
   {
    (i = x_max + 1; i < num_elements; i++) の場合
    {
     temp_array[i] = lex_array[i];
    }
    pt = 0;
    (i = x_max + 1; i < num_elements; i++) の場合
    {
     lex_array[i] = temp_array[要素数 - 1 - pt];
     pt++;
    }
   }
  }
  それ以外
   停止 = true;
 } while (stop == false);
}

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

ある男が10ガロンのワイン樽と水差しを持っていました。ある日、彼は水差し一杯のワインを汲み上げ、樽に水を注ぎました。その後、ワインと水が完全に混ざり合ったところで、彼はもう一杯の水差しを汲み上げ、再び樽に水を注ぎました。すると、樽にはワインと水が同量ずつ入っていました。

水差しの容量はどれくらいでしたか？

Gialmere

10-5*sqrt(2) =~ 2.9289ガロン

j を水差しの容積とします。

最初に水差しにワインを注ぎ込んだ後、水差しには10-jガロンのワインが残っていました。ワインを水に置き換えた後、樽全体に対するワインの比率は(10-j)/10でした。

ジョッキが薄めたワインをすくい取った後、樽の中には10ガロン（約4.7リットル）の薄めたワインが残っていました。薄めたワインに含まれる純ワインの量は、次のように表すことができます。

(10-j)*((10-j)/10) = 5

(10-j)^2 = 50

j^2 - 20j + 100 = 50

j^2 - 20j + 50 = 0

j = (20 +/- 平方根(400-200))/2

j = (20 +/- 10*sqrt(2))/2

j = 10 +/- 5*sqrt(2)

水差しは樽より大きくすることはできないので、負の符号を使用する必要があります。

j = 10 - 5*sqrt(2) =~ 約 2.92893218813452 ガロン。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

感謝祭を祝うため、あなたと19人の数学者が円形のテーブルに着席しています。テーブルの全員がクランベリーソースを頼もうとしており、たまたま目の前にクランベリーソースがあります。

まず、自分でソースを取ります。そして、ソースを円を描くように回すのではなく、自分のすぐ左か右に座っている人にランダムに渡します。相手も同じように、自分の左か右に座っている人にランダムに渡します。これを繰り返し、全員がクランベリーソースを受け取るまで続けます。

円の中にいる 20 人のうち、最後にクランベリー ソースを受け取る可能性が最も高いのは誰でしょうか?

Gialmere

他の人もクランベリーソースを最後にもらう可能性は平等にあります。

数学者の一人に G という名前をつけましょう。G が最後になるには、次の 2 つの条件を満たす必要があります。

  1. クランベリーはまず G のどちらかの隣に到達する必要があります。
  2. クランベリーは G に到達することなく、反対方向に 19 位置移動する必要があります。

最後になるには、クランベリーは最終的にどちらかの隣の人に届く必要があります。つまり、その確率は100%です。

すると、2番目の部分の確率が何であれ、それは各人にとって同じです。つまり、各人が最後になる確率は等しいのです。

もし説明が分かりにくかったら、Gialmereはこの問題をfivethirtyeight.comから入手しました。こちらで解決策が説明されています。「先週のRiddler Classicの解答」までスクロールダウンしてください。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

こちらがThe Riddlerからのもう一つのパズルです。

袋の中にビー玉が100個入っています。それぞれのビー玉は赤、青、緑のいずれかです。袋からビー玉を3個取り出すと、各色のビー玉が1個ずつ出る確率は20%です。袋の中には各色のビー玉がいくつ入っていますか？ビー玉が交換ありで取り出されるか、交換なしで取り出されるかは特に言及していません。

Gialmere

赤、青、緑のビー玉の数はそれぞれ21個、35個、44個で、順番は問いません。袋から取り出す際は、取り戻さずにそのまま取り出します。

「復元あり」の仮定のもとで計算してみましょう。r、b、gをそれぞれ赤、青、緑のビー玉の数とします。すると、各色のビー玉が1つずつ出る確率は6*(r/100)*(b/100)*(g/100)となります。これを0.2とすると、以下の式が成り立ちます。

6*(r/100)*(b/100)*(g/100) = 0.2
6*r*b*g = 200000 ​

6は200,000を割り切れません。したがって、r*b*g = 33333.333...の整数解は存在しません。したがって、置換による抽出は除外できます。

次に、「無復元」仮定を試してみましょう。この場合、各色を1枚ずつ引く確率はr*b*g/combin(100,3) = 0.2です。これを解いてみましょう…

r*b*g/161700 = 0.2
r*b*g = 32340

32340 を素因数分解すると、2*2*3*5*7*7*11 になります。

r+b+g=100 を維持しながら、これらの因数を r、b、g に分配する必要があります。例えば、次のようにしてみましょう。

r = 2*3*5 = 30
b = 2*11 = 22
グラム = 7 * 7 = 49

これらは素因数をすべて正しく使用していますが、r+b+g = 101 なので有効な解ではありません。

残念ながら、r、b、g の値が任意の順序で 21、35、44 になるという解を得るには、力ずくのループ プログラムを書く必要がありました。

次の質問は、Riddler Express のご厚意により寄せられたものです。

NFLのルールを前提に考えてみましょう。次の状況を考えてみましょう。

  • レッドチームは試合終盤で14点差をつけられている
  • レッドチームはあと2回ボールを保持します
  • 青チームはこれ以上の所有権を持たない
  • フィールドゴールとセーフティは無視しましょう。レッドチームが勝利するには2回のタッチダウンが必要です。
  • 試合が延長戦に突入した場合、両チームの勝率は50%となります。引き分けで終わることはありません。
  • タッチダウン後に1ポイントキックを成功させる確率は100%です。
  • 2 ポイントコンバージョンを達成する確率は p です。

p の値がどのくらいのとき、赤チームは最初のタッチダウン (現在 8 点差) の後にキックして 2 ポイント コンバージョンを狙うことに無関心になるでしょうか。

匿名

(3-sqrt(2))/2 = 約 0.381966011250105

2 ポイント コンバージョンを狙うかキックするかの間の無差別点を p とします。

最初の 2 ポイント コンバージョンの試みが成功した場合、赤チームは 2 回目にボールを蹴って勝つことができます。

最初の 2 ポイント コンバージョンの試みが失敗した場合、赤チームは 2 回目のタッチダウン後にもう一度試み、延長戦で試合に勝たなければなりません。

最初のタッチダウン後に2ポイントコンバージョンを狙う場合の勝率はp + (1-p)*p/2です。これを最初のタッチダウン後にキックで勝てる確率50%と等しくし、pについて解きます。

p + (1-p)*p/2 = 1/2
2p + (1-p)*p = 1
3p - p^2 = 1
p^2 - 3p + 1 = 0

二次方程式の公式を使ってpを解きます。

p = (3 +/- 平方根(5))/2

pを0と1の間に保つために負のオプションを選択し、p = (3-sqrt(2))/2 = apx. 0.381966011250105を得る。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

前回の「Ask the Wizard」コラムで、2つのサイコロを2回連続で振って合計12になるために必要なサイコロの目数について質問されました。関連して、フォーラムでクラップスのテーブルで18回連続（合計11）のサイコロの目を見たという投稿を見かけました。そうなるために必要なサイコロの目数はどれくらいでしょうか？

匿名

41660902667961039785742

これが私の解決策です（PDF）。

この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

WizCalcの助けを借りて正確な答えが見つかりました。

草地は半径100mの円状で、円形の柵で囲まれています。柵の固定された一点に、ヤギがフックに鎖で繋がれています。ヤギが太りすぎないように、農家はヤギが草地の半分までしか届かないようにしたいと考えています。鎖の長さはどのくらいにすべきでしょうか？

例として、円は草原を表しています。Sは草原の端に鎖が張られている場所を表しています。円の黄色い部分はヤギが届く範囲です。緑の部分は鎖が届かない範囲です。目標は、緑と黄色の部分が等しくなるように鎖を適切な距離にすることです。

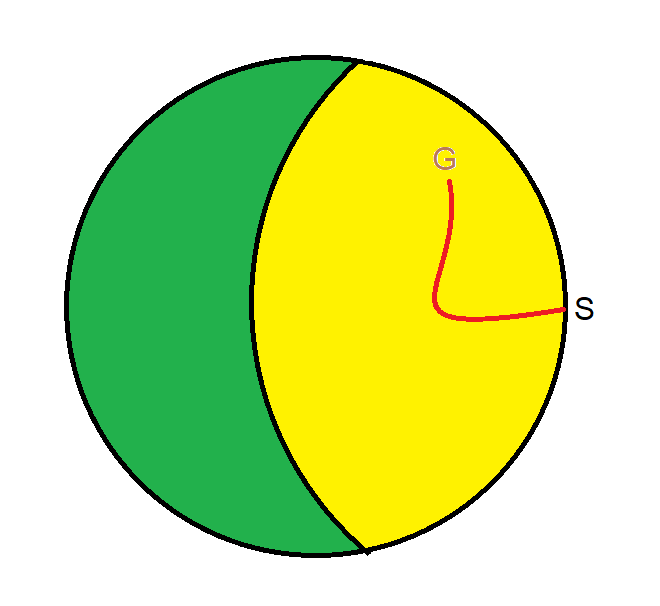
ヤギの質問

Gialmere

115.87286メートル。

この問題を解く際には次の図を参照してください。

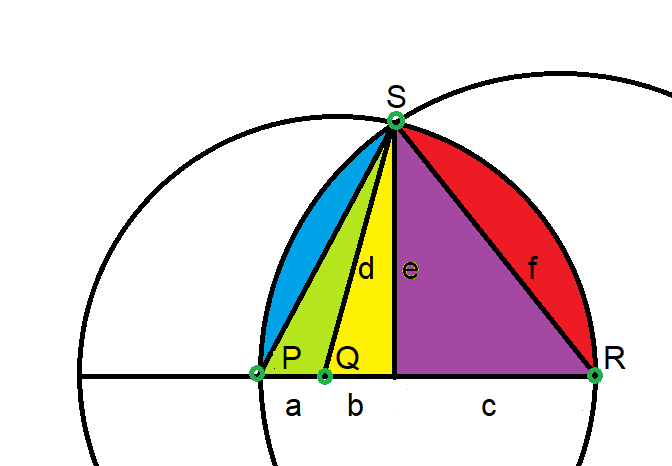
ヤギパズル

点Qは草地の円の中心です。ヤギの鎖は点Rに繋がれています。ヤギは線PRの下の鏡像を含む、すべての色の領域に到達できます。

草の円の半径は 100 なので、b+c = d = 100 となります。

これを解くには、すべてをbで定義します。そして、ヤギが草の半分を食べられるという望ましい結果が得られるまで、bを調整していきます。

まず、eをbについて解いてみましょう。b、d、eの3辺を持つ三角形を見て、ピタゴラスの定理を使います。

b^2 + e^2 = d^2
b^2 + e^2 = 10000
e = 平方根(10000 - b^2)

次に、f を b について解いてみましょう。b+c=100 なので、c=100-b であることを覚えておいてください。ピタゴラスの定理を使って：

c^2 + e^2 = f^2
(100-b)^2 + (10000 - b^2) = f^2
f^2 = 10000 - 200b + b^2 + 10000 - b^2
f^2 = 20000 - 200b
f^2 = 100*(200 - 2b)
f = 10*sqrt(200-2b)

次に三角形QRSの面積を求めましょう。

QRS = (1/2)*100*e = 50*sqrt(10000 - b^2)

次に、角度 SQR で切り取られた草地のスライスの面積を求めましょう。

tan(SQR) = e/b = sqrt(10000-b^2)/b です。

スライス SQR = atan(sqrt(10000-b^2)/b)

赤い領域は、スライス SQR から三角形 QRS を引いた値 = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2) に等しくなります。

次に、青 + 緑 + 黄 + 紫の領域を見つけましょう。そのためには、QRS角を見つける必要があります。

tan(QRS) = e/c = sqrt(10000-b^2)/(100-b)

角度 QRS = atan(sqrt(10000-b^2)/(100-b))。

これに赤い領域を加えると、ヤギが食べることができる総面積の半分になります。

atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2)。

これを 2 倍にして、PR 線の下の部分の合計面積を求めます。

2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2)。

草地の総面積は10,000*piです。

では、b を調整して、ヤギが食べられる面積が 5,000*π になるまで計算してみましょう。Excel の goalseek 関数はこのような問題に最適です。スプレッドシートが登場する前は、どうやって物事をこなしていたのか、私には全く理解できません。

この方法を使用すると、b = 32.867402 であることがわかります。

そこから、f = チェーンの長さ = 115.8728598 メートルが得られます。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

Wordleで最初にお勧めする単語は何ですか?

匿名

その答えを得るために、私はまず、許可されている Wordle のソリューションのリストに基づいて、各位置における各文字の頻度を調べました。

Wordleにおける文字の頻度

手紙ポジション1ポジション2ポジション3ポジション4ポジション5合計
あ141 304 307 163 64 979
B 173 16 57 24 11 281
C 198 40 56 152 31 477
D 111 20 75 69 118 393
E 72 242 177 318 424 1233
F 136 8 25 35 26 230
G 115 12 67 76 41 311
H 69 144 9 28 139 389
私34 202 266 158 11 671
J 20 2 3 2 0 27
K 20 10 12 55 113 210
L 88 201 112 162 156 719
M 107 38 61 68 42 316
北37 87 139 182 130 575
お41 279 244 132 58 754
P 142 61 58 50 56 367
質問23 5 1 0 0 29
R 105 267 163 152 212 899
S 366 16 80 171 36 669
T 149 77 111 139 253 729
あなた33 186 165 82 1 467
V 43 15 49 46 0 153
W 83 44 26 25 17 195
X 0 14 12 3 8 37
はい6 23 29 3 364 425
Z 3 2 11 20 4 40

次に、Wordleの解答リストにある5つの異なる文字を持つすべての単語を調べ、上記の文字頻度表に従って採点しました。正しい位置で一致したものには2点、間違った位置で一致したものには1点を付与しました。その後、リストを並べ替えました。結果は以下のとおりです。

Wordleで使える最高の単語集

<!--/ボックスタイトル-->
中央揃え">ポイント
ランク言葉
1見詰める5835
2立ち上がった5781
3スレート5766
4上げる5721
5立ち上がれ5720
6より健全な5694
7スネア5691
8激怒5682
9古くなった5665
10クレート5652
11トレース5616
12後で5592
13共有5562
14店5547
15怖がらせる5546
16アルター5542
17クレーン5541
18警告5483
19涙目5479
20ソテー5475
21ケータリング5460
22スペア5457
23一人で5452
24貿易5449
25いびき5403
26格子5403
27シェール5392
28少しでも5390
29ストール5377
30規模5376
31反応する5376
32ブレア5368
33解析5351
34グレア5340
35償う5338
36学ぶ5324
37早い5320
38傾いた5307
39より淡い5285
40フレア5280
41通路5280
42海岸5274
43窃盗5268
44トライス5267
45スコア5258
46クリア5258
47クローン5253
48石5253
49心臓5252
50敗者5251
51テーパー5248
52ヘイター5243
53リレー5241
54皿5240
55崇拝する5239
56ソース5236
57より安全5235
58エイリアン5233
59カースト5232
60剪断5231
61ベーラー5230
62サイレン5226
63カヌー5215
64シャイア5213
65腎臓5210
66層5206
67テイマー5200
68大きい5196
69パール5196
70ルート5194
71ブレース5192
72スライス5178
73ステージ5171
74散文5170
75胞子5169
76ラウズ5166
77グレース5164
78太陽5152
79スイート5150
80ロースト5145
81ラガー5130
82飛行機5129
83クリート5129
84配られた5128
85槍5126
86素晴らしい5126
87エイダー5123
88比喩5116
89尖塔5108
90トレッド5107
91奴隷5097
92近い5090
93ランス5090
94リンス5088
95原因5087
96うつ伏せ5087
97ドローン5082
98ノイズ5079
99クレスト5073
100しらふ5068

ということで、私がお勧めする最初の言葉は「STARE」です。

i^iとは何ですか

Aidan

e^(-pi/2) =~ 0.20788。

これが私の解決策です（PDF）。

普通の6面ダイス2個を使うゲームをしたいと思っています。残念ながら、ダイスを失くしてしまいました。しかし、9枚のインデックスカードがあり、好きなように印を付けることができます。プレイヤーは9枚のインデックスカードからランダムに2枚を選び、その合計を求めます。

Gialmere

カードの値は整数である必要はありません。

カードに次のようにマークを付けます。

1 @ 0.5
1 @ 1.5
2 @ 2.5
1 @ 3.5
2 @ 4.5
1 @ 5.5
1 @ 6.5

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

公平なコインを投げると、表向きに出た面が表向きになる確率が高くなるというのは本当ですか?

匿名

証拠はこれが真実であることを示しています!

スタンフォード大学のペルシ・ディアコニスとスーザン・ホームズは、1万回のコイン投げを記録しました。コインは50.8%の確率で、投げたときと同じ面を上にして着地しました（出典：アメリカ数学会のニュースレター「What's Happening in the Mathematical Sciences」に掲載されている 「The Fifty-one Percent Solution 」）。この比率以上になる確率は5.48%です。

これを数学的に証明するために、コインの実際の回転数はポアソン分布に従うと仮定しました。より具体的には、平均回転数がmの場合、ちょうどn回回転する確率はexp(-m)*m^n/n!です。ポアソン分布を説明するために、次のグラフは平均10が与えられた場合に、0から25回回転する確率を示しています。

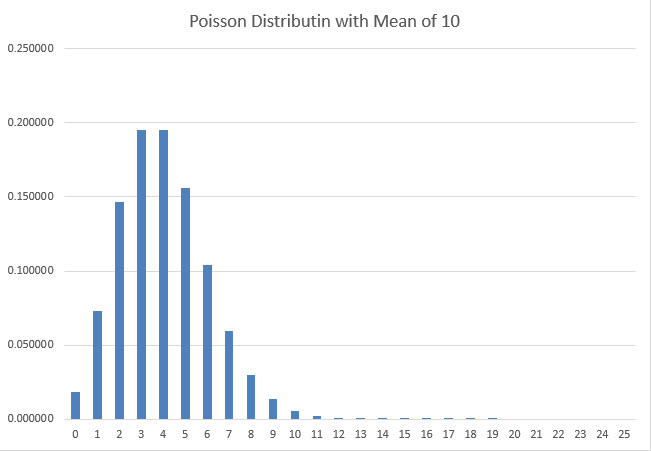
私がポアソン仮定を選択した理由は、十分に大きな平均値に対してほぼベル曲線の形状に従い、実際の結果がゼロを下回ることはないからです。

次に、半回転の回数が偶数回（開始時と同じ面が上を向いて着地する）となる確率を、様々な半回転の平均について計算しました。以下の表は、平均0.5～5.0の場合の結果を示しています。

偶数回転と奇数回転の確率

ミーン・レボリューションズ合計奇数合計
0.5 0.567667642 0.432332358
1 0.509157819 0.490842181
1.5 0.501239376 0.498760624
2 0.500167731 0.499832269
2.5 0.500022700 0.499977300
3 0.500003072 0.499996928
3.5 0.500000416 0.499999584
4 0.500000056 0.499999944
4.5 0.500000008 0.499999992
5 0.500000001 0.499999999

そこで、なぜ偶数の確率が常に50%より大きいのか疑問に思いました。平均mが与えられた場合、偶数の確率は0.5 + e^(-2m)/2と表されることがわかりました。eのべき乗は必ず正の値となるため、回転回数が偶数となる確率も正となります。

この式の証明はここで見ることができます。

x について解きます:

9 x + 12 x = 16 x

匿名

=(log(1+SQRT(5))-log(2))/(log(4)-log(3)) =~ 1.67272093446233.

これが私の解決策です（PDF）。

この問題は、Wizard of Oddsの私のフォーラムで質問され、議論されました。

この問題は、ビデオ「A Difficult Exponential Question」からヒントを得ました。

100人の従業員がいるオフィスで、シークレットサンタのプレゼント交換をします。全員の名前を紙に書き、全員を帽子の中に入れて、ランダムに名前を引いてプレゼントを贈ります。

問題は、平均して閉じたループがいくつあるかということです。

サイズ 4 のクローズドループの例: Gordon が Don に渡し、Don が Jon に渡し、Jon が Nathan に渡し、Nathan が Gordon に渡す。

自分の名前を描くと、サイズ 1 の閉じたループになります。

匿名

(1/1) + (1/2) + (1/3) + ... + (1/100) =~ 5.187377518.

シークレットサンタパーティーに来る従業員が一人だけいるとします。当然、彼は自分で選ぶので、ループは一つになります。

すると、2人目の従業員が遅れてやって来て、一緒に行きたいと申し出ます。彼女には、今いる2人の従業員のリストが渡されます。彼女が従業員1を選ぶ確率は1/2、彼女自身が選ぶ確率は1/2です。もし彼女が従業員1を選んだ場合、彼女は従業員1のループに押し込まれ、従業員1の分を買って、彼が彼女の分を買ってくれることになります。つまり、1 + 0.5 * 1 = 1.5 となります。

すると3人目の従業員が遅れてやって来て、一緒に来たいと申し出ます。彼女には3人になった従業員のリストが渡されます。彼女が従業員1か2を選ぶ確率は2/3、彼女自身が選ぶ確率は1/3です。もし彼女が従業員1か2を選んだ場合、彼女は彼らのループに押し込まれ、自分が選んだ従業員のために買い物をし、本来その従業員のために買い物をするはずだった人が3人目の従業員のために買い物をすることになります。つまり、1.5 + (1/3) = 11/6となります。

すると4人目の従業員が遅れてやって来て、一緒に行きたいと申し出ます。彼女には4人になった従業員のリストが渡されます。彼女が従業員1から3を選ぶ確率は3/4で、彼女自身が選ぶ確率も1/4です。もし彼女が従業員1から3を選んだ場合、彼女は彼らのループに押し込まれ、自分が選んだ従業員の分を買い、本来その従業員の分を買うはずだった人が4の分を買うことになります。つまり、11/6 + (1/4) = 25/12となります。

これを続けると、最終的な答えは 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5.187377518 になります。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

半径1の半円の中に2つの長方形が重なっているとします。2つの長方形の合計面積の最大値はいくらでしょうか？

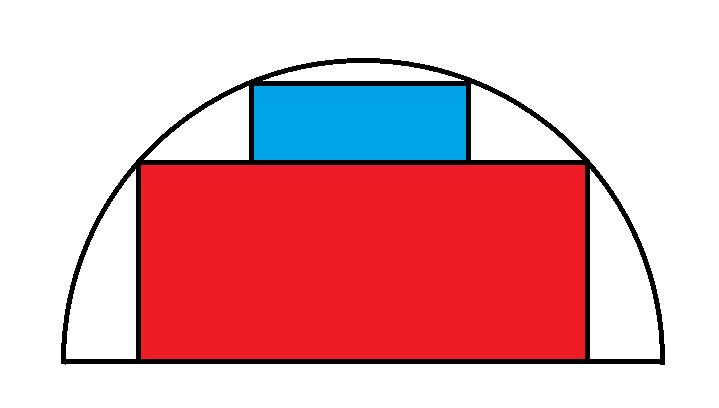
半円の中に2つの長方形

匿名

sqrt(5)-1 =~ 1.236067977499790.

ここに私の完全な解決策（PDF）があります。

この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

一卵性双生児は無視し、すべての子供が男の子か女の子として生まれる確率は50/50であると仮定してください。2人から5人までの特定の人数の家族からランダムに子供を抽出した場合、男の子または女の子に姉妹がいる確率はどれくらいでしょうか？

匿名

興味深いことに、家族の規模に関係なく、男女とも確率は同じです。

例えば、家族が3人の場合を考えてみましょう。男の子と女の子の順番は、以下の8通りの並べ方が考えられます。

BBB
BBG
BGB
BGG
GBB
GBG
GGB
GGG

上記のリストからランダムに女の子を選ぶと、12人の女の子のうち9人に姉妹がいることがわかります。12人の男の子も同様で、9人に姉妹がいます。つまり、確率は9/12 = 3/4です。

子供の数が n の場合、どの子供にも姉妹がいる確率の一般的な公式は、 1-(1/2) n-1です。

家族内の子供の総数に応じて姉妹がいる確率は次のとおりです。

  • 1:0
  • 2: 1/2
  • 3: 3/4
  • 4: 7/8
  • 5: 15/16
  • 6:31/32

あるいは、男の子と女の子の確率が同じになると考えるのも理にかなっています。兄弟姉妹の性別はあなたの性別とは相関しません。つまり、重要なのは家族の人数であり、あなた自身の性別ではありません。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

サバイバーシーズン37のエピソード4で、4つのパズルピースを正方形と正三角形の両方に並べるチャレンジがありました。このパズルを解くには、ピースの正確な寸法はどれくらいでしょうか？

ハバーダッシャースクエア 服飾雑貨店の三角形

匿名

まず、適切な図を作成し、ラベルを付けましょう。

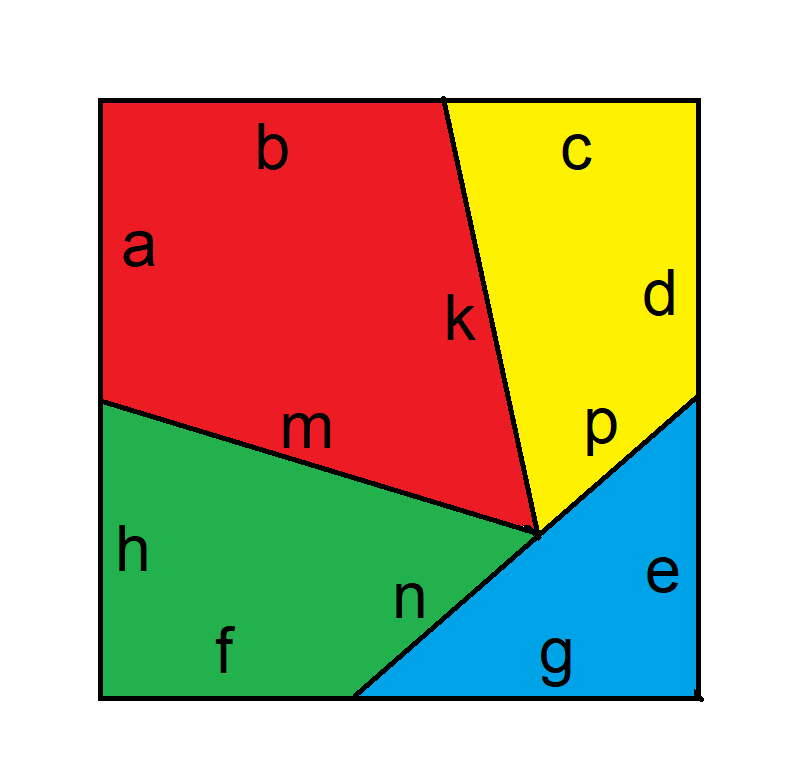
ハバーダッシャーソリューションスクエア

以下は解かれた三角形の図です。

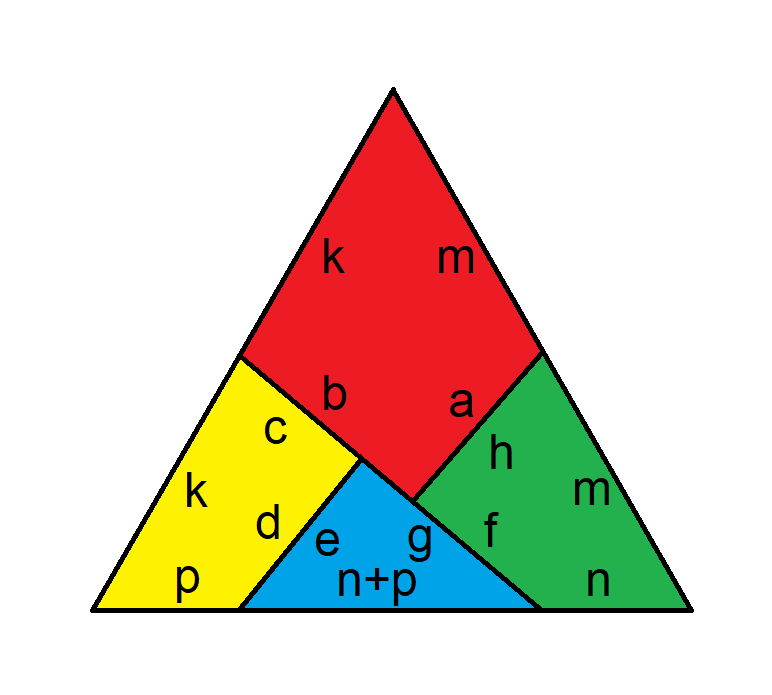
服飾雑貨店のソリューション三角形

次に、正方形の辺の長さが 1 であると仮定して、上の図の各文字の長さを計算します。

[ネタバレ]

a = d = e = h = 1/2

b = g = SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.572145321740575

c = f = 1-SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.427854678259425

k = m = 1/SQRT(SQRT(3)) =~ 0.759835685651592

n = (3-SQRT(4*SQRT(3)-3))/(2*SQRT(SQRT(3))) =~ 0.386767938902275

p = (SQRT(4*SQRT(3)-3)-1)/(2*SQRT(SQRT(3))) =~ 0.373067746749317

[/spoiler]

最後に、私の完全な解決策(PDF) をここに示します。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

きっとあなたは『ビッグバン★セオリー』のファンでしょう。私のお気に入りのシーンの一つは、トカゲとスポックのじゃんけんです。5つのシンボルを使ったじゃんけんのようなもので、ルールは以下のとおりです。

  • 紙は岩を覆う
  • 岩がトカゲを押しつぶす
  • トカゲがスポックに毒を盛る
  • スポックがハサミを叩き壊す
  • はさみは紙を切る
  • トカゲが紙を食べる
    • スポックは岩を蒸発させる
  • はさみがトカゲの首を切る
  • 論文はスポックの反証となる
  • 岩がハサミを粉砕する

私の質問は、ランダムなプレイヤーに対してすべての側が同じチャンスを持つように、さらにシンボルを追加できるかどうかです。

匿名

はい、私もそのシーンが大好きです！ YouTube動画はこちらです。

シンボルの数は奇数である必要があります。理論上は偶数でも構いませんが、その場合、特定のシンボルの組み合わせで引き分けになるようなルールを設けなければなりません。いいえ、両プレイヤーが同じシンボルをプレイした場合にのみ引き分けとなる、決定的なゲームを目指しています。

素数の記号を使うと、特にエレガントで簡単に説明できる解決策があります。例として、7つの記号を使って説明しましょう。次の図のように、記号AからGにラベルを付け、円上に表してみましょう。

rps1

次に、Aから始めて時計回りに次の記号まで矢印を描きます。矢印は、この2つの記号のどちらかに向かいます。まるで、その記号に矢が放たれているかのように考えてください。Aに戻るまで時計回りに描き続けます。図は次のようになります。

rps2

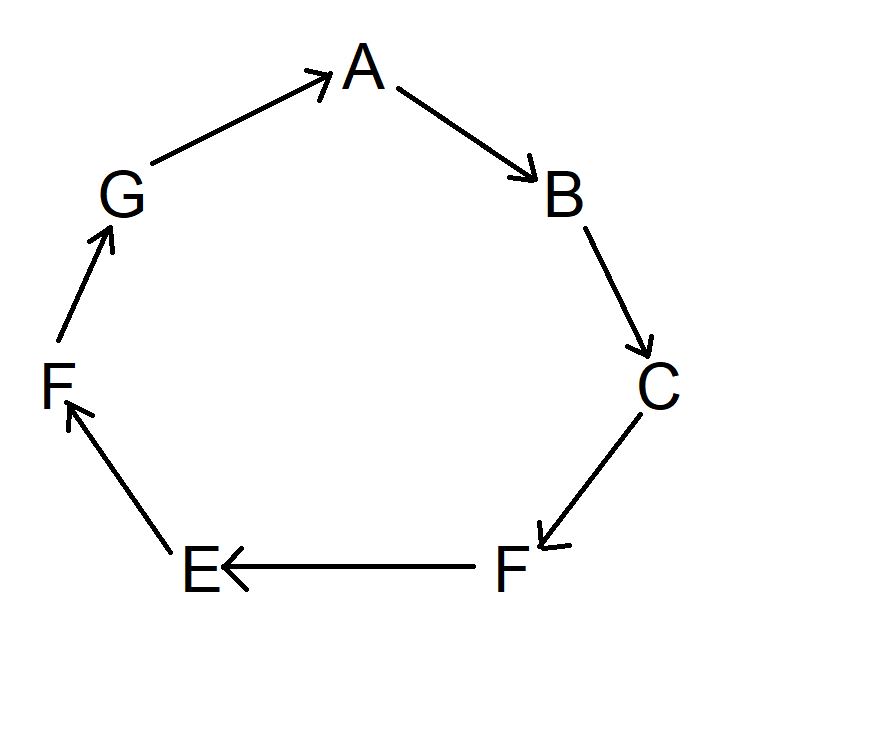
次に、同じことをAから始めて、時計回りに2つずつ記号を進めます。実際には、どこから始めても構いません。図は次のようになります。

rps3

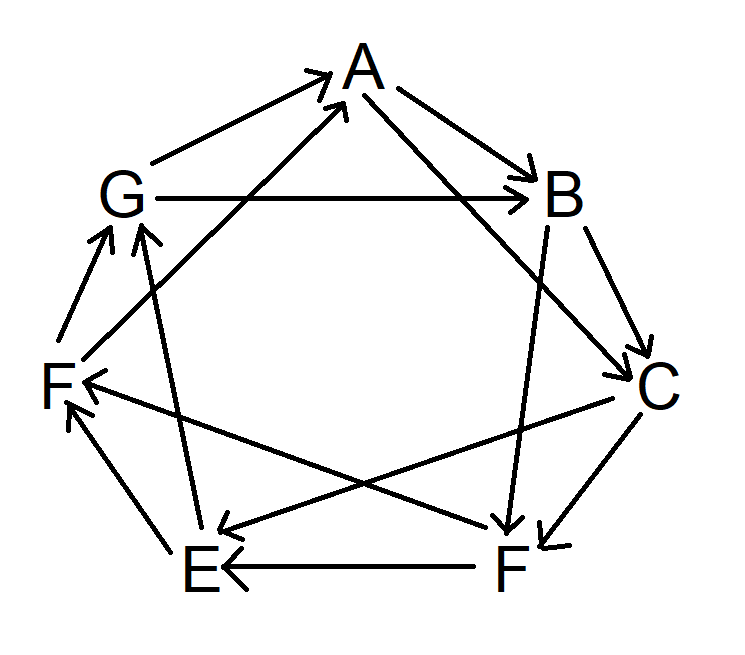
最後に、同じことを時計回りに3つの記号を飛ばして行います。図は次のようになります。

rps4

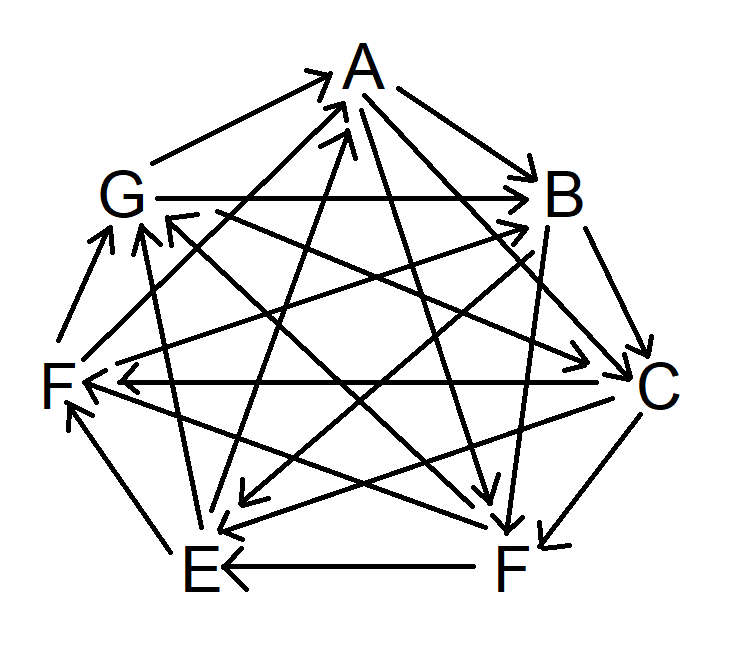
この時点で、すべてのシンボルが他の 3 つのシンボルに勝ち、他の 3 つの異なるシンボルに負けていることに注意してください。

この方法は、元の記号に戻るまでにすべての記号を通過しているため、素数の記号に対しても有効です。n個の記号の場合、このプロセスを(n-1)/2回繰り返す必要があります。

奇数個のシンボルでもバランスの取れたゲームを作ることはできますが、元のシンボルに早く戻ってしまうことがあります。そうなると、見逃したシンボルからもう一度ループを組む必要があります。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

標準的なドミノ（28枚）のセットをシャッフルし、ランダムに1枚引きます。片面を注意深くめくると、6が出てきました。これが6のダブルである確率はどれくらいでしょうか？

Gialmere

ドミノに馴染みのない方のために説明すると、ドミノには2つの面があり、それぞれに0から6の数字が書かれています。セットは、それぞれのドミノが1つずつ含まれます。つまり、7つの数字の中から、無置換で数字を選ぶ組み合わせは、combin(7,2)=21通り、さらに両方の数字が同じ面にある組み合わせは7通りあります。

全 28 個は次のとおりです: 0-0、0-1、0-2、0-3、0-4、0-5、0-6、1-1、1-2、1-3、1-4、1-5、1-6、2-2-2、2-3、2-4、2-5、2-6、3-3、3-4、3-5、3-6、4-4、4-5、4-6、5-5、5-6、6-6。

説明はここまでにして、答えと解決策を述べます。

1/4 = 25%

質問を簡潔に言い換えると、「ランダムに選んだドミノの両面に同じ数字が並ぶ確率は？」となります。答えは単純に7/28 = 1/4です。

答えは1/7だと言うかもしれません。なぜなら、反対側の面は7つの数字のどれかになる可能性があるからです。確かに7つの数字のどれかになる可能性はありますが、すべてが等しく確率的ではありません。6-6のドミノは、6が2つの面にあるため、2回カウントする必要があります。つまり、反対側の面は2つの6のいずれかになる可能性があり、セットには合計8つの6があります。したがって、答えは2/8 = 1/4です。

この質問はWizard of Vegasの私のフォーラムで質問され、議論されています。この質問はAlan Mendelson氏の追悼に捧げられています。

アランとボブは、どちらかが2ゲーム連続で勝つまでテニスをすることにしました。アランがどのゲームでも勝つ確率は2/3です。アランがトーナメントで優勝する確率はどれくらいですか？

匿名

アランとボブは、どちらかが2ゲーム連続で勝つまでテニスをすることにしました。アランがどのゲームでも勝つ確率は2/3です。アランがトーナメントで優勝する確率はどれくらいですか？

答えは16/21 = 76.1905%です。

以下は、アランが個々のゲームに勝つ確率の生成ソリューションです。

p = a が勝つ確率とします。
a を、アランが最後のゲームに勝った後にアランがトーナメントに勝つ確率とします。
b を、ボブが最後のゲームに勝った後にアランがトーナメントに勝つ確率とします。

(1) a = p + (1-p)*b
（2）b = p*a

式(2)を式(1)に代入すると、

a = p + (1-p)*pa
a = p + pa - p 2 *a
a - pa + p 2 *a = p
a(1-p+p 2 ) = p
(3) a = p/(1-p+p 2 )

式(3)を式(2)に代入すると、

b = p 2 /(1-p+p 2 )

最初のゲームでは、トーナメントに勝つ確率が a か b かを決定します。

答え = pa + (1-p)b
= p 2 /(1-p+p 2 ) + (1-p)*p 2 /(1-p+p 2 )
= (2a 2 -a 3 )/(a 2 -a+1)

a=2/3 を代入すると、トーナメントに勝つ確率は 16/21 になります。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。

5フィートのはしごがあります。できるだけ高い壁に立てかけたいと思っています。しかし、1立方フィート×1立方フィートの箱があり、その上にはしごを載せなければなりません。箱を動かすことはできません。はしごの先端は、最大でどのくらいの高さまで届くでしょうか？

匿名

答えは(1 + sqrt(26) - sqrt(23-2*sqrt(26)))/2 =~約4.838501フィートです。

これが私の解決策です（PDF）。

x 1/x が最大となる値はいくつですか?

匿名

答えは e =~ 2.71828182845905 です。

ここで、e^(1/e)の値は~1.44466786100977です。

これが私の解決策です（PDF）。

1944 年の新聞はこの驚くべき偶然に注目しました。

偶然

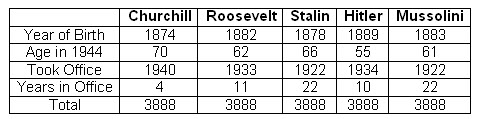
これは大きな偶然でしょうか、それとも何か数学的な仕掛けが関係しているのでしょうか?

Gialmere

これは数学的な仕掛けであり、よく知られているマジックトリックの基礎です。

1944年に生きていた人全員の年齢（誕生日後の年齢）と誕生年を足すと1944年になります。考えてみてください。もしあなたがx歳だったとしたら、1944-x年に生まれたことになります。合計はx + (1944-x) = 1944です。

これは 1944 年の「在職年数」と同じです。在職期間が y 年であれば、1944-y 年に就任したことになります。y + (1944-y) = 1944 です。

1944 + 1944 = 3,888 を合計すると、必ず成立します。

これを 2023 年に機能する魔法のトリックにするには、次の 4 つの合計を対象とする必要があります。

  1. 生年
  2. 今年彼らは何歳になるだろう。
  3. 何らかの重要な出来事が起こった年（最初の子供の誕生など）。
  4. 今年はその重要な出来事の記念日です。

合計は常に 2023 + 2023 = 4046 になります。

この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。