テキサスホールデム - 確率 - 一般
テキサス ホールデム ゲームで 10 人のプレイヤーが 50 ハンドプレイする場合、同じプレイヤーに 2 つのフォーオブアカインドとストレートフラッシュが配られる確率はどれくらいでしょうか。
7枚のカードでフォー・オブ・ア・カインドが揃う確率は0.00168067、ストレートフラッシュが揃う確率は0.00027851です。xをフォー・オブ・ア・カインド、yをストレートフラッシュの確率とすると、求める確率はcombin(50,2)*48*x 2 *y*(1-xy) 47となります。答えは0.0000421845、つまり23,705分の1です。
テキサスホールデムでフラッシュが出る統計的な確率はどれくらいですか?プレイヤーとして、セブンカードスタッドとホールデムのどちらの方がフラッシュが出やすいですか?
テキサス ホールデムのリバーでロイヤル フラッシュが完成する確率はどれくらいですか?
ご存知ない読者のために説明すると、リバーはテキサスホールデムにおける5枚目で最後のコミュニティカードです。プレイヤーは自分の2枚のカードと5枚のコミュニティカードを組み合わせて、最強のポーカーハンドを作らなければなりません。つまり、プレイヤーが7枚のカードでロイヤルフラッシュを形成し、7枚目のカードがロイヤルフラッシュの一部となる確率はどれくらいか、ということです。7枚のカードで5枚のロイヤルフラッシュを形成する確率は、カードを考慮する前で、4*combin(47,2)/combin(52,7) = 4324/133784560、つまり30940分の1です。7枚目のカードがロイヤルフラッシュの一部となる確率は5/7です。つまり、最終的な確率は21620/936491920、つまり43316分の1となります。
テキサス ホールデムでは、フロップから 5 番ストリートまでにインサイド ストレート内に 1 ギャップまたは 2 ギャップを作る確率はどれくらいですか?
読者の皆様のために、この質問は、デッキに47枚残っている場合、ストレート内の1つまたは2つの隙間を2枚のカードで埋める確率を尋ねています。隙間が1つの場合、確率は1-combin(43,2)/combin(47,2) = 0.164662です。隙間が2つの場合、確率は4 2 /combin(47,2) = 0.0148です。
テキサス ホールデムで、フロップ カードがすべて同じスーツの場合、特定のプレイヤーが同じスーツのカードを 2 枚以上持っている確率はどれくらいですか。
同じスートのカードは残り10枚、デッキには49枚残っています。したがって、確率はcombin(9,2)/combin(49,2) = 36/1176 = 0.0306となります。
テキサスホールデムとセブンカードスタッドの様々なハンドの確率は同じですか?それともコミュニティカードによって何か違うのでしょうか?その理由を説明していただけますか?
はい、確率は同じです。52枚のカードのうちランダムに選ばれた7枚のカードは、デッキからどのように取り出されたか、誰と共有したかに関係なく、同じ確率になります。
最初の 2 枚のカードで、ホールデムで 35 ハンド中 7 ハンドでエース キング以上を受け取る確率はどれくらいですか?
エース/キングが出る確率は(8/52)*(4/51) = 0.012066です。ペアが出る確率は(3/51) = 0.058824です。つまり、ペア以上の確率は0.07089です。エース/キング以上の手札が7つ出る確率は、combin(35,7)*(.07089)^7*(1-.07089)^28 = 0.00772です。7以上の確率を計算するには、7から35までを1つずつ計算する必要があります。合計は0.010366551です。
ホールデムのフロップで、ホールカードがすべて同じ場合、4 枚のフラッシュ以上が出る確率をどうやって計算しますか。
同じスートのカードがあと2枚出る確率は、39*combin(11,2)/combin(50,3) = 0.109439です。同じスートのカードがあと3枚出る確率は、combin(11,3)/combin(50,3) = 0.008418です。つまり、同じスートのカードが少なくともあと2枚出る確率は0.117857です。
ウィザードさん、まず最初に、素晴らしいサイトをお持ちですね!しばらく前から拝見しています。ポーカーの質問もチェックしましたが、この質問は見つかりませんでした。別のサイトでは、「テキサスホールデムでは、プリフロップでAKが配られ、リバーでAかKがヒットする確率は2分の1(イーブン)です」と謳っています。直感的に、これはあまりにも高すぎるように思えます。どう思われますか?改めてお礼申し上げます。
親切なお言葉、ありがとうございます。ホールデムに馴染みのない方のために説明すると、これはプレイヤーにエースとキング、そして残りの50枚のカードからランダムに5枚が配られた場合、キングとエース、あるいはその両方がペアになる確率はどれくらいか、という質問に似ています。残りの50枚のうち、44枚はキングでもエースでもありません。44枚の中から任意の5枚を引く方法は、combin(44,5) = 1,086,088通りです。全50枚の中から任意の5枚を引く方法は、combin(50,5) = 2,118,760通りです。つまり、エースとキング、あるいはその両方がペアにならない確率は、1086088/2118760 = 51.26%です。つまり、ペアになる確率は1-51.26% = 48.74%となり、これは2分の1にほぼ等しいです。
テキサス ホールデムで 2 人のプレイヤーが異なるフォーカードを持っている確率はどれくらいですか?
2人のプレイヤーは合計9枚のカードを持ちます。これらのカードは、4枚揃いのカードが2枚と、1枚のシングルトンカードでなければなりません。この組み合わせの数は、combin(13,2)*44 = 3432です。52枚の中から9枚のカードを選ぶ方法の総数は、combin(52,9) = 3,679,075,400通りです。つまり、必ずしも正しい順番ではないものの、正しいカードを持っている確率は、3432/3,679,075,400 = 1,071,992分の1となります。
しかし、カードがAAAABBBBCだからといって、両プレイヤーが異なるフォー・オブ・ア・カインドを持っているとは限りません。5枚のカード1枚と2枚のカード2枚の組み合わせは、9!/(5!*2!*2!) = 756通りあります。9枚のカードの組み合わせは以下の通りです。
フォー・オブ・ア・カインド・バッドビートの組み合わせ
プレイヤー1 | プレイヤー2 | 失敗 | ミラーパターン | パターンごとの組み合わせ | 合計組み合わせ |
AA | BB | AABBC | 2 | 72 | |
AA | AB | ABBBC | 4 | 48 | 192 |
AA | AA | BBBBC | 2 | 6 | 12 |
AA | 交流 | アッーーーーー | 4 | 12 | 48 |
AA | 紀元前 | AABBB | 4 | 24 | 96 |
AB | AB | AABBC | 1 | 144 | 144 |
AB | 交流 | AABBB | 4 | 48 | 192 |
これらのうち、両プレイヤーが異なるフォー・オブ・ア・カインドを持つのは、最初のグループと5番目のグループのみです。つまり、AAAABBBBCのセットから2つの異なるフォー・オブ・ア・カインドが生まれる確率は、168/756 = 22.22%です。
したがって、質問の答えは(3432/3,679,075,400)*(168/756) = 4,823,963分の1です。より現実的な視点で言えば、Party Pokerでは、8の数字が4枚の負けハンドにバッドビート・ジャックポットが付与されます。フォー・オブ・ア・カインドが2枚ある場合、両方が8以上の数字である確率は、combin(7,2)/combin(13,2) = 21/78 = 26.92%です。つまり、2人のプレイヤーが1つのハンドでこのバッドビート・ジャックポットを獲得する確率は、17,917,577分の1です。
昨夜、テキサスホールデムでサイドベットを勧められたのですが、フロップで少なくとも1枚の絵札(または3桁の数字)が出ると言い、賭け金はイーブンマネーだと言われたのですが、この賭けを受け入れるべきだったのでしょうか?
40枚の絵札以外のカードから3枚を選ぶ方法は(40*39*38)/(1*2*3) = 9880通りです。52枚の絵札の中から3枚を選ぶ方法は(52*51*50)/(1*2*3) = 22100通りです。つまり、絵札が出ない確率は9880/22100 = 44.71%です。つまり、絵札が出る確率は55.29%です。つまり、彼の賭けは10.58%の有利な状況でした。
標準的な52枚のカードデッキを使って10人でテキサスホールデムをプレイする場合、各プレイヤーに最初の2枚のカードが配られた後、「フロップ」(次の3枚のカード)がすべて同じスーツになる確率はどれくらいでしょうか?手札のカードがすべて同じスーツ、あるいはそれぞれ異なるスーツの場合、何か違いはありますか?
自分のカードを考慮する前の確率は、4× combin (13,3)/combin(52,3) = 5.1764706%です。
別の見方をすると、フロップの2枚目のカードが同じスーツの1枚目のカードと一致する確率は(12/51)です。フロップの3枚目のカードが同じスーツの1枚目のカードと一致する確率は(11/50)です。(12/51)×(11/50)=5.1764706%。
自分のカードを考慮すると、オッズは多少変わります。同じスートのカードを2枚持っている場合、フロップの確率はpr(同じスートのフラッシュ) + pr(異なるスートのフラッシュ) = combin(11,3)/combin(50,3) + 3×combin(13,3)/combin(50,3) = 5.2193878%となります。
異なるスーツのカードが 2 枚ある場合、スーツが同じフロップになる確率は、pr(同じスーツのフラッシュが共通) + pr(異なるスーツのフラッシュ) = 2×combin(12,3)/combin(50,3) + 2×combin(13,3)/combin(50,3) = 5.1632653% になります。
ウィズさん、あなたの頭脳があればいいのに。いずれにせよ、統計との格闘は続きます。フロップ、ターン、リバー(テキサスホールデム)でフラッシュが完成する確率と、ホールカードのスーツの有無をクロスさせる計算式を考えています。C(50,2) / C(47,5) を試してみましたが、リバーでスーツの揃ったペアの場合はうまくいきませんでした…学校でもっと勉強しておけばよかった!ありがとう!あなたの一番のファンです
優しいお言葉ありがとうございます。でも、私はそんなに頭が良くないんです。数年前にメンサの入会試験を受けたのですが、上位2%に入る条件を満たせませんでした。成績を教えてくれなかったことが今でも悔しいです。1月13日にラスベガスでジェパディのオーディションがあるんですが、予約してあるんですが、それもきっと失敗しちゃうと思います。さて、あなたの質問にお答えします。
スーツのホールカードの場合:
フロップ後のフラッシュ: combin (11,3)/combin(50,3) = 165/19600 = 0.842%。
ターン後のフラッシュ: (combin(11,2)*39/combin(50,3))*(9/47) = 2.096%。
リバー後のフラッシュ: (combin(11,2)*combin(39,2)/combin(50,4))*(9/46) = 3.462%。
スートのないホールカードの場合:
フロップ後のフラッシュ: 0%
ターン後のフラッシュ: 2*combin(12,4)/combin(50,4) = 0.430%。
リバー後のフラッシュ: (2*combin(12,3)*39/combin(50,4))*(9/46) = 1.458%。
ここに累積確率があります。
スーツのホールカードの場合:
フロップによるフラッシュ: 0.842%。
ターンによるフラッシュ:2.937%。
リバーによるフラッシュ:6.400%。
スートのないホールカードの場合:
フロップによるフラッシュ:0.000%
順番にフラッシュする: 0.430%。
リバーによるフラッシュ:1.888%。
ウィザードさん、こんにちは。まず最初に、あなたの的確で無駄のない回答に感心しています。ところで、ホールデムでポケットカードがAAでフロップがKQ9の場合、フルハウスが完成する確率はどれくらいでしょうか? この問題に長年取り組んできましたが、いまだに納得のいく答えが見つかっていません。
エースとK、Q、または9でフルハウスを完成させることができます。残りはエースが2枚、K、Q、9がそれぞれ3枚ずつです。したがって、このような組み合わせは2*3*3=18通りあります。他に考えられるのは、K、Q、または9のペアです。このような組み合わせは3*combin(3,2)=9通りあります。すべての組み合わせの数は47*46/2 = 1081通りです。したがって、確率は(18+9)/1081 = 2.50%です。
長年(あなたがポーカーやスポーツベッティングに興味を持つ前から)大ファンで、「Ask The Wizard」のコラムを毎回楽しみにしていました。また連載を始めてくれて嬉しいです!質問なのですが、近所のカードルームで、特定の時間帯に「Aces Cracked, Win A Rack(エース・クラックド、ウィン・ア・ラック)」というキャンペーンを実施しています。これは、3-6または4-8のテキサスホールデムゲームでポケットエースを持っていてポットに負けた場合、カジノ側がチップラック(100ドル)をくれるというものです。私は、a)ポケットエースがどれくらいの頻度で出るか、b)本来のアグレッシブなプレイで負ける確率はどれくらいか、c)ポットが100ドルなら大抵の場合、負ける確率よりはましなので、最後までチェックして負けるのを待つ方が得策ではないか、といったことを知りたいです。もし統計データをお持ちでしたら、教えていただけると大変助かります!改めて感謝申し上げます。これからも、大勢のプレイヤーを啓蒙し続けてください!
温かいお言葉ありがとうございます。1ハンドでポケットエースが出る確率は6/1326、つまり221ハンドに1回です。私の10人用テキサスホールデムセクション(/games/texas-hold-em/10players.html)によると、ポケットエースで勝つ確率は、プレイヤー全員が最後までプレイを続けると仮定した場合、31.36%です。ただし、これは大きな仮定です。もし強いて推測するなら、実際の10人ゲームでエースで勝つ確率は約70%でしょう。つまり、ポケットエースを出して負ける確率は0.3*(1/221) = 0.1357%です。つまり、1件あたり100ドルとすると、1ハンドあたり13.57セントの価値があります。10人以上でプレイすると、ポーカールームは平均で1ハンドあたり1.36ドルの損失となり、レーキをかなり減らすことになります。私はコールするというあなたの戦略に賛成する傾向にあります。コールすると、より多くのプレイヤーがハンドに残り、負ける可能性が高くなります。
まず初めに、素晴らしいサイトを運営していただき、ありがとうございます。さて、質問です。テキサスホールデムをプレイしていて、フロップで2枚のスモールカードでフラッシュドローが出ました。フラッシュが完成する確率は誰もが知っていますが、本当に知りたいのはハンドを勝ち取る確率です。そして、誰かがそのスートのカードで自分よりも強いカードを持っていると確信しているとします。そこで質問なのですが、そのスートのカードが2枚ではなく1枚だけ出る確率はどれくらいでしょうか?よろしくお願いします。
どういたしまして。つまり、フロップ後のボードに2枚のカードがあり、4枚のフラッシュを持っているということですね。必要なスーツのカードが1枚だけ揃う確率は、9*38/ combin (47,2) = 342/1081 = 31.64%です。
テキサスホールデムで、リバーに同じスーツのコミュニティカードが3枚だけある場合、他のプレイヤーに同じスーツのカードが2枚配られて、私よりも高いフラッシュが完成する確率を知りたいです。例えば、私がスペードの89を持っていて、コミュニティカードにスペードの3、7、Kが含まれている場合、デッキには私の9よりも大きいスペードが4枚あります(TJQA)。誰かに、少なくとも1枚の大きいスペードを含む2枚のスペードが配られる確率はどれくらいでしょうか(9ハンドゲームを想定)。私の最大のホールカードよりも大きいスペードが2枚(または3枚、あるいはx枚)しかない場合はどうでしょうか?ご協力と素晴らしいサイトに感謝いたします。
以下の表は、上位ランクが1~8人、プレイヤーが2~10人(あなた自身を含む)の場合の確率を示しています。あなたの例のように上位ランクが4人、プレイヤーが合計9人の場合、確率は16.45%です。これらの確率の計算方法は、ハンド間の独立性を前提としていますが、これは正確な仮定ではありませんが、結果は概算値に近いものになるはずです。
より高いフラッシュの確率上位ランク(縦)プレイヤー総数(横)ウィザード推定
| 上位ランク | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.71% | 1.41% | 2.11% | 2.80% | 3.49% | 4.17% | 4.85% | 5.52% | 6.19% |
| 2 | 1.31% | 2.61% | 3.89% | 5.15% | 6.40% | 7.62% | 8.84% | 10.03% | 11.22% |
| 3 | 1.82% | 3.60% | 5.36% | 7.08% | 8.77% | 10.43% | 12.05% | 13.65% | 15.22% |
| 4 | 2.22% | 4.40% | 6.52% | 8.60% | 10.63% | 12.61% | 14.56% | 16.45% | 18.31% |
| 5 | 2.53% | 4.99% | 7.39% | 9.72% | 12.00% | 14.23% | 16.39% | 18.50% | 20.56% |
| 6 | 2.73% | 5.38% | 7.96% | 10.47% | 12.91% | 15.29% | 17.60% | 19.85% | 22.03% |
| 7 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
| 8 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
より高いフラッシュの確率上位ランク(下)と総プレイヤー数(横)Mipletシミュレーション
| 上位ランク | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.69% | 1.41% | 2.12% | 2.83% | 3.54% | 4.25% | 4.96% | 5.66% | 6.36% |
| 2 | 1.28% | 2.60% | 3.91% | 5.21% | 6.48% | 7.77% | 9.05% | 10.31% | 11.56% |
| 3 | 1.79% | 3.61% | 5.41% | 7.19% | 8.92% | 10.68% | 12.41% | 14.11% | 15.79% |
| 4 | 2.19% | 4.40% | 6.58% | 8.75% | 10.85% | 12.94% | 15.01% | 17.04% | 19.04% |
| 5 | 2.50% | 5.00% | 7.47% | 9.92% | 12.28% | 14.63% | 16.94% | 19.21% | 21.43% |
| 6 | 2.71% | 5.40% | 8.06% | 10.69% | 13.23% | 15.74% | 18.23% | 20.65% | 23.03% |
| 7 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
| 8 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
素晴らしいサイトですね。個人的な知識として質問させてください。テキサスホールデムを4人でプレイしていました。ポケットエースが配られ、リバーでロイヤルフラッシュが完成しました。エースからスタートした場合、リバーでロイヤルフラッシュが完成する確率はどれくらいでしょうか?
ありがとうございます。ロイヤルが2枚のエースのうち1枚だと仮定すると、リバーまでにロイヤルになる方法は2*46=92通りあります。これはポケットエースの2つのスーツと、もう1枚のカードの46通りの組み合わせになります。50枚のうち5枚が配られる組み合わせは(50,5)=2,118,760通りあります。つまり、確率は92/2,118,760=23,030分の1です。
フロップで同じスーツが 3 枚出てきて、自分がフロップに一致するスーツを持っていない場合、テーブルに 10 人のプレイヤーが残っているとき、誰かがフラッシュを持っている確率はどれくらいですか。
いずれかのプレイヤーがフラッシュを持っている確率は、 combin (11,2)/combin(49,2) = 55/1176 = 4.68%です。ハンド間の独立性を仮定すると(実際にはそうではありません)、9人のプレイヤーがフラッシュを持っていない確率は(1 − 0.0468%) 9 = 64.98%です。つまり、少なくとも1人のプレイヤーがフラッシュを持っている確率は、1-0.6498 = 35.02%です。これはあくまでも簡単な推定値です。ランダムシミュレーションを行った場合、ハンド間の独立性のため、この確率はもう少し高くなると思います。
ウィザード様、最近テキサスホールデムで、スーツが揃った2枚のホールカードが配られた場合にフラッシュが完成する確率を計算しようとしています。私の答えは常に5.8%と出ますが、どうやらこれは間違っているようです。ご協力いただけると大変助かります。
手札と同じスートのカードが3枚揃ってフラッシュが完成する確率は、 combin (11,3)×combin(39,2)/combin(50,5) = 122265/2598960 = 0.057706です。手札と同じスートのカードが4枚揃ってフラッシュが完成する確率は、combin(11,4)×combin(39,1)/combin(50,5) = 2145/2118760 = 0.001012です。手札と同じスートのカードが5枚揃ってフラッシュが完成する確率は、combin(11,5)/combin(50,5) = 462/2118760 = 0.000218です。ボード上で別のスーツでフラッシュが完成する確率は、3×combin(13,5)/combin(50,5) = 3861/2118760 = 0.001822です。これを全て足すと、0.057706 + 0.001012 + 0.000218 + 0.001822 = 0.060759となります。
テキサスホールデムで「ブレイクボード」が発生する確率はどれくらいでしょうか? つまり、ボード上に5枚のカードがあり、ペアが存在せず、フラッシュもストレートも成立しない状態です。
盤上の5つの異なるランクの組み合わせの数は、 combin (13,5)*4 5 = 1287 × 1024 = 1,317,888です。
これらの5つのランクが3つのスーツ(2つのうち2つ、1つのうち1つ)を表す確率は、combin(4,2)*2*combin(5,2)*combin(3,2)=360です。combin(4,2)は、2回表されるスーツについて、4つのスーツから2つを選ぶ方法の数です。2は、1回表されるスーツを選択する2つの方法の数です。Combin(5,2)は、最初の2枚のカードのスーツについて、5つのランクから2つを選ぶ方法の数です。4は、もう1つの2枚のカードのスーツについて、残りの3つのランクから2つを選ぶ方法の数です。
これらの 5 つのランクが 4 つのスーツ、2 つのスーツのうち 1 つ、および 1 つのスーツのうち 3 つを表す確率は、4*combin(5,2)*3*2=240 です。4 は、2 回表されるスーツに対して 4 つのうち 1 つのスーツを選択する方法の数です。Combin(5,2) は、2 つのカードのスーツに対して 5 つのうち 2 つのランクを選択する方法の数です。3 は、1 つの最初のスーツに対して、残りの 3 つのうち 1 つのランクを選択する方法の数です。2 は、1 つの 2 番目のスーツに対して、2 つのうち 1 つのランクを選択する方法の数です。
4 つのスーツを 5 つの異なるランクに配置する方法は 4 5 =1024 通りあります。
したがって、1 つのスートのカードが 2 枚以下になる確率は、(360+240)/1024 = 600/1024 = 58.59% となります。
13段のうち5段を並べる方法は、combin(13,5)=1287通りあります。3段が5段の範囲内に入らない組み合わせは79通りあります。この組み合わせには簡単な公式はありません。すべての組み合わせを繰り返す必要がありました。したがって、段が十分に離れる確率は79/1287 = 6.14%です。
したがって、ボードが壊れる確率は、(1317888/2596960)*(600/1024)*(79/1287) = 1.825211% となります。
ストレートを崩した回数に挑戦されました。79回分のストレートをすべてリストアップしました。
| 2378Q 2378K 2379Q 2379K 237TQ 237TK 237JQ 237JK 237QK 2389K 238TK 238JK 238QK 2479Q 2479K 247TQ 247TK 247JQ 247JK 247QK | 2489K 248TK 248JK 248QK 257TQ 257TK 257JQ 257JK 257QK 258TK 258JK 258QK 267JQ 267JK 267JA 267QK 267QA 267KA 268JK 268JA | 268QK 268QA 268KA 269JA 269QA 269KA 278QK 278QA 278KA 279QA 279KA 289KA 3489K 348TK 348JK 348QK 358TK 358JK 358QK 368JK | 368JA 368QK 368QA 368KA 369JA 369QA 369KA 378QK 378QA 378KA 379QA 379KA 389KA 469JA 469QA 469KA 479QA 479KA 489KA |
シーザーズ・インディアナでテキサスホールデムをプレイしています。シーザーズにはバッドビート・ジャックポットがあり、4枚以上のカードが負けた場合に適用される仕組みです。両プレイヤーはホールカードを2枚ともプレイしなければならず、4人にカードが配られる必要があります。質問なのですが、全員が最後までプレイすると仮定した場合、どのハンドもバッドビートになる確率はどれくらいでしょうか?
私の新しいBad Beat Jackpot セクションでは、10 人のプレイヤーによるゲームでこの種のバッド ビートが発生する確率が 0.0000108、つまり約 93,000 分の 1 であることが示されています。
私の2 人用テキサス ホールデムの確率によると、スーツが K/2 の場合、次のような結果が考えられます。
勝率 51.24%
44.82%の損失
3.94%の引き分け
私のアルティメット・テキサス・ホールデムのテーブルを見ると、プレイヤーはプレイベットでは有利ですが、アンティとブラインドベットでは不利な状況です。この場合、プレイヤーはアンティとブラインドのオッズが悪くなっています。しかし、プレイのオッズは有利です。つまり、最大限にレイズすることで、50%を超える勝率から最大限のバリューを得ているのです。他の2つのベットのオッズが悪いため、全体のバリューは50%を下回っています。レイズ額が少なければ、このバリューはさらに小さくなります。
2008年のワールドシリーズ・オブ・ポーカーで、馬渕元幸選手のクワッドエースがジャスティン・フィリップ選手のロイヤルフラッシュに負けました。この確率について疑問があります。ESPNなどは、約27億分の1と発表していました。彼らは公表されているクワッドエースの発生確率にロイヤルフラッシュの確率を掛け合わせただけのように思えます。この計算方法は正しいのでしょうか?
27億分の1という数字にも同意できません。おっしゃる通り、両プレイヤーがホールカードの両方を使う場合のみ、各プレイヤーの確率を個別に計算し、それを掛け合わせたようです。この方法で計算すると、確率は0.000000000341101、つまり約29億分の1になります。おそらく27億分の1という数字には、両プレイヤーの確率の四捨五入による誤差も含まれているのでしょう。また、確率を2倍にするのを忘れたようですが、その理由は後ほど説明します。
4 つのエースがロイヤル フラッシュに負ける場合、次の 3 つの方法があります。
ケース 1: 一方のプレイヤーはロイヤル フラッシュを 2 枚持っており、もう一方のプレイヤーはエースを 2 枚持っており、ボードには残りの 2 枚のエース、ロイヤルの残りの 2 枚のカード、およびその他のカードが含まれています。
例:
プレイヤー1:

プレイヤー2:

ボード: 




ほとんどのポーカールームでは、バッドビート・ジャックポットを獲得するには、勝者と敗者の両方のプレイヤーがホールカードを2枚ずつ使用する必要があります。これは動画で紹介されているバッドビートの種類で、実際に使われたカードはまさにこれでした。
ケース 2: 一方のプレイヤーはロイヤル フラッシュ (TK) の 2 枚を持っており、もう一方のプレイヤーはエース 1 枚と「空白」のカード 1 枚を持っており、ボードには残りの 3 枚のエースとロイヤルの残りの 2 枚のカードが含まれています。
例:
プレイヤー1:

プレイヤー2:

ボード: 




ケース 3: 一方のプレイヤーはロイヤル フラッシュ (TK) の 1 枚と空白のカードを持っており、もう一方のプレイヤーは 2 枚のエースを持っており、ボードには残りの 2 枚のエースとロイヤル フラッシュの残りの 3 枚のカードが含まれています。
例:
プレイヤー1:

プレイヤー2:

ボード: 




以下の表は、各ケースにおけるプレイヤーとボードの組み合わせの数を示しています。右下のセルには、合計の組み合わせ数が16,896であることを示しています。
バッドビートの組み合わせ
| 場合 | プレイヤー1 | プレイヤー2 | ボード | 製品 |
|---|---|---|---|---|
| 1 | 24 | 3 | 44 | 3,168 |
| 2 | 24 | 132 | 1 | 3,168 |
| 3 | 704 | 3 | 1 | 2,112 |
| 合計 | 8,448 |
しかし、2人のプレイヤーのカードが逆さまになってもバッドビートになる可能性があります。そのため、組み合わせの数を2倍する必要があります。それを調整すると、対象となる組み合わせの合計は2 × 8,448 = 16,896になります。
2人用テキサスホールデムにおける全ての組み合わせの総数は、 combin (52,2) × combin(50,2) × combin(48,5) = 2,781,381,002,400です。つまり、エース4枚がロイヤルフラッシュに負ける確率は、8,448/2,781,381,002,400 = 0.0000000060747、つまり約1億6500万分の1です。ケース1のバッドビートの確率は4億3900万分の1です。動画で報告されているほどオッズが高くない理由は、2つのハンドが重複しており、エースを共有しているからです。つまり、これら2つのイベントは正の相関関係にあります。
「ニューヨークのビデオポーカーの真実を語る」という論文によると、あなたの言う通りです。プレイヤーの結果は確かに運命づけられています。どんなカードを持っていても、運命は避けられません。もしプレイヤーが故意に運命を回避しようとした場合、ゲームは守護天使機能を使ってプレイヤーのミスを修正します。このようなゲームでは、プレイヤーに本物のビデオポーカーをプレイしているのではないこと、そしてペイテーブルはプレイヤーの実際のオッズを示す無意味な指標であることを警告すべきだという著者の意見に、私も完全に同意します。また、こうした偽のビデオポーカーマシンはニューヨークに限ったものではないことも指摘しておきます。
こんにちは。ハワイ出身の中学1年生です。科学フェアでポーカーとシャッフルに関するプロジェクトに取り組んでいます。ポケットテキサスホールデムの勝率をプレイヤー数別に表にしていただき、参考にさせていただいています。プロジェクトを進める上で役立つ質問をいくつか教えていただけないでしょうか。
- グラフに表示されているパーセンテージはどのようにして算出したのですか?
- コンピュータ プログラムを使用した場合、どのように開発し、どのくらいの時間がかかりましたか?
- Wizard of Oddsは趣味で始めたと仰っていましたが、サイトが有名になるにつれて、実験内容は変化しましたか?その理由を教えてください。
- 2人用テーブルは、対戦相手のカード1225枚とコミュニティカード171万2304枚を巡回する総当たりループプログラムによって実行されました。3人から8人の場合、ループ処理に膨大な時間がかかるため、ランダムシミュレーションを行いました。
- 先ほど述べた2つのプログラムを含め、ほぼすべてのプログラムをC++で書いています。残りはJavaかPerlです。ほとんどは他のポーカーベースのプログラムからコピー&ペーストしたものです。新しいコードは1日ほどで書けそうです。
- はい、1997年6月に趣味でサイトを始めました。広告掲載を受け入れ、ビジネスにしようとしたのは2000年1月になってからです。長年にわたり、3つのドメインを経てきました。こちらは1999年5月時点のサイトです。サイトの目的は一貫して、数学に基づいたギャンブル戦略のリソースを提供することです。長年にわたり、ゲームや資料を追加してきました。 2005年シーズンのNFL予想を掲載するという試みもありましたが、これは大失敗でした。
こんにちは、ウィザードさん。テキサスホールデムに関する質問を拝見したのですが、ポケットクイーンを持っている場合、ボードにエースかキングが出る確率は59.85%と計算されているのに気づきました。この数字はどのようにして導き出したのですか?
残りの50枚のカードのうち、5枚のカードの組み合わせは、 combin (50,5)=2,118,760通りあります。そのうち42枚は2-Qです。42枚のうち5枚のカードの組み合わせは、combin(42,5)=850,668通りあります。したがって、キングまたはエースが出ない確率は、850,668/2,118,760 = 40.15%です。したがって、少なくとも1枚のエースまたはキングが出る確率は、1-40.15% = 59.85%です。
別の計算は、1 - pr(フロップの最初のカードがエースまたはキングではない) × pr(フロップの 2 番目のカードがエースまたはキングではない) × pr(フロップの 3 番目のカードがエースまたはキングではない) × pr(フロップの 4 番目のカードがエースまたはキングではない) × pr(フロップの 5 番目のカードがエースまたはキングではない) = 1 - (42/50) × (41/49) × (40/48) × (39/47) × (38/46) = 59.85% です。
テキサス ホールデムで同じスーツのカードが 2 枚ある場合、フロップで同じスーツのカードがあと 2 枚出る確率はどれくらいでしょうか。
同じスートのカードが2枚以上揃う組み合わせは(11,2)=55通り、スートの違うカードが1枚揃う組み合わせは39通りあります。フロップで可能なカードの組み合わせは、合計で(50,3)=19,600通りあります。つまり、フロップ後にフラッシュが4枚揃う確率は、55×39/19,600 = 10.94%です。
私はオンラインポーカーに参加していたのですが、これが起こる確率を知りたいです。
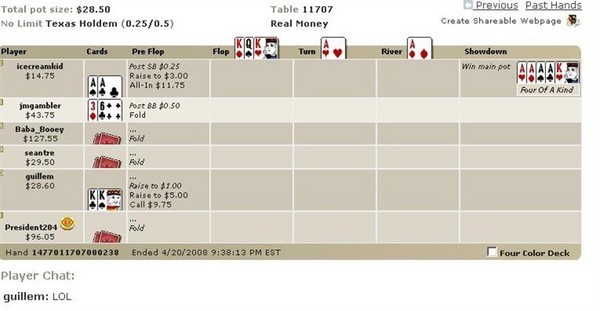
普段はバッドビートの質問にはうんざりしているのですが、これは無視できないほど辛かったです。最初のカードが配られる前に、2人プレイで両プレイヤーがポケットペアを持っている場合、4枚のキングが4枚のエースに負ける確率は、2* combin (4,2)*combin(4,2)*44/(combin(52,2)*combin(50,2)*combin(48,5)) = 2*6*6*44/(1326*1225*1712304) = 877,961,175分の1です。これは6人プレイなので、combin(6,2) = 15通りの異なるペアが存在します。6人プレイでは、この確率は15倍、つまり58,530,745分の1になります。指定されたホールカードが配られた後、フロップの前に、ハンドがこのように終了する確率は 38,916 分の 1 です。
ラスベガスのカードルームでプロモーションを実施しています。4つのスーツ全てでフラッシュを完成させると400ドル獲得できます。ホールカードを2枚とも使用しなければならず、5時間の制限時間があります。1時間あたり35ハンドで、最初のフラッシュからカウントダウンが始まると仮定した場合、5時間以内に残りの3つのフラッシュを完成させる確率はどれくらいでしょうか?ありがとうございます。
最初のフラッシュがスペードだとしましょう。1時間あたり35ハンドだとすると、5時間で175ハンドプレイできます。つまり、ハート、ダイヤ、クラブでフラッシュを作れるハンドは175ハンドあります。プレイヤーは、必要なスーツのいずれかでフラッシュが完成する可能性のあるハンドを決してフォールドしないと仮定します。
特定のスーツ(例えばハート)のフラッシュを両方のホールカードで完成させる確率は、combin(13,2)×[combin(11,3)×combin(39,2) + combin(11,4)×39 + combin(11,5)]/(combin(52,2)×combin(50,5)) = 10576566/2809475760=0.003764605となります。次の175ハンドでハートのフラッシュを逃す確率は(1-0.003764605) 175 =0.51682599となります。
他の3つのスーツが揃わない確率をpr(ハートのフラッシュがない)+pr(ダイヤモンドのスーツがない)+pr(クラブのフラッシュがない)とするのは誤りです。なぜなら、そのうち2つのスーツが揃わない確率を二重に計算することになるからです。したがって、pr(ハートまたはダイヤモンドのフラッシュがない)+pr(ハートまたはクラブのフラッシュがない)+pr(クラブまたはダイヤモンドのフラッシュがない)を足し合わせる必要があります。しかし、そうすると3つのフラッシュ全てが揃わない確率が誤って差し引かれてしまいます。したがって、pr(クラブ、ダイヤモンド、ハートのフラッシュがない)を足し合わせる必要があります。
175 ハンドをプレイして、特定の 2 つのスーツのどちらも手に入らない確率は、(1-2×0.003764605) 175 =0.266442448 です。
175 ハンドをプレイして、残りの 3 つのスーツのいずれも手に入らない確率は、(1-3×0.003764605) 175 =0.137015266 です。
したがって答えは 1-3×0.51682599 + 3×0.266442448 - 0.137015266 = 0.111834108 です。
この問題に関してご助力いただいたdwheatleyさんに感謝します。Wizard of Vegasの私の掲示板でも議論されています。
ドイル・ブランソンは、1976年と1977年のワールドシリーズ・オブ・ポーカーのメインイベントで優勝したことで有名です。どちらの場合も彼は10-2のホールカードを持ち、リバーでフルハウスを完成させました。そのオッズはどれくらいでしょうか?
異なるランクのカードが2枚ある場合、フルハウスが完成する確率は121.6分の1です。リバーでフルハウスが完成する確率は207分の1です。
リバーで 2 回のうち 2 回このようなハンドが完成する確率は 43,006 分の 1 です。
ランクのみで同じ 2 枚の開始カードでこれが発生する確率は、3,564,161 分の 1 です。
両方の場合ともちょうど 10-2 でこれが起こる確率は、295,379,826 分の 1 です。
VFWのポーカーナイトから帰ってきたところです。6-6のホールが3回連続で出ました!こんなことは初めてです。一晩で同じランクのポケットペアが3回連続で出る確率はどれくらいでしょうか? 一晩で合計120ラウンドあると仮定してもいいでしょう。
答えと解決方法は以下のネタバレタグに記載されています。
[ネタバレ]特定の時点では、次の 4 つの状態が考えられます。
- 状態 1: 最初のハンド、または最後のハンドがポケット ペアではなかったハンド。
- 状態 2: 最後のハンドはポケット ペアでした。
- 状態 3: 最後の 2 つのハンドは同じポケット ペアでした。
- 状態 4: 同じポケット ペアが 3 つ連続してすでに達成されています。
状態1にいる場合、3/51の確率で状態2に進むことができます。それ以外の場合は、状態1に留まります。
状態2の場合、(4/52)×(3/51)の確率で状態3に進むことができます。それ以外の場合は、状態1に戻ります。
状態3の場合、(4/52)×(3/51)の確率で状態4に進むことができます。それ以外の場合は、状態1に戻ります。
状態 4 の場合は、そのままの状態を維持します。
つまり、遷移行列 T は次のように作成できます。
| 0.941176 | 0.058824 | 0.000000 | 0.000000 |
| 0.941176 | 0.054299 | 0.004525 | 0.000000 |
| 0.941176 | 0.054299 | 0.000000 | 0.004525 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
合計 120 回のハンドがプレイされるので、T^120 を求めます。
| 0.941044 | 0.058549 | 0.000265 | 0.000141 |
| 0.941025 | 0.058548 | 0.000265 | 0.000162 |
| 0.936786 | 0.058284 | 0.000264 | 0.004666 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
右上のセルには、3 ハンド シーケンスで状態 1 から開始して 120 回のスタート ハンド後に状態 4 に至る確率 (0.000141471) が表示されます。
その数の逆数を取ると、確率は 7068.605131 分の 1 になります。
[/spoiler]この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
映画「カジノ・ロワイヤル」のポーカー トーナメントの最終ハンドで、4 人のプレイヤーのハンドは次のようになります。
- フラッシュ
- フルハウス
- フルハウス(最初のものとは異なる価値)
- ストレートフラッシュ
その確率はどれくらいですか?
これについてはシミュレーションをしなければなりませんでした。私のシミュレーションでは、誰も降りないという仮定をしています。約22億ラウンド実行した結果、312回降りました。これは約700万分の1の確率に相当します。


