このページ
ボーナスクラップス
概要
ボーナスクラップスは、クラップスにある3つのサイドベットのセットです。以下の通りです。
- スモール — シューターが 2 から 6 までのすべての合計を出した後、合計 7 を出した場合に勝ちます。勝ちは通常 30 対 1 で支払われます。
- トール — シューターが合計 7 を出す前に、8 から 12 までのすべての合計を出すと勝ちます。勝ちは通常 30 対 1 で支払われます。
- すべて — シューターが 7 以外の 2 から 12 までのすべての合計を出した後、合計が 7 になった場合に勝ち。勝ちは通常 150 対 1 で支払われます。
2021年、私はベネチアンで「ダイセオロジー」と呼ばれる同じ賭けを見始めました。
分析
次の表は、勝利した場合の配当が 30 対 1 の場合のスモール ベットとトール ベットの分析を示しています。右下のセルには、ハウス エッジが 18.30% であることがわかります。
小柄で背が高い
| イベント | 支払う | 確率 | 戻る |
|---|---|---|---|
| 勝つ | 30 | 0.026354 | 0.790617 |
| 損失 | -1 | 0.973646 | -0.973646 |
| 合計 | 1.000000 | -0.183029 |
かつては、スモールとトールの配当が34倍になるテーブルもあったことが知られています。これらのより寛大なオッズには、7.76%のハウスエッジがあります。
次の表は、勝利が 150 対 1 で支払われる場合の All ベットの分析を示しています。右下のセルには、ハウス エッジが 20.61% であることがわかります。
全て
| イベント | 支払う | 確率 | 戻る |
|---|---|---|---|
| 勝つ | 150 | 0.005258 | 0.788655 |
| 損失 | -1 | 0.994742 | -0.994742 |
| 合計 | 1.000000 | -0.206087 |
オールベットでは、155対1や175対1といった配当も見かけました。「フォーワン」オッズから「トゥワン」オッズに変換するには、配当から1を引くことを忘れないでください。以下の表は、150対175の5で割り切れるすべての配当のハウスエッジを示しています。
All Betのハウスエッジ概要
| 支払う | ハウスエッジ |
|---|---|
| 150 | 20.61% |
| 155 | 17.98% |
| 160 | 15.35% |
| 165 | 12.72% |
| 170 | 10.09% |
| 175 | 7.46% |
方法論
私はボーナスクラップスを次の 3 つの方法で分析しました。
- シミュレーション — これはおそらく最も簡単な方法でしょう。しかし、私のような数学純粋主義者にとって、シミュレーションは知的に満足感を与えるものではありません。
- マルコフ連鎖 — この方法は面倒で時間がかかります。SmallとTallの場合は6x6の遷移行列、Allの場合は12x12の遷移行列が必要になります。
- 積分法 — この方法は、積分計算機を使えば驚くほど簡単です。以下で詳しく説明します。
重要な出来事がサイコロを振って一つずつ決まるのではなく、一つの瞬間として捉えると想像してみてください。出来事間の時間は記憶を持たない性質を持ち、出来事間の平均時間は1単位時間であると仮定します。言い換えれば、出来事間の時間は平均が1の指数分布に従います。賭けの判定においては、これは問題になりません。なぜなら、出来事は一つずつしか起こらないからです。
以下は、与えられた合計が x 単位時間内に少なくとも 1 回は出ていない確率です。
- 2または12: exp(-x/36)
- 3または11: exp(-x/18)
- 4または10: exp(-x/12)
- 5または9: exp(-x/9)
- 6または8: exp(-5x/36)
- 7: exp(-x/6)
まずはスモールベットを見てみましょう。トールベットのオッズは全く同じです。
x 単位の時間で、2、3、4、5、6 が出ていて、7 が出ていない確率は次のとおりです: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6) プレイヤーがそれまでに 2 から 6 までのすべての合計を出した後、時刻 x に 7 を出す確率は次のとおりです:
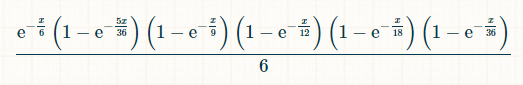
積分にはこの積分計算機を使用しました。
7が出る可能性はいつでもあるので、当選確率は、この確率を0から無限大までxで積分したものになります。知っておく必要はありませんが、積分の極限を適用する前の積分は、 (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^ (-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(- (7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^ (-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6。
積分の限界を適用すると、答えは 20049 / 760760 = 約 0.02635390924864609 になります。
次に、オールベットを見てみましょう。
x 単位の時間で、2、3、4、5、6、8、9、10、11、12 が出ていて、7 が出ていない確率は次のとおりです: (1-exp(-x/36)) 2 *(1-exp(-x/16)) 2 *(1-exp(-x/12)) 2 *(1-exp(-x/9)) 2 *(1-exp(-5x/36)) 2 *exp(-x/6) プレイヤーがそれまでに 2 から 6 までのすべての合計を出した後、時刻 x に 7 を出す確率は次のとおりです:
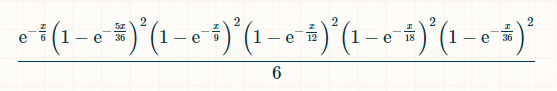
7が出る可能性はいつでもあるため、当選確率は、この確率を0から無限大までxで積分したものになります。必ずしも知る必要はありませんが、積分の極限を適用する前の積分は、(-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1)となります。 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6。
積分の限界を適用すると、答えは 126538525259 / 24067258815600 = 0.0052577040961964420049 になります。



