このページ
異なるダブル
概要
ディファレント・ダブルスは、ビロクシのボー・リヴァージュ・カジノで見られるクラップスのサイドベットです。シューターが合計7が出る前に出したダブルの数に応じて配当が決まります。配当表は以下の通りです。
- 6回のダブルは100対1の配当
- 5回のダブルは15対1の配当
- 4回のダブルは8対1の配当
- 3回のダブルで4対1の配当
分析
下の表は、あらゆる可能性のある結果の確率とリターンへの寄与を示しています。右下のセルにはハウスエッジが27.92%(痛い!)と表示されています。
異なるダブルリターンテーブル
| ダブルス | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| 6 | 100 | 1 | 0.001082 | 0.108225 |
| 5 | 15 | 6 | 0.006494 | 0.097403 |
| 4 | 8 | 21 | 0.022727 | 0.181818 |
| 3 | 4 | 56 | 0.060606 | 0.242424 |
| 2 | -1 | 126 | 0.136364 | -0.136364 |
| 1 | -1 | 252 | 0.272727 | -0.272727 |
| 0 | -1 | 462 | 0.500000 | -0.500000 |
| 合計 | 924 | 1.000000 | -0.279221 |
代数解析
ダブルが出る確率は1/36です。したがって、ダブルが出る確率は6/36 = 1/6です。セブンが出る確率も1/6です。ダブルとセブン以外の出目は無視できます。したがって、賭けに関連する出目があったと仮定すると、その出目の確率は以下のようになります。
- 任意の倍数 = 1/2
- 7つ = 1/2
最初の有効なロールで7が出る確率は1/2です。したがって、ダブルが出る確率はゼロです。
そうでなければ、プレイヤーはダブルを出したはずです。これで、ダブルをもう一度出すことは重要なイベントとして無視できます。両方の重要なイベントの確率は次のようになります。
- 有意なダブル = 5/11
- 7つ = 6/11
この時点でプレイヤーが7を出してダブルが1回出る確率は6/11です。したがって、ダブルが1回出る確率は(1/2)*(6/11) = 3/11 = 約27.27%となります。
そうでなければ、プレイヤーは2回目のダブルを出していたはずです。これで、2つの異なるダブルが出た場合を重要なイベントとして無視できます。両方の重要なイベントの確率は次のようになります。
- 有意なダブル = 4/10
- 7つ = 6/10
この時点でプレイヤーが7(ダブルが2回出る)を出す確率は6/10です。したがって、ダブルが1回出る確率は(1/2)*(5/11)*(6/10) = 3/22 = 約13.6363636%となります。
そうでなければ、プレイヤーは3回目のダブルを出していたはずです。これで、3つの異なるダブルが出ることは重要なイベントとして無視できます。両方の重要なイベントの確率は次のようになります。
- 有意なダブル = 3/9
- 7つ = 6/9
この時点でプレイヤーが7(ダブルが2回出る)を出す確率は6/9です。したがって、ダブルが1回出る確率は(1/2)*(5/11)*(4/10)*(6/9) = 2/33 = 約6.060606%となります。
そうでなければ、プレイヤーは4回目のダブルを出していたはずです。これで、4つの異なるダブルが出ることは重要なイベントとして無視できます。両方の重要なイベントの確率は次のようになります。
- 任意の有意な倍数 = 2/8
- 7つ = 6/8
この時点でプレイヤーが7(ダブルが2回出る)を出す確率は6/8です。したがって、ダブルが1回出る確率は(1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = 約2.272727%となります。
そうでなければ、プレイヤーは5回目のダブルを出していたはずです。これで、5回連続でダブルが出ることは重要なイベントとして無視できます。両方のタイプの重要なイベントの確率は次のようになります。
- 有意な2倍の値 = 1/7
- 任意の7 = 6/7
この時点でプレイヤーが7(ダブルが2回出る)を出す確率は6/7です。したがって、ダブルが1回出る確率は(1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = 約0.649351%となります。
そうでなければ、プレイヤーは最後のダブルを出していたはずです。その確率は(1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = 約0.108225%です。
これらすべてを上記の返値表にまとめると、組み合わせの数は924通りになります。
積分解析
重要な出来事がサイコロを振って一つずつ決まるのではなく、一つの瞬間として捉えると想像してみてください。出来事間の時間は記憶を持たない性質を持ち、出来事間の平均時間は1単位時間であると仮定します。言い換えれば、出来事間の時間は平均が1の指数分布に従います。賭けの判定においては、これは問題になりません。なぜなら、出来事は一つずつしか起こらないからです。
特定のダブルイベント間の時間は、平均12の指数分布に従います。12である理由は、重要なイベントが発生した場合、その特定のダブルイベントが1/12の確率で発生するためです。したがって、特定のダブルイベントがx単位時間内に発生しなかった確率はexp(-x/12)です。したがって、特定のダブルイベントが発生した確率は1-exp(-x/12)です。
賭け開始からの経過時間をxとします。すべてのダブルが出てきて、7が出ない確率は(1-exp(-x/12)) 6 ×exp(-x/2)です。
これをxの時点で7が出る確率で締めくくるには、7が出る確率の1/2を掛けて、ちょうどxの時点での当選確率は(1/2)×(1-exp(-x/12)) 6 ×exp(-x/2)となる。
全期間にわたって賭けが勝つ確率を求めるには、1 から無限大まで積分します。
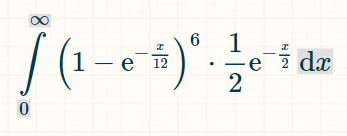
これを積分するには、この積分計算機をおすすめします。積分フィールドに「(1-exp(-x/12))^6*(1/2)*exp(-x/2)」と入力します。積分の限界については、オプションで0と∞を入力します。「実行」をクリックします。「以下の積分が得られます。
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40 *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
ただし、0を入力する必要はありません。計算機は1/924 = 約0.001082251082251082と答えます。
5つの異なる倍精度実数の積分を示します。6と表示されているのは、6つの倍精度実数が存在し、それらが生成されなかったためです。
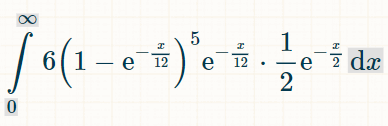
x 単位時間内に勝利する確率は次のとおりです。
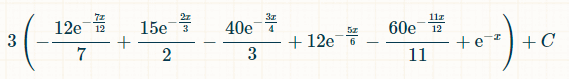
0 から無限大までの積分の境界を置くと、ちょうど 5 つの異なるダブルが出る確率は 1/154 です。
4つの異なる倍精度数の積分です。15個になる理由は、6つの倍精度数のうち4つの組み合わせが6!/(4!*2!) = 15通りあるからです。
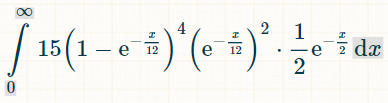
x 単位時間内に勝利する確率は次のとおりです。
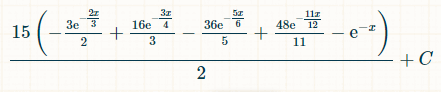
0 から無限大までの積分の境界を置くと、正確に 4 つの異なるダブルが出る確率は 1/44 です。
3つの異なる倍精度実数値の積分です。20とあるのは、6つの倍精度実数値のうち3つの組み合わせが6!/(3!*3!) = 20通りあるためです。
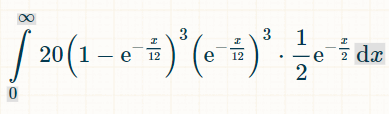
x 単位時間内に勝利する確率は次のとおりです。
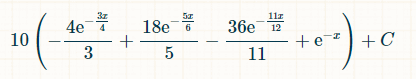
0 から無限大までの積分の境界を置くと、正確に 3 つの異なるダブルが出る確率は 2/33 です。



