このページ
ファイアベット
概要
ファイアーベットはクラップスで人気のサイドベットで、シューターが獲得したユニークポイントの数に応じて配当が決まります。以下の3つの配当表を私は知っています。それぞれのハウスエッジは表の一番下の行に記載されています。最も一般的なのは配当表1です。配当は「1対1」で示され、マイナスは負けを意味します。
ファイアベットのペイテーブル
| 獲得ポイント | ペイテーブルA | ペイテーブルB | ペイテーブルC |
|---|---|---|---|
| 6 | 999 | 2000 | 299 |
| 5 | 249 | 200 | 149 |
| 4 | 24 | 10 | 29 |
| 3 | -1 | -1 | 6 |
| 2 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 |
| 0 | -1 | -1 | -1 |
| ハウスエッジ | 20.76% | 24.86% | 20.73% |
以下はペイテーブル A の私の分析です。右下のセルにはハウスエッジが 20.76% と表示されています。
ファイアベット — ペイテーブルA
| 獲得ポイント | 支払う | 確率 | 戻る |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 24 | 0.008798 | 0.211156 |
| 5 | 249 | 0.001640 | 0.408343 |
| 6 | 999 | 0.000162 | 0.162272 |
| 合計 | 1 | -0.207628 |
以下はペイテーブル B の私の分析です。右下のセルにはハウスエッジが 24.86% と表示されています。
ファイアベット — ペイテーブルB
| 獲得ポイント | 支払う | 確率 | 戻る |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 10 | 0.008798 | 0.087982 |
| 5 | 200 | 0.001640 | 0.327987 |
| 6 | 2000 | 0.000162 | 0.324869 |
| 合計 | 1 | -0.248562 |
以下はペイテーブル C の私の分析です。右下のセルには、ハウス エッジが 20.73% と表示されています。
ファイアベット — ペイテーブルC
| 獲得ポイント | 支払う | 確率 | 戻る |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | 6 | 0.033434 | 0.200605 |
| 4 | 29 | 0.008798 | 0.255147 |
| 5 | 149 | 0.001640 | 0.244350 |
| 6 | 299 | 0.000162 | 0.048568 |
| 合計 | 1 | -0.207295 |
次の表は、Excel が処理できる限りの有効数字を使用して、0 から 6 ポイントになる確率を示しています。
ファイアベットの確率
| 獲得ポイント | 確率 |
|---|---|
| 0 | 0.593939393939394 |
| 1 | 0.260750492003903 |
| 2 | 0.101275355549231 |
| 3 | 0.0334342121788456 |
| 4 | 0.00879817844040312 |
| 5 | 0.00163993313895325 |
| 6 | 0.000162434749269826 |
上記の確率の計算方法をよく聞かれます。これは数学的に難しい問題です。以下に、0から6までの任意の数のポイントを作る確率を求める3つの方法を列挙します。
ランダムシミュレーション
ランダムシミュレーションは、Fire Betを分析する最も簡単な方法です。現代のコンピュータの速度を考えると、非常に正確です。厳密な解を求めるのは、(私のような)数学的純粋主義者だけです。次の表は、ペイテーブルAに基づいて約400億回のFire Betをシミュレーションした結果です。右下のセルはハウスエッジが20.7531%であることを示しています。実際のハウスエッジは20.7628%なので、シミュレーションの精度はリターンの0.01%でした。
ファイアベットシミュレーション
| 獲得ポイント | 支払う | 勝利 | 確率 | 戻る |
|---|---|---|---|---|
| 6 | 999 | 6,452,452 | 0.000162 | 0.162257 |
| 5 | 249 | 65,165,019 | 0.001640 | 0.408438 |
| 4 | 24 | 3億4,955万3,690円 | 0.008799 | 0.211173 |
| 3 | -1 | 1,328,267,592 | 0.033435 | -0.033435 |
| 2 | -1 | 4,023,371,732 | 0.101275 | -0.101275 |
| 1 | -1 | 10,358,742,102 | 0.260747 | -0.260747 |
| 0 | -1 | 23,595,605,529 | 0.593941 | -0.593941 |
| 合計 | 39,727,158,116 | 1.000000 | -0.207531 |
マルコフ連鎖
ファイアベットのオッズを正確に計算する方法の一つは、マルコフ連鎖を使うことです。これは、既に完了したポイントの64通りの状態のいずれかを前提として、将来の任意のポイント数を完了する確率を計算することを意味します。計算は終盤では比較的簡単で、あと1ポイントあれば6つすべて完了します。その後、最初のロールの開始状態まで遡っていきます。
この最初の状態は、列見出しを除いた表の最初の行として表されます。これは、0から6までの任意の数のポイントを完了する上記の確率を示しています。
ファイアベットマルコフ連鎖
| ポイント すでに 作った | 確率 0 ポイント | 確率 1 ポイント | 確率 2ポイント | 確率 3ポイント | 確率 4ポイント | 確率 5ポイント | 確率 6ポイント |
|---|---|---|---|---|---|---|---|
| なし | 0.593939 | 0.260750 | 0.101275 | 0.033434 | 0.008798 | 0.001640 | 0.000162 |
| 10 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 9 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0.022402 | 0.004153 | 0.000404 |
| 9,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 8 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 8,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 8,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 6,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 6,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6,8 | 0.000000 | 0.000000 | 0.732710 | 0.210728 | 0.048135 | 0.007762 | 0.000665 |
| 6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0。022402 | 0.004153 | 0.000404 |
| 5,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 5,9 | 0.000000 | 0.000000 | 0.685315 | 0.237358 | 0.064328 | 0.011875 | 0.001124 |
| 5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 5,8 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.876957 | 0.114977 | 0.008066 |
| 5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.934446 | 0.065554 |
| 4 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 4,10 | 0.000000 | 0.000000 | 0.647934 | 0.250930 | 0.079930 | 0.018752 | 0.002454 |
| 4,9 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,8 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0。188851 | 0.024790 |
| 4,6 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 4,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.816667 | 0.164832 | 0.018502 |
| 4,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,5,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,5,9 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 4,5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.758221 | 0.208531 | 0.033248 |
| 4,5,8 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0。934446 | 0.065554 |
| 4,5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
私の作品を再現しようと考えている方のために、ある状態から別の状態へ移行する際のアドバイスをいくつかご紹介します。まずは、シューターが既に5ポイントを獲得している、終わりに近い状態から始めましょう。例えば、シューターが4だけを獲得する必要がある場合、以下の3つのことが起こります。(1) 4を確立して獲得する、(2) 既に獲得したポイントを確立して獲得する、(3) 7でアウトになる。(1)の確率は(3/24)*(1/3) = 1/24 = 0.041667です。(2)の確率は(4/24)*(2/5) + (5/24)*(5/11) + (5/24)*(5/11) + (4/24)*(2/5) + (3/24)*(1/3) = 0.364394です。 (3) の確率は 1 - 0.041667 - 0.364394 = 0.593939 です。最終的には (1) または (3) のいずれかの事象が発生します。(1) が (3) より先に発生する確率は 0.041667/(0.041667+0.593939) = 0.065554 です。再帰的に開始点まで戻ります。これは時間がかかり、冗長で退屈な作業になりますが、スプレッドシートを使って自動的に行うこともできます。
微積分
この方法の最初のステップは、ポイントが確定した後、パスラインベットの7つの可能な結果すべてについて確率を計算することです。カムアウトロールでプレイヤーがすぐに勝つか負けるかの12通りの組み合わせ、つまり1/3の確率は無視できます。これらのイベントはファイアベットにとって重要ではないためです。したがって、最初のロールは36通りではなく24通りの組み合わせに基づいています。
- 4ポイント獲得と勝利 = (3/24) × (3/9) = 1/24 = 約4.17%
- 獲得した5ポイントと勝利 = (4/24) × (4/10) = 1/15 = 約6.67%
- 6ポイント獲得と勝利 = (5/24) × (5/11) = 25/264 = 約9.47%
- 8ポイント獲得と勝利 = (5/24) × (5/11) = 25/264 = 約9.47%
- 9ポイント獲得と勝利 = (4/24) × (4/10) = 1/15 = 約6.67%
- 獲得した10ポイントと獲得したポイント = (3/24) × (3/9) = 1/24 = 約4.17%
- 得点と7アウト = 2×((3/24) × (6/9))+ 2×((4/24) × (6/10)) + 2×((5/24) × (6/11)) = 98/165 = 約59.39%
これらの確率の合計は 1 になることに注意してください。
次に、ファイアベットが2つのサイコロを1つずつ振って決定されるのではなく、イベント間の時間がランダムに発生し、イベント間の時間が平均1単位時間となる指数分布に従うと仮定します。イベントが発生した場合、そのイベントは先ほど計算したクラップスの確率に従います。
例えば、ポイント4の勝利の確率は1/24です。したがって、ポイント4の勝利間の時間は平均24単位になります。ポイント10の勝利がx単位時間ない確率はexp(-x/24)です。つまり、x単位時間内に少なくとも1回のポイント10の勝利が発生する確率は1-exp(-x/24)です。
ファイアベットの判定において、イベント間の経過時間は関係なく、イベントの内容が重要です。したがって、以下のようにして、賭けの勝者を全期間にわたって積分することができます。
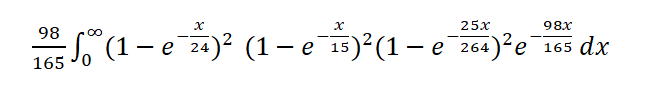
この積分の意味を説明しましょう。これは、x単位時間後に、7以外のすべてのポイントで少なくとも1回の勝利があった確率です。4と10の勝利の確率は同じなので、4の勝利の確率を2乗できます。5と9、6と8についても同様です。最後に、この全体に98/165、つまり7アウトの確率を掛けて賭けを終了します。そうしないと、プレイヤーは重複した勝利に対して報酬を受け取る可能性があります。
これを手作業で積分するのは非常に面倒で、間違いも起こりやすいでしょう。幸いなことに、積分計算機があります。この問題に積分計算機を使うには、リンクをクリックして、上部のテキストボックスに次の値を入力してください:(1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25x/264))^2*exp(-98x/165)/(165/98)。次にオプションをクリックし、下限を0、上限を無限大に設定します。最後に「実行」をクリックします。
積分境界を考慮する前の答えは、(98*(-(165*e^(-(98*x)/165))/98+(2640*e^(-(839*x)/1320))/839+(330*e^(-(109*x)/165))/109-(220*e^(-(149*x)/220))/149+(880*e^(-(303*x)/440))/303-(1760*e^(-(309*x)/440))/309-(11* e^(-(8*x)/11))/8-(1320*e^(-(241*x)/330))/241+(1320*e^(-(491*x)/660))/491-(5280*e^(-(99) 7*x)/1320))/997+(528*e^(-(203*x)/264))/203+(2640*e^(-(1019*x)/1320))/1019-(60*e^(-(47*x) )/60))/47+(2640*e^(-(263*x)/330))/263-(132*e^(-(107*x)/132))/107+(528*e^(-(217*x)/264) )/217+(80*e^(-(33*x)/40))/33-(1760*e^(-(369*x)/440))/369+(40*e^(-(17*x)/20))/17-(88*e^( -(19*x)/22))/19-(15*e^(-(13*x)/15))/13-(480*e^(-(107*x)/120))/107+(528*e^(-(239*x)/264) )/239-(12*e^(-(11*x)/12))/11+(15*e^(-(14*x)/15))/7+(48*e^(-(23*x)/24))/23-e^(-x)))/165。
幸いなことに、その計算機は積分境界を考慮しており、解は 3700403899126040038831518494284887738125 / 22780863797678919004236184338193605974839452 となり、これはおよそ 0.0001624347492698264 に等しくなります。
もちろん、これは6点すべてを獲得する確率ですが、同じロジックを使って任意の数の点を獲得する確率を求めることができます。これは読者の皆さんの課題として残しておきます ;-)。
外部リンク
- ファイアベットの計算については、私の関連サイトWizard of Vegasで議論されています。
- 誰でもダウンロードできるように GoogleDocs に投稿した私自身のスプレッドシートをご覧ください。
- Stwart N. Ethier 著の「The Doctrine of Chances: Probabilistic Aspects of Gambling」には、Fire Bet の数学に関する議論があります。
謝辞
積分法を使用して Fire Bet の確率を解く方法について、たゆまぬアドバイスをくれた Wizard of Vegas フォーラム メンバーの Ace2 に感謝します。



