このページ
キノ爆発
概要
キノエクスプロージョンはIGTのキノのバリエーションゲームです。プレイヤーが選択していない3つの数字に爆弾を配置します。ボールが爆弾の数字と一致すると爆発し、爆発の破片がプレイヤーが選択した数字に当たるとヒットとなります。
ルール
- プレイヤーは 1 から 80 までの数字を 2 から 10 個選びます。
- ゲームはプレイヤーが選択しなかった 3 つの数字をランダムに選択し、爆弾でマークします。
- このゲームでは、1 から 80 までの 20 個の数字を置き換えずに抽選します。
- ゲームによって抽選されたボールがプレイヤーの選択した数字と一致した場合、それは「キャッチ」としてカウントされます。
- ゲームで抽選されたボールが爆弾でマークされた3つの数字のいずれかに当たった場合、その爆弾は爆発します。爆発後、1~3個の破片がゲームで選ばれなかった、または爆弾でマークされていない57個の数字のいずれかに落ちます。
- 1 つの数字に 2 つ以上の破片が当たることはありません。
- 爆弾の破片がプレイヤーが選んだ数字に当たった場合も、「キャッチ」としてカウントされます。
- 27 個の爆弾の小規模なサンプルに基づくと、爆弾 1 個あたりの破片の平均数は 1.85 個です。
- プレイヤーにはキャッチ数と掲示された支払表に従って支払いが行われます。
- 以下の配当表は、ラスベガスのレッド ロック カジノで 10 セント賭けた場合の単なる例です。
ルールが分かりにくい場合は、ルール画面のスクリーンショットをご覧ください。どちらかの画像をクリックすると拡大表示されます。
 | 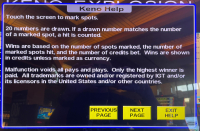 |
以下の表はペイテーブルの例です。多くのペイアウトは0.5で終わることに注意してください。ペイアウトの合計を端数に収めるには、プレイヤーは偶数枚のコインを賭ける必要があります。
キノエクスプロージョンのペイテーブル
| キャッチ | 2つ目を選ぶ | 3つ選ぶ | 4つ選ぶ | 5つ選ぶ | 6つ選ぶ | 7つ選ぶ | 8つ選ぶ | 9番を選ぶ | 10個選ぶ |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 12 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 32.5 | 3.5 | 2 | 1.5 | 0.5 | 0 | 0 | 0 | |
| 4 | 107 | 12.5 | 4 | 1.5 | 1 | 0.5 | 0 | ||
| 5 | 450 | 53 | 13 | 7 | 3 | 2.5 | |||
| 6 | 1000 | 217 | 54 | 23 | 12 | ||||
| 7 | 3750 | 835 | 171 | 77 | |||||
| 8 | 5000 | 2400 | 505 | ||||||
| 9 | 5000 | 2300 | |||||||
| 10 | 5000 |
例
下の画像は、私が44、45、46、54、55、56の6つの数字を選んだゲームの様子です。爆弾は1、36、41に置かれました。この画像はボール抽選後、爆弾が爆発する前のものです。爆弾が爆発する前に、6つの数字のうち4つを当て、8倍の配当を得ていることに注目してください。
上の画像は爆弾が爆発した後に撮影したものです。爆弾の破片が21、38、55、77に当たりました。これらの数字の背景が赤く、燃えているように見えるので、それが分かります。以前爆弾が置かれていた数字、1、36、41は、壊れているように見えます。破片の1つは、私が選んだ数字の一つである55に当たりました。これにより、キャッチ数が4から5に増え、勝利数も8から106に増えました。
爆弾は爆発するように仕掛けられているのか?
以下の表は、20個のボールの中から0個から3個の爆弾がゲームでキャッチされる確率を示しています。これは、各爆弾がボールのドローに一致する確率が20/80 = 25%であると仮定した場合のものです。3個の爆弾すべてがボールのドローに一致する確率は0.013875であることに留意してください。
予想される爆弾爆発
| 爆弾 キャッチ | 組み合わせ | 確率 |
|---|---|---|
| 3 | 1140 | 0.013875 |
| 2 | 11400 | 0.138754 |
| 1 | 35400 | 0.430867 |
| 0 | 34220 | 0.416504 |
| 合計 | 82160 | 1.000000 |
以下の表は、208試合のうち少数のサンプルにおいて、ドローによってヒットされた爆弾の数を示しています。右の列は、208試合における爆弾キャッチ数に基づいて、予想される試合数を示しています。
爆弾捕獲サンプル
| 爆弾 キャッチ | サンプル 観察 | 期待される |
|---|---|---|
| 3 | 30 | 2.89 |
| 2 | 34 | 28.86 |
| 1 | 25 | 89.62 |
| 0 | 119 | 86.63 |
| 合計 | 208 | 208.00 |
208回のゲームのうち、30回は3つの爆弾すべてが爆発しました。もしゲームが自然オッズに従っていたとしたら、3つの爆弾すべてが爆発するゲームの期待値は2.89回になります。
208試合中、30個以上の爆弾が爆発する確率は、期待値から17.78標準偏差離れています。30個以上の爆弾が観測される確率は、20,840,430,698,432,300,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000分の1です。
上記の観察結果と期待値に対するカイ二乗検定では、結果が 12,703,492,578,520,200,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 分の 1 以上歪む確率があります。
最初のルール画面には、「爆発と破片はすべての数字が抽選された後に評価されます」と記載されていることに注目すべきです。これは解釈の余地はありますが、爆弾に関するすべての出来事は必ずしもランダムなボールの抽選によって決定されるのではなく、独立して決定されることを示唆しています。
このゲームがギャフされた場合、それはプレイヤーに有利なギャフであることを強調したいと思います。しかし、どちらの方向のギャフもネバダ州改正法14.040.5に違反すると主張します。同法は、「ライブギャンブルゲームを再現するゲーム機器の場合、ゲーム結果にシンボルまたはその他の要素が出現する数学的確率は、ライブギャンブルゲームでそのシンボルまたは要素が出現する数学的確率と等しくなければならない」と規定しています。
このゲームをあらゆる面で自然なオッズを仮定したランダムシミュレーションで計算したところ、リターンは82.49%でした。私の知る限り、このゲームのメーカーであるIGTは最低85%の設定しか許可していません。レッドロックにある同じマシンでプレイした他の5セントキノゲームの平均リターンは89.45%でした。これは、このゲームがギャフゲームであり、すべての数字が均等に出る自然なボールドローよりも、ボールドローで爆弾が出る可能性が高いというさらなる証拠です。
ビデオ
このビデオでは、Keno Explosion がライブ キーノの自然な確率に一致しない理由について、私の証拠と議論を紹介します。




