このページ
対戦ポーカー
導入
Opponent Poker は、2006 年 12 月 17 日に Red Rock Resort で私が気づいたビデオ ポーカーのバリエーションです。最初の 5 クレジットの賭けは通常のビデオ ポーカーのようにプレイし、次の 5 クレジットは 2 人のコンピュータ対戦相手とプールされ、最高のビデオ ポーカー ハンドが全てを獲得します。
ルール
- プレイヤーは 0、1、2、3、4、5、または 10 クレジットを賭けることができます。
- プレイヤーが 5 クレジット以下を賭けた場合、ゲームは通常のビデオポーカーのようにプレイされます。
- プレイヤーが10クレジットを賭けた場合、そのうち5クレジットは通常のビデオポーカーの賭けとして扱われます。残りの5クレジットは、2人のコンピュータープレイヤーとの対戦に使用されます。
- 10クレジットを賭けた場合、最初の5枚のカードが配られた後、両方のコンピューター対戦相手はどちらのカードを保持するかを示します。ゲームのルールによると、対戦相手の戦略は「標準的なポーカー戦略」です。私はこの戦略を知りませんが、Opponent Pokerを自分でプレイした経験からすると、通常は最適なビデオポーカー戦略ですが、常に最適な戦略とは限りません。
- プレイヤーは保持したいカードを選択します。
- プレイヤーと両方の対戦相手には、同じ 52 枚のカードのデッキから交換用のカードが配られます。
- プレイヤーが他の 2 人のコンピュータ対戦相手よりも高い配当のビデオ ポーカー ハンドを持っている場合、そのプレイヤーは 3 つのハンドすべてからビデオ ポーカーの賞金を獲得します。
- 2 人または 3 人の参加者がビデオ ポーカーの最高配当ハンドで同点になった場合、ビデオ ポーカーの賞金の合計は次のハンドに繰り越されます。
- ハンドが同点の場合、プレイヤーはポットを分割することができます。分割されたポットは最も近いクレジットに切り捨てられます。
- ロイヤルフラッシュが配られた場合、プレイヤーがキャッシュアウトした場合、またはプレイヤーがゲームを切り替えた場合、ポットは自動的に分割されます。
戦略
コンピュータ対戦相手の「標準的なポーカー戦略」が何なのか分からないので、プレイヤーの最適な戦略を定量化することはできません。プレイヤーが与えられたペイテーブルに最適なビデオポーカー戦略に従えば、従来のビデオポーカーよりもリターンが高くなるだろうと私は考えています。プレイヤーは常にコンピュータ対戦相手と同じようにプレイするべきではありません。例えば、配られたハンドはKでした。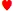 あ
あ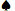 質問
質問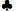 8
8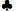 9
9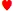 コンピュータの対戦相手は両方ともクイーン、キング、エースを持っていました。ビデオポーカーの最適な戦略は、キングとクイーンのみを持つことです。コンピュータの対戦相手と同じカードを持っている場合、従来のビデオポーカーと同じ期待値になります。この場合、3枚のハイカードを持っている場合の期待値は4.560592クレジット(ビデオポーカーと対戦相手のベットでそれぞれ2.280296クレジット)です。クイーンとキングのみを持っている場合の期待値は4.863301クレジット(ビデオポーカーのハンドで2.397471、対戦相手のベットで2.46583)です。これは、(1)対戦相手が常に最適なビデオポーカー戦略に従うとは限らないこと、(2)対戦相手と常に同じようにプレイするべきではないことを示しています。
コンピュータの対戦相手は両方ともクイーン、キング、エースを持っていました。ビデオポーカーの最適な戦略は、キングとクイーンのみを持つことです。コンピュータの対戦相手と同じカードを持っている場合、従来のビデオポーカーと同じ期待値になります。この場合、3枚のハイカードを持っている場合の期待値は4.560592クレジット(ビデオポーカーと対戦相手のベットでそれぞれ2.280296クレジット)です。クイーンとキングのみを持っている場合の期待値は4.863301クレジット(ビデオポーカーのハンドで2.397471、対戦相手のベットで2.46583)です。これは、(1)対戦相手が常に最適なビデオポーカー戦略に従うとは限らないこと、(2)対戦相手と常に同じようにプレイするべきではないことを示しています。
戻る
戦略セクションで述べたように、私は「標準的なポーカー戦略」を知りません。そのため、完璧な戦略も最大リターンも定量化できません。レッドロックリゾートで観察したビデオポーカーテーブルのリターン表を示すことしかできません。ただし、最大リターンは下記のリターンよりもわずかに高いと考えています。
「9/5」ジャックス・オア・ベター
| 手 | 精算 | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ロイヤルフラッシュ | 800 | 496237776 | 0.000025 | 0.019916 |
| ストレートフラッシュ | 50 | 2137447980 | 0.000107 | 0.005362 |
| 4枚揃い | 25 | 47100799404 | 0.002363 | 0.059073 |
| フルハウス | 9 | 229510637676 | 0.011514 | 0.103626 |
| フラッシュ | 5 | 217120426644 | 0.010892 | 0。054462 |
| 真っ直ぐ | 4 | 223861063908 | 0.011231 | 0.044922 |
| 3つ揃い | 3 | 1484332642620 | 0.074465 | 0.223396 |
| 2組 | 2 | 2577431192796 | 0.129303 | 0.258606 |
| ジャック以上 | 1 | 4288342040640 | 0.215135 | 0.215135 |
| 何もない | 0 | 10862898027756 | 0.544964 | 0.000000 |
| 合計 | 0 | 1.000000 | 0.984498 |
「8/5」ボーナスポーカーデラックス
| 手 | 精算 | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ロイヤルフラッシュ | 800 | 491855652 | 0.000025 | 0.019740 |
| ストレートフラッシュ | 50 | 2154130740 | 0.000108 | 0.005403 |
| 4枚揃い | 80 | 47005788324 | 0.002358 | 0.188653 |
| フルハウス | 8 | 228890564676 | 0.011483 | 0.091863 |
| フラッシュ | 5 | 216493699248 | 0.010861 | 0.054305 |
| 真っ直ぐ | 4 | 260258167080 | 0.013056 | 0.052226 |
| 3つ揃い | 3 | 1475243948064 | 0.074009 | 0.222028 |
| 2組 | 1 | 2556435840408 | 0.128250 | 0.128250 |
| ジャック以上 | 1 | 4216703051664 | 0.211541 | 0.211541 |
| 何もない | 0 | 10929553471344 | 0.548308 | 0.000000 |
| 合計 | 19933230517200 | 1.000000 | 0.974009 |
「9/5」ダブルダブルボーナス — 97.87%
| 手 | 精算 | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ロイヤルフラッシュ | 800 | 497516688 | 0.000025 | 0.019967 |
| ストレートフラッシュ | 50 | 2123092824 | 0.000107 | 0.005326 |
| 4エース + 2-4 | 400 | 1228310184 | 0.000062 | 0.024648 |
| 4 2-4 + A-4 | 160 | 2854473252 | 0.000143 | 0.022912 |
| 4枚のエース + 5枚のK | 160 | 3459809880 | 0.000174 | 0.027771 |
| 4 2-4 + 5-K | 80 | 7662852888 | 0.000384 | 0.030754 |
| 4 5-K | 50 | 32536223652 | 0.001632 | 0.081613 |
| フルハウス | 9 | 216639836640 | 0.010868 | 0.097814 |
| フラッシュ | 5 | 218785162368 | 0.010976 | 0.054880 |
| 真っ直ぐ | 4 | 257980198392 | 0.012942 | 0.051769 |
| 3つ揃い | 3 | 1501776975600 | 0.075340 | 0.226021 |
| 2組 | 1 | 2454744788496 | 0.123148 | 0.123148 |
| ジャック以上 | 1 | 4227940545588 | 0.212105 | 0.212105 |
| 何もない | 0 | 11005000730748 | 0.552093 | 0.000000 |
| 合計 | 0 | 19933230517200 | 1.000000 | 0.978729 |
デュースワイルド — 97.58%
| 手 | 精算 | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ナチュラルロイヤルフラッシュ | 800 | 452258388 | 0.000023 | 0.018151 |
| 4つのデュース | 200 | 3681116136 | 0.000185 | 0.036934 |
| ワイルドロイヤルフラッシュ | 20 | 35519655168 | 0.001782 | 0.035639 |
| 5枚の同じもの | 12 | 59450103984 | 0.002982 | 0.035790 |
| ストレートフラッシュ | 10 | 109163645748 | 0.005476 | 0.054765 |
| フォー・オブ・ア・カインド | 4 | 1213460173776 | 0.060876 | 0.243505 |
| フルハウス | 4 | 520454143512 | 0.026110 | 0.104439 |
| フラッシュ | 3 | 420473233680 | 0.021094 | 0.063282 |
| 真っ直ぐ | 2 | 1160573109144 | 0.058223 | 0.116446 |
| スリーオブアカインド | 1 | 5318990094612 | 0.266840 | 0.266840 |
| 何もない | 0 | 11091012983052 | 0.556408 | 0.000000 |
| 合計 | 0 | 19933230517200 | 1.000000 | 0.975791 |
このゲームの興味深い点は、ルール上、ポットが無限に増加していく可能性があることです。これはネバダ州ゲーミング・コントロール・ボード規則14.2.070に抵触しないようです。同規則では、最高額のジャックポットを当てる確率が1億分の1未満の場合は、その確率を目立つように表示しなければならないと定められています。どのハンドでも、最高額はポット+8000クレジット(ロイヤルの場合)で、その確率は649,740分の1です。


