このページ
オーガニックルーレット実験
概要
2016年9月、インターブロック社製のオーガニックルーレットマシンが、ホイールクロッキングを行うプレイヤーに対して積極的な対策を講じているという告発を耳にしました。公正で誠実なギャンブルの擁護者として、私はこの話題に強い関心を抱きました。6ヶ月間にわたり、私はこの件に関する多くの会議に出席し、数千回分のスピンデータを収集しました。このページでは、その調査の経緯をお伝えします。
ゲーム
オーガニックルーレットは、ラスベガスの多くのカジノで見かけます。テーブルゲームと同じように機能します。プレイヤーは約30秒でベットできます。通常、ボールはプレイヤーが1~5秒のベット時間を残して飛び出します。ベットが終了した後も、ボールが着地するまでに数秒かかります。その後、勝利金が支払われ、このプロセスが繰り返されます。開始から終了まで1分強かかります。
申し立て
ボールが発射されてから賭けが終了するまでの時間が十分であれば、ゲームに勝つことが可能です。賭けが終了する前に、ボールとホイールの速度を分析できます。ホイールクロッカーは、ボール、ホイール、そして発射時のホイールの位置を推定することで、ボールがホイールのどこに着地するかを予測できます。
この問題を私に指摘してくれたプレイヤーをS氏と呼ぶことにします。彼によると、レクリエーションプレイヤーはおそらく公平なゲームを楽しめたでしょう。各数字の当選確率は38分の1です。しかし、特定の危険信号が発せられた場合、ゲームは彼が言うところの「脅威モード」に陥るでしょう。ホイールクロッカーの危険信号は、以下の通りであると仮定されました。
- 高額賭け。「高額」がどの程度の金額を指すのかは不明だが、合計20ドルあれば十分だと判断された。
- レイトベット。具体的には、ボールが発射されてからタイムウィンドウが閉じるまでの5秒間です。
- セクションベット。ホイール上の近い数字に賭けるベットです。
ゲームが危険にさらされると、マシンは積極的な対抗手段を取ると言われていました。対抗手段の目的は、ホイールクロッカーが賭けたセクションからボールを遠ざけることでした。これがどのように行われるのかは不明でしたが、S氏はいくつかの仮説を立てていましたが、それは私に教えないよう頼まれました。
S氏はデータとその分析結果を私に共有してくれました。それは確かに私の興味をそそるものでした。しかし、S氏は具体的な内容については何も話さないようにと頼みました。
グローバルゲームエキスポ
この仕事に関わり始めた頃、2016年にラスベガスで開催されたグローバル・ゲーミング・エキスポに参加しました。インターブロックは、その会場で非常に大きく目立つ場所を構えていました。S氏の許可を得て、インターブロックのブースのエンジニアと話をしたいと申し出ました。最初に対応してくれた店員がエンジニアを見つけてきて、近づいてきて自己紹介してくれました。私はオーガニック・ルーレットに似たマシンに案内されましたが、こちらもボールが発射されてから5秒ほどでプレイヤーがベットを終える時間がありました。自己紹介の後、会話はこんな感じでした。要約すると、こんな感じです。
- シャックルフォード:このマシンでは、賭けが打ち切られる数秒前にボールが放出されることに気づきました。
- インターブロック:それで?
- シャックルフォード:ホイールクロッキングチームに対して脆弱だと思いませんか?
- Interblock: その問題については、弊社も十分認識しております。
彼のボディランゲージと口調から、もう何も言わないつもりだということがわかったので、私は時間を割いてくれたことに感謝し、楽しく立ち去りました。
その会話をあなたがどう解釈するかはあなた次第です。
最初の実験
S氏のプレゼンテーションを受けて、何が起こっているのかとても興味をそそられました。まずは、もう一人の関係者(ここではC氏と呼ぶことにします)と一緒に、299回のスピンデータを収集しました。賭け方は、5つの連続した数字にそれぞれ2ドルずつ賭けるというものでした。S氏は、合計10ドルの賭け金でゲームに脅威を与えるのに十分かどうか確信が持てませんでしたが、実験を進める中で、ゲームを怒らせることと、あまりお金を失うことのないように、ちょうど良いバランスだと感じていました。
C氏も私もホイールクロッカーではないので、2スピン前の当選番号がアークの中心になるようにシステマティックに賭けました。目的は、ホイール上の当選位置が、私たちのベッティングアークの中心とどのように比較されるかを確認することでした。
グラフ 1 と表 1 は、中心の賭け位置と当選番号間の各オフセットの頻度を示しています。
png" />表1
| オフセット | 観察 | 期待 |
|---|---|---|
| -18 | 5 | 7.87 |
| -17 | 9 | 7.87 |
| -16 | 13 | 7.87 |
| -15 | 7 | 7.87 |
| -14 | 11 | 7.87 |
| -13 | 12 | 7.87 |
| -12 | 7 | 7.87 |
| -11 | 10 | 7.87 |
| -10 | 8 | 7.87 |
| -9 | 10 | 7.87 |
| -8 | 6 | 7.87 |
| -7 | 8 | 7.87 |
| -6 | 9 | 7.87 |
| -5 | 10 | 7.87 |
| -4 | 3 | 7.87 |
| -3 | 7 | 7.87 |
| -2 | 7 | 7.87 |
| -1 | 6 | 7.87 |
| 0 | 8 | 7.87 |
| 1 | 4 | 7.87 |
| 2 | 4 | 7.87 |
| 3 | 8 | 7.87 |
| 4 | 7 | 7.87 |
| 5 | 4 | 7.87 |
| 6 | 18 | 7.87 |
| 7 | 6 | 7.87 |
| 8 | 9 | 7.87 |
| 9 | 6 | 7.87 |
| 10 | 8 | 7.87 |
| 11 | 4 | 7.87 |
| 12 | 13 | 7.87 |
| 13 | 3 | 7.87 |
| 14 | 8 | 7.87 |
| 15 | 12 | 7.87 |
| 16 | 6 | 7.87 |
| 17 | 7 | 7.87 |
| 18 | 9 | 7.87 |
| 19 | 7 | 7.87 |
| 合計 | 299 | 299.00 |
カイ二乗適合度検定の結果は、カイ二乗統計量45.29、自由度37となります。ランダムゲームでこれよりも歪んだ結果が出る確率は16.5%です。
表2は、最初の実験で中心の数字を中心とする様々なアークサイズに対するガウス検定の結果を示しています。対象とした5つの数字のアークの場合、公平なホイールで期待される当選回数は39.3回です。しかし、実際には29回でした。公平なゲームでこれほど悪い結果、あるいはそれより悪い結果になる確率は3.84%です。
表2
| アークサイズ | 観察 | 期待 | サイズ標準 偏差 | 標準数 偏差 | 確率 |
|---|---|---|---|---|---|
| 1 | 8 | 7.87 | 2.77 | 0.05 | 0.518957 |
| 3 | 18 | 23.61 | 4.66 | -1.20 | 0.114658 |
| 5 | 29 | 39.34 | 5.85 | -1.77 | 0.038417 |
| 7 | 44 | 55.08 | 6.70 | -1.65 | 0.049187 |
| 17 | 124 | 133.76 | 8.60 | -1.14 | 0.128074 |
結果は確かに予想を下回りましたが、ただの不運だった可能性も十分にありました。しかし、もし同じような割合で負け続けるのであれば、不正行為と判断するにはサンプル数を増やすだけで済むだろうと計算しました。何度も会議やメールでやり取りを重ねた結果、2度目の実験を行うことに決定しました。
第二の実験
カジノゲームが公正に行われていないという正当な主張をするには、それを証明する実験は再現可能であるべきです。多くの議論を重ねた結果、5つの数字からなるアークの各数字に5ドルずつ賭け、勝ちの不足を検証することが決定されました。3つの異なるホイールで1,000回スピンすることにしました。S氏のプレイに加え、私かC氏のどちらか、少なくとも1人の目撃者が常にいました。プレイ終了後、データを検証し、次に何をすべきかを決定することにしました。合理的な疑いの余地なく、ランダムではないゲームが行われたと判断された場合は、証拠を公開するつもりでした。
この話の終わりまでに、1,204回のスピンデータがありました。結果は予想より少し劣っていたことは承知していましたが、S氏によると、ゲームはほとんどの場合ランダムに動作し、「脅威」モードになったのはほんの一部だったそうです。
このデータのレビューに基づいて、私たちはプレーを続ける価値があるほど負けていないと感じました。
以下は2回目の実験の結果と分析です。まず、次のグラフと表3は、弧の中心とボールの着地点の間のオフセットの頻度を示しています。
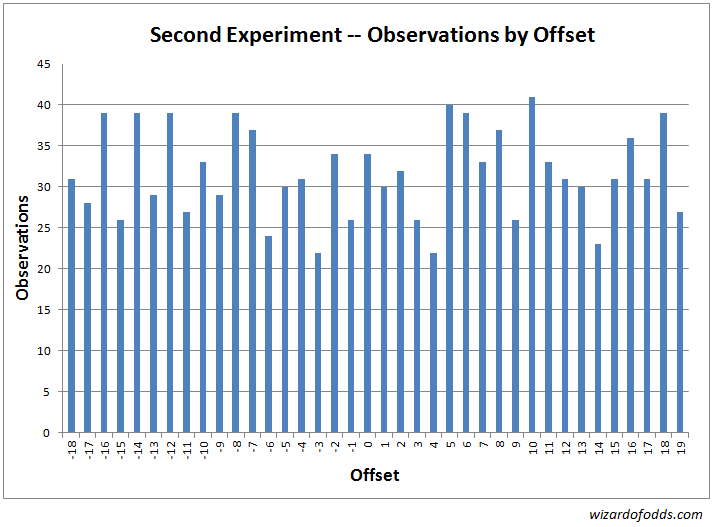
表3
| オフセット | 観察 | 期待 |
|---|---|---|
| -18 | 31 | 31.68 |
| -17 | 28 | 31.68 |
| -16 | 39 | 31.68 |
| -15 | 26 | 31.68 |
| -14 | 39 | 31.68 |
| -13 | 29 | 31.68 |
| -12 | 39 | 31.68 |
| -11 | 27 | 31.68 |
| -10 | 33 | 31.68 |
| -9 | 29 | 31.68 |
| -8 | 39 | 31.68 |
| -7 | 37 | 31.68 |
| -6 | 24 | 31.68 |
| -5 | 30 | 31.68 |
| -4 | 31 | 31.68 |
| -3 | 22 | 31.68 |
| -2 | 34 | 31.68 |
| -1 | 26 | 31.68 |
| 0 | 34 | 31.68 |
| 1 | 30 | 31.68 |
| 2 | 32 | 31.68 |
| 3 | 26 | 31.68 |
| 4 | 22 | 31.68 |
| 5 | 40 | 31.68 |
| 6 | 39 | 31.68 |
| 7 | 33 | 31.68 |
| 8 | 37 | 31.68 |
| 9 | 26 | 31.68 |
| 10 | 41 | 31.68 |
| 11 | 33 | 31.68 |
| 12 | 31 | 31.68 |
| 13 | 30 | 31.68 |
| 14 | 23 | 31.68 |
| 15 | 31 | 31.68 |
| 16 | 36 | 31.68 |
| 17 | 31 | 31.68 |
| 18 | 39 | 31.68 |
| 19 | 27 | 31.68 |
| 合計 | 1204 | 1204.00 |
カイ二乗適合度検定の結果、カイ二乗統計量は34.79、自由度は37となります。ランダムゲームでこれよりも歪んだ結果が出る確率は57.32%です。
表4は、中心の数字を中心とする様々な弧のサイズに対するガウス検定の結果を示しています。すべての弧のサイズは正常範囲内に収まっています。
表4
| アークサイズ | 観察 | 期待 | サイズ標準 偏差 | 標準数 偏差 | 確率 |
|---|---|---|---|---|---|
| 1 | 34 | 31.68421053 | 5.55 | 0.42 | 0.661637 |
| 3 | 90 | 95.05263158 | 9.36 | -0.54 | 0.294599 |
| 5 | 156 | 158.4210526 | 11.73 | -0.21 | 0.418235 |
| 7 | 204 | 221.7894737 | 13.45 | -1.32 | 0.092997 |
| 17 | 536 | 538.6315789 | 17.25 | -0.15 | 0.439385 |
総合結果
以下は、最初の実験と2番目の実験を組み合わせたデータです。まず、次のグラフと表5は、弧の中心とボールの着地点の間の各オフセットの頻度を示しています。
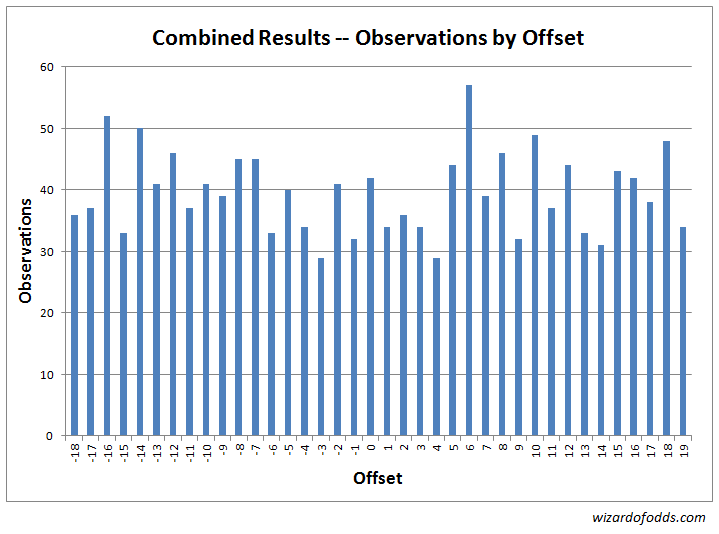
表5
| オフセット | 観察 | 期待 |
|---|---|---|
| -18 | 36 | 39.55 |
| -17 | 37 | 39.55 |
| -16 | 52 | 39.55 |
| -15 | 33 | 39.55 |
| -14 | 50 | 39.55 |
| -13 | 41 | 39.55 |
| -12 | 46 | 39.55 |
| -11 | 37 | 39.55 |
| -10 | 41 | 39.55 |
| -9 | 39 | 39.55 |
| -8 | 45 | 39.55 |
| -7 | 45 | 39.55 |
| -6 | 33 | 39.55 |
| -5 | 40 | 39.55 |
| -4 | 34 | 39.55 |
| -3 | 29 | 39.55 |
| -2 | 41 | 39.55 |
| -1 | 32 | 39.55 |
| 0 | 42 | 39.55 |
| 1 | 34 | 39.55 |
| 2 | 36 | 39.55 |
| 3 | 34 | 39.55 |
| 4 | 29 | 39.55 |
| 5 | 44 | 39.55 |
| 6 | 57 | 39.55 |
| 7 | 39 | 39.55 |
| 8 | 46 | 39.55 |
| 9 | 32 | 39.55 |
| 10 | 49 | 39.55 |
| 11 | 37 | 39.55 |
| 12 | 44 | 39.55 |
| 13 | 33 | 39.55 |
| 14 | 31 | 39.55 |
| 15 | 43 | 39.55 |
| 16 | 42 | 39.55 |
| 17 | 38 | 39.55 |
| 18 | 48 | 39.55 |
| 19 | 34 | 39.55 |
| 合計 | 1503 | 1503.00 |
カイ二乗適合度検定の結果は、カイ二乗統計量41.75、自由度37となります。ランダムゲームでこれよりも歪んだ結果が出る確率は27.19%です。
表6は、中央の数字を中心とする様々な弧の大きさに対するガウス検定の結果を示しています。すべての検定結果は、公正なゲームとして妥当な範囲内に収まっています。
表6
| アークサイズ | 観察 | 期待 | サイズ標準 偏差 | 標準数 偏差 | 確率 |
|---|---|---|---|---|---|
| 1 | 42 | 39.55263158 | 6.21 | 0.39 | 0.653346 |
| 3 | 108 | 118.6578947 | 10時45分 | -1.02 | 0.153986 |
| 5 | 185 | 197.7631579 | 13.11 | -0.97 | 0.165050 |
| 7 | 248 | 276.8684211 | 15.03 | -1.92 | 0.027374 |
| 17 | 660 | 672.3947368 | 19.28 | -0.64 | 0.260114 |
最初の実験と2番目の実験の結果の相関係数は0.153853です。簡単に言えば、わずかな相関関係があったものの、ランダムに抽出された2つのデータセットから予想される範囲内であったことを意味します。
結論
いかなるゲームも、公正なゲームの自然な確率に従ってプレイされていないと断言するには、非常に高い基準の証拠が必要です。今回のケースでは、その基準は満たされていませんでした。言い換えれば、オーガニックルーレットマシンが不公平にプレイされていると非難する正当な根拠は私にはありません。
回答
S氏には、このページを一般公開する前にプレビューする機会を提供しました。彼は多くの有益な提案と修正をしてくれました。しかし、最終的に私の表現方法にまだいくつか問題があったため、私は彼に回答を公開する機会を与えました。そして彼はそれに応じてくれました。そのタイトルは「S氏によるインターブロック実験結果に関する別の視点」です。
私はいつも最後まで発言したいので、「マイケル・シャックルフォードのオーガニックルーレット実験に対するS氏の回答への回答」と題した反論記事を公開しました。



