このページ
テキサスシュートアウト
概要
テキサスシュートアウトは、 Galaxy Gamingによるシンプルなポーカーゲームです。プレイヤーとディーラーが対戦し、より強いハンドを持つ方が勝ちます。決めなければならないのは、最初に4枚のカードのうちどの2枚を出すかだけです。プレイヤーの強みは、自由に選択できることとスプリットできることです。ディーラーの強みは、引き分けで勝つことです。プレイしやすく、ボラティリティが低く、競争力のあるハウスエッジを持つポーカーゲームをお探しなら、テキサスシュートアウトはきっと楽しめるでしょう。
ルール
- このゲームは、通常の52枚のカード6組からなるシューでプレイされます。すべてのハンドは、従来のポーカールールに従って採点されます。
- プレイヤーはポーカーの賭けに加えて、オプションでサイドベットを行います。
- プレイヤーとディーラーの両方に4枚のカードが裏向きで配られます。プレイヤーは自分のカードを確認することができます。
- プレイヤーは、(A) 4枚のカードのうち2枚を選び、残りの2枚を捨てるか、(B) 2枚のカードからなるハンドを2つに分割するかを選択できます。分割する場合は、ポーカーベットとサイドベット(ある場合)を同額ずつ賭けなければなりません。
- ディーラーはカードをめくり、以下のハウスウェイに従って最初に 2 枚のカードを選択し、残りの 2 枚のカードを捨てます。
- ディーラーは5枚のコミュニティカードを配ります。
- プレイヤーとディーラーの両方が、5 枚のコミュニティ カードと 2 枚のホール カードから任意の 5 枚のカードを使用して、最高の 5 枚のポーカー ハンドを作成する必要があります。
- プレイヤーの手札がより高い場合、プレイヤーは同額の賞金を獲得します。ディーラーの手札がより高い場合、または同点の場合は、ディーラーが勝ちます。
- サイドベットの配当は、プレイヤーの5枚のカードの合計値と以下のペイテーブルのいずれかに基づいて決定されます。ペイテーブル2が最も一般的に使用されていると思います。さらに、以下に示すように、テーブルにいる他のプレイヤー全員のポーカーバリューに基づいて「エンヴィボーナス」が付与されます。
ディーラーは、以下のリストの中で最も高いランクの2枚のカードをプレイします。同じランクのカードが2つある場合は、ディーラーはより高いランクのカードをプレイします。各ハンドの例は、各ルールの後に示します。
- 8以上のペア。Q
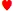 、 Q
、 Q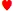
- ハイカードはエース、ローカードはジャック以上です。
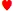 、Q
、Q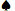
- 2から7までのスーツドペア。6
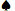 、6
、6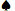
- 2から7までのアンスーツペア。6
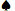 、 6
、 6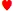
- エースハイとスーツ。A
 、 4
、 4
- 両方のカードが10以上でスーツが同じ。K
 、 10
、 10
- 両方のカードが10以上で、スーツが異なります。K
 、10
、10
- エースハイアンスーテッド。A
 、4
、4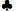
- 絵札ハイスーテッド。J
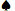 、7
、7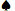
- 絵札ハイ、アンスーテッド。J
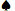 、 7
、 7
- 繋がったカードのスーツ。4
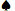 、5
、5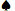
- 繋がったカードはスートが違います。6
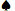 、 7
、 7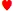
- 最も強いスーツの2枚のカード。8
 、3
、3
- スーツが異なる2枚の最も高いカード。9
 、 7gif">
、 7gif">
サイドベットの配当表
| 手 | 給与表1 | 給与表2 | 給与表3 |
|---|---|---|---|
| 5枚の同じスーツ | 5000対1 | 1000対1 | 1000対1 |
| ロイヤルフラッシュ | 500対1 | 200対1 | 200対1 |
| ストレートフラッシュ | 100対1 | 75対1 | 75対1 |
| 5枚の同じもの | 50対1 | 40対1 | 40対1 |
| フォー・オブ・ア・カインド | 5対1 | 7対1 | 7対1 |
| フルハウス | 3対1 | 3対1 | 3対1 |
| フラッシュ | 2対1 | 2対1 | 2対1 |
| 真っ直ぐ | 1対1 | 1対1 | 2対1 |
| スリーオブアカインド | 失う | 押す | 押す |
羨望ボーナス
| 手 | 支払う |
|---|---|
| 5枚の同じスーツ | 1000ドル |
| ロイヤルフラッシュ | 250ドル |
| ストレートフラッシュ | 50ドル |
| 5枚の同じもの | 10ドル |
戦略
以下の戦略は必ずしも最適ではありません。ペナルティカードの状況によっては、プレイヤーの勝率がわずかに上昇する可能性があります。
プレイヤーは、以下のリストで最も高いランクの2枚のカードをプレイすべきです。残りの2枚のカードが期待値が0より大きい(ランク26以上)ハンドを形成する場合、プレイヤーはスプリットしてそのハンドもプレイすべきです。このリストの期待値は大まかなものであり、ハンドの順番を示すことのみを目的としています。以下の表は、プレイヤーがサイドベットを行わないことを前提としています。もしサイドベットを行った場合、戦略は大きく変わります。
2枚のカードのハンドランキング
| ランク | 手 | 期待値 |
|---|---|---|
| 1 | スーツA | 0.575301 |
| 2 | スートなしのA | 0.553041 |
| 3 | スーツK | 0.490895 |
| 4 | アンスートK | 0.464249 |
| 5 | スーツQ | 0.417272 |
| 6 | アンスートQ | 0.386637 |
| 7 | スーツJ | 0.345383 |
| 8 | アンスートJ | 0.311134 |
| 9 | スーツ10 | 0.275898 |
| 10 | アンスート10 | 0.237068 |
| 11 | スーツ9 | 0.205034 |
| 12 | スートのない9 | 0.162011 |
| 13 | スーツ8 | 0.154705 |
| 14 | スーテッドA、K | 0.109348 |
| 15 | アンスーツ8 | 0.107616 |
| 16 | スーツ7 | 0.106813 |
| 17 | スーテッドA、Q | 0.069761 |
| 18 | スーツ6 | 0.05977 |
| 19 | アンスート7 | 0.055731 |
| 20 | アンスートA、K | 0.053211 |
| 21 | スーツA、J | 0.033959 |
| 22 | スーツ5 | 0.013691 |
| 23 | スーツK、Q | 0.012594 |
| 24 | スイートA、10 | 0.011557 |
| 25 | アンスートA、Q | 0.010262 |
| 26 | アンスーツ6 | 0.005561 |
| 27 | スーツK、J | -0.0187 |
| 28 | アンスートA、J | -0.029408 |
| 29 | スーツ4 | -0.033235 |
| 30 | スーツA、9 | -0.039459 |
| 31 | アンスーテッド5 | -0.04346 |
| 32 | スイートK、10 | -0.044542 |
| 33 | アンスーテッドK、Q | -0.048566 |
| 34 | アンスートA,10 | -0.053852 |
| 35 | スーツA、8 | -0.060539 |
| 36 | スーテッドQ、J | -0.063067 |
| 37 | スーツ3 | -0.078173 |
| 38 | スートA、7 | -0.0806 |
| 39 | アンスートK、J | -0.082504 |
| 40 | スーツQ,10 | -0.088102 |
| 41 | スーツK、9 | -0.089785 |
| 42 | アンスート4 | -0.093836 |
| 43 | スートA、6 | -0.100855 |
| 44 | スーツA、5 | -0.10132 |
| 45 | 不適合A,9 | -0.110164 |
| 46 | スーツなしK、10 | -0.11166 |
| 47 | スートA、4 | -0.116193 |
| 48 | スーツJ、10 | -0.122052 |
| 49 | スーツ2 | -0.122698 |
| 50 | スーツK、8 | -0.124103 |
| 51 | アンスートQ,J | -0.127974 |
| 52 | スーツQ、9 | -0.12845 |
| 53 | スーツA、3 | -0.131083 |
| 54 | アンスートA,8 | -0。131953 |
| 55 | スーツK、7 | -0.139746 |
| 56 | アンスーテッド3 | -0.142697 |
| 57 | スーツA、2 | -0.145134 |
| 58 | アンスートA,7 | -0.154346 |
| 59 | 不適合Q,10 | -0.155267 |
| 60 | スーツK、6 | -0.15593 |
| 61 | スーツJ、9 | -0.159122 |
| 62 | アンスートK、9 | -0.160559 |
| 63 | スーツQ,8 | -0.161784 |
| 64 | スーツK、5 | -0.170875 |
| 65 | アンスートA,6 | -0.176551 |
| 66 | アンスートA,5 | -0.17671 |
| 67 | スーツ 10,9 | -0.180637 |
| 68 | スーツK、4 | -0.185425 |
| 69 | アンスート J,10 | -0.189734 |
| 70 | アンスーツ2 | -0.191214 |
| 71 | スーツJ、8 | -0.191644 |
| 72 | アンスートA,4 | -0.193476 |
| 73 | スーツQ、7 | -0.194186 |
| 74 | アンスートK、8 | -0.197604 |
| 75 | スーツK、3 | -0.199133 |
| 76 | 不適合Q,9 | -0.199229 |
| 77 | スーツQ、6 | -0.206405 |
| 78 | アンスートA,3 | -0.209351 |
| 79 | スーツ10,8 | -0.2107 |
| 80 | スーツK、2 | -0.213633 |
| 81 | アンスートK、7 | -0.214514 |
| 82 | スーツ9,8 | -0.217352 |
| 83 | スーツQ,5 | -0.220169 |
| 84 | スートJ、7 | -0.223077 |
| 85 | アンスートA,2 | -0.22489 |
| 86 | アンスート J,9 | -0.22991 |
| 87 | アンスートK、6 | -0.232094 |
| 88 | スーツQ、4 | -0.235311 |
| 89 | 非スートQ,8 | -0.235583 |
| 90 | スーツ9,7 | -0.240067 |
| 91 | スーツ10,7 | -0.240998 |
| 92 | スーツ8,7 | -0.24438 |
| 93 | アンスートK、5 | -0.248762 |
| 94 | スーツQ、3 | -0.249074 |
| 95 | 不適合 10,9 | -0.251406 |
| 96 | スートJ、6 | -0.252745 |
| 97 | スーツQ,2 | -0.262805 |
| 98 | スーツJ、5 | -0.263285 |
| 99 | アンスートK、4 | -0.264611 |
| 100 | アンスート J,8 | -0.265759 |
| 101 | スーツ8,6 | -0.266064 |
| 102 | スーツ9,6 | -0.266234 |
| 103 | スーツ7,6 | -0.268436 |
| 104 | スーツ10,6 | -0.270272 |
| 105 | 非スートQ,7 | -0.270629 |
| 106 | スートJ、4 | -0.27729 |
| 107 | アンスートK、3 | -0.279442 |
| 108 | 非スートQ,6 | -0.283973 |
| 109 | 不適合 10,8 | -0.284135 |
| 110 | 不適合 9,8 | -0.290229 |
| 111 | スーツJ、3 | -0.290602 |
| 112 | スーツ7.5 | -0.291758 |
| 113 | スーツ6,5 | -0.292394 |
| 114 | スーツ9.5 | -0.29242 |
| 115 | スーツ8.5 | -0.292459 |
| 116 | アンスートK、2 | -0.295417 |
| 117 | スーツ10,5 | -0.298923 |
| 118 | 非スートQ,5 | -0.29957 |
| 119 | アンスート J,7 | -0.299933 |
| 120 | スーツJ、2 | -0.304647 |
| 121 | スーツ10,4 | -0.309336 |
| 122 | スーツ5,4 | -0。314195 |
| 123 | 不適合 9,7 | -0.315221 |
| 124 | 非スートQ,4 | -0.315476 |
| 125 | 不適合 10,7 | -0.317375 |
| 126 | スーツ6,4 | -0.318104 |
| 127 | アンスート 8,7 | -0.318633 |
| 128 | スーツ7,4 | -0.3204 |
| 129 | スーツ8,4 | -0.321035 |
| 130 | スーツ9,4 | -0.321037 |
| 131 | スーツ10,3 | -0.322631 |
| 132 | スーツ9,3 | -0.329597 |
| 133 | 非スートQ,3 | -0.33053 |
| 134 | アンスート J,6 | -0.331918 |
| 135 | スーツ10,2 | -0.335747 |
| 136 | スーツ5,3 | -0.340684 |
| 137 | スーツ9,2 | -0.342481 |
| 138 | 不適合 9,6 | -0.342769 |
| 139 | アンスート 8,6 | -0.34313 |
| 140 | アンスート J,5 | -0.343243 |
| 141 | アンスート 7,6 | -0.34495 |
| 142 | 非スートQ,2 | -0.346033 |
| 143 | スーツ6,3 | -0.347068 |
| 144 | 不適合 10,6 | -0.348636 |
| 145 | スーツ7,3 | -0.348941 |
| 146 | スーツ8,3 | -0.349902 |
| 147 | アンスート J,4 | -0.358831 |
| 148 | スーツ4,3 | -0.358841 |
| 149 | スーツ8,2 | -0.359102 |
| 150 | スーツ5,2 | -0.369618 |
| 151 | アンスート 7,5 | -0.370327 |
| 152 | アンスート 6,5 | -0.370589 |
| 153 | アンスート 9.5 | -0.371722 |
| 154 | アンスート 8,5 | -0.371759 |
| 155 | アンスート J,3 | -0.373192 |
| 156 | スーツ6,2 | -0.376459 |
| 157 | スーツ7,2 | -0.377908 |
| 158 | アンスート 10,5 | -0.37939 |
| 159 | スーツ4,2 | -0.384973 |
| 160 | アンスート J,2 | -0.388862 |
| 161 | 不適合 10,4 | -0.390903 |
| 162 | アンスート 5,4 | -0.39378 |
| 163 | アンスート 6,4 | -0.398771 |
| 164 | アンスート 7,4 | -0.401385 |
| 165 | スーツ3,2 | -0.401451 |
| 166 | 不適合 9,4 | -0.402623 |
| 167 | アンスート 8,4 | -0.402719 |
| 168 | 不適合 10,3 | -0.40569 |
| 169 | 不適合 9,3 | -0.412853 |
| 170 | 不適合 10,2 | -0.420634 |
| 171 | アンスート 5,3 | -0.422846 |
| 172 | 不適合 9,2 | -0.427508 |
| 173 | アンスート 6,3 | -0.430175 |
| 174 | アンスート 7,3 | -0.432623 |
| 175 | アンスート 8,3 | -0.433916 |
| 176 | 不適合 4,3 | -0.442055 |
| 177 | 不適合 8,2 | -0.444371 |
| 178 | アンスート 5,2 | -0.454349 |
| 179 | アンスート 6,2 | -0.462125 |
| 180 | アンスート 7,2 | -0.464479 |
| 181 | 不適合 4,2 | -0.470729 |
| 182 | アンスート 3,2 | -0.488024 |
分析
各イニシャルハンドには5つの結果が考えられます。ほとんどの場合、プレイヤーは1ユニットの勝ちか負けとなります。プレイヤーがスプリットした場合、2ユニットの勝ち、引き分け、または2ユニットの負けのいずれかとなります。以下の表は、イニシャルハンドごとのすべてのネット勝利の可能性とリターンを示しています。右下のセルはハウスエッジが2.57%であることを示しています。
ポーカーのベットリターン表
| 勝つ | 確率 | 戻る |
|---|---|---|
| 2 | 0.026618 | 0.053236 |
| 1 | 0.437762 | 0.437762 |
| 0 | 0.032391 | 0 |
| -1 | 0.489783 | -0.489783 |
| -2 | 0.013445 | -0.026891 |
| 合計 | 1 | -0.025675 |
プレイヤーは7.25%の確率でスプリットします。つまり、リスク要素は2.57%/1.0725 = 2.39%となります。
次の3つのリターン表は、Envyボーナスを考慮する前のサイドベットの3つの可能なペイテーブルを示しています。表の確率は、プレイヤーが上記の戦略に従うことを前提としています。この戦略は、ポーカーベットのみを行うプレイヤー向けに設計されています。もしプレイヤーがサイドベットを行った場合、私が知らない戦略調整を行うことで、ポーカーベットを犠牲にしてサイドベットからより多くのバリューを得る可能性があります。しかし、私の経験から判断すると、そのような戦略調整によるメリットはわずかです。ペイテーブル3を使用するフルテーブルでプレイする場合を除き、サイドベットは行わないことをお勧めします。
サイドベット配当表1
| 手 | 支払う | 確率 | 戻る |
|---|---|---|---|
| 5枚の同じスーツ | 5000対1 | 0.000001 | 0.004175 |
| ロイヤルフラッシュ | 500対1 | 0.000082 | 0.040866 |
| ストレートフラッシュ | 100対1 | 0.000203 | 0.020345 |
| 5枚の同じもの | 50対1 | 0.001213 | 0.060651 |
| フォー・オブ・ア・カインド | 5対1 | 0.020021 | 0.100103 |
| フルハウス | 3対1 | 0.084969 | 0.254907 |
| フラッシュ | 2対1 | 0.050618 | 0.101237 |
| 真っ直ぐ | 1対1 | 0.031316 | 0.031316 |
| スリーオブアカインド | -1対1 | 0.098834 | -0.098834 |
| その他すべて | -1対1 | 0.712743 | -0.712743 |
| 合計 | 1 | -0.197977 |
サイドベット配当表2
| 手 | 支払う | 確率 | 戻る |
|---|---|---|---|
| 5枚の同じスーツ | 1000対1 | 0.000001 | 0.000835 |
| ロイヤルフラッシュ | 200対1 | 0.000082 | 0.016346 |
| ストレートフラッシュ | 75対1 | 0.000203 | 0.015259 |
| 5枚の同じもの | 40対1 | 0.001213 | 0.04852 |
| フォー・オブ・ア・カインド | 7対1 | 0.020021 | 0.140145 |
| フルハウス | 3対1 | 0.084969 | 0.254907 |
| フラッシュ | 2対1 | 0.050618 | 0.101237 |
| 真っ直ぐ | 1対1 | 0.031316 | 0.031316 |
| スリーオブアカインド | 押す | 0.098834 | 0 |
| その他すべて | -1対1 | 0.712743 | -0.712743 |
| 合計 | 1 | -0.104177 |
サイドベット配当表3
| 手 | 支払う | 確率 | 戻る |
|---|---|---|---|
| 5枚の同じスーツ | 1000対1 | 0.000001 | 0.000835 |
| ロイヤルフラッシュ | 200対1 | 0.000082 | 0.016346 |
| ストレートフラッシュ | 75対1 | 0.000203 | 0.015259 |
| 5枚の同じもの | 40対1 | 0.001213 | 0.04852 |
| フォー・オブ・ア・カインド | 7対1 | 0.020021 | 0.140145 |
| フルハウス | 3対1 | 0.084969 | 0.254907 |
| フラッシュ | 2対1 | 0.050618 | 0.101237 |
| 真っ直ぐ | 2対1 | 0.031316 | 0.062632 |
| スリーオブアカインド | 押す | 0.098834 | 0 |
| その他すべて | -1対1 | 0.712743 | -0.712743 |
| 合計 | 1 | -0.072861 |
最後の表は、Envyボーナスを考慮したサイドベットのハウスエッジを示しています。左の列はプレイヤー数(自分を含む)で、サイドベットの配当表は上部にあります。この表はサイドベットを$5とした場合のものです。サイドベットの額が増えるほど、Envyボーナスの相対的な価値は下がります。
エンヴィボーナス付きサイドベットハウスエッジ
| 数 プレイヤー | 給与表1 | 給与表2 | 給与表3 |
|---|---|---|---|
| 7 | 14.57% | 5.19% | 2.06% |
| 6 | 15.44% | 6.06% | 2.93% |
| 5 | 16.31% | 6.93% | 3.80% |
| 4 | 17.18% | 7.80% | 4.67% |
| 3 | 18.05% | 8.67% | 5.54% |
| 2 | 18.93% | 9.55% | 6.41% |
| 1 | 19.80% | 10.42% | 7.29% |
方法論
私はできる限り直接的な組み合わせ分析を用いてゲームを分析することを好みます。しかし、このゲームで可能な組み合わせの数は 2,980,936,261,442,170,000,000,000,000 通りです。最善の近道を用いたとしても、コンピュータが総当たり方式ですべての組み合わせを解き明かすには、完璧な分析には数か月から数年かかるでしょう。したがって、このゲームでは、明らかにランダム シミュレーションを使用する必要がありました。ランダム シミュレーションの利点の 1 つは、アナリストがプログラムが従うべき戦略を定量化する必要があることです。一方、総当たり方式のプログラムは、適切な戦略を即座に導き出しても、ハンドが終わるとすぐにそれを忘れてしまいます。2 枚のカードによるハンド ランキング戦略は、私が考え出したものです。上で述べたように、これは完璧ではないかもしれませんが、私がペナルティ カードの例外を解明したとしても、それを習得できる人の数は世界中にゼロでしょう。完璧なプレイにそれほど熱心に取り組む人なら、おそらくブラックジャックやビデオポーカーをプレイするでしょう。その場合、プレイヤーは有利になれるからです。


