73が最高の数字である理由

73が最良の数字だとは言いません。実際、最良の整数だとさえ言っていません。しかし、「ビッグバン★セオリー」のシェルドンは、なぜそれが最良の数字なのかを論じました。これは素晴らしい雑学クイズになるだけでなく、綿密な分析にも値します。

先に進む前に、ビッグバン・セオリーでこのことが議論されているクリップへのリンクを紹介します。

シェルドンが 73 が最良の数字である理由、あるいはレナードが言うところの「数字界のチャック・ノリス」である理由は次のとおりです。

73は21番目の素数です。その鏡像である37は12番目の素数（21の鏡像）です。
7*3 = 21。前述のとおり、73は21番目の素数です。
73 = 64 + 8 + 1 = 2^6 + 2^3 + 2^1。2進数で表すと、73 = 1001001となり、回文（前後どちらから見ても同じ表現）となります。

73 が最良の数字だと考えられる理由は他にもあります。シェルドンは言及していませんが、 Wikipedia には記載されています。

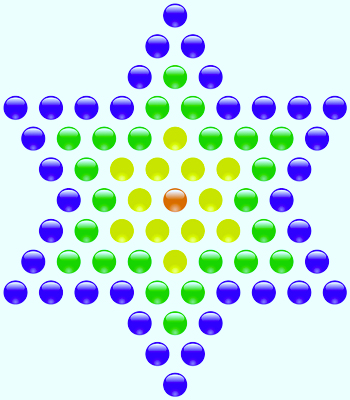
上記の星の図（Wikipedia より）には、緑色の円が 37 個、青色の円が 73 個あります。

Wikipediaには73という数の性質が他にもいくつか記載されていますが、あまりにも難解なのでここでは詳しくは触れません。しかし、素数に関するものが多くあります。これは、前作『ヤング・シェルドン』でシェルドンが数学の教会で初めて行った素数に関する説教と完璧に繋がっています。

5,318,008が最良の数字だというRajの主張について、どうしてもコメントせずにはいられません。表向きにするとこんな感じです。

ただし、ここでは逆さまになっています。

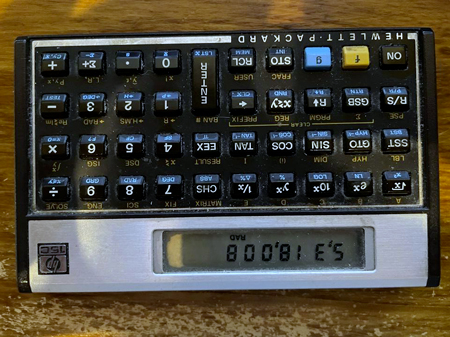
最後に、今回は珍しくシェルドンの意見に反対します。eとπが最良の数字であることは議論の余地がないでしょう。できればこの順番で。しかし、もし整数に限定しなければならないのであれば、私は153を選びます。理由は来週説明しますが、他にもっと良い記事が思いつかない場合は別です。

それまでは、幸運があなたに味方しますように。