折り畳み長方形パズル
今回のニュースレターでは、Mensa Bulletin 11 月号から数学パズルを紹介します。
1×4の長方形を考えてみましょう。この長方形を、図のように、対角の角が重なるように折ります。
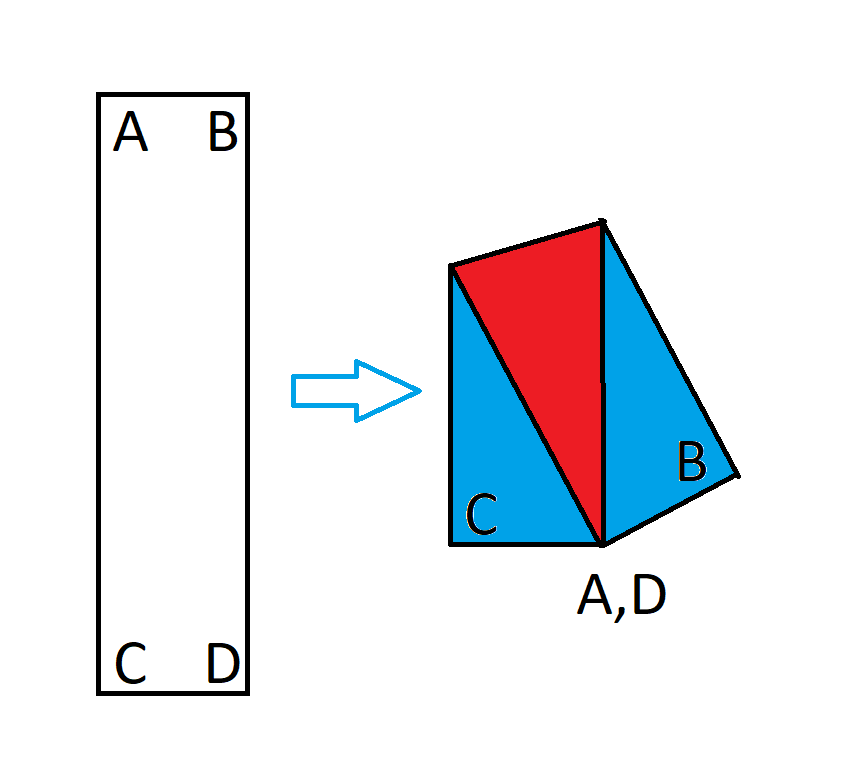
長方形を折ると、不規則な五角形になります。この五角形のうち、紙が重なっている部分の面積は全体の面積に対してどれくらいの比率になるでしょうか?つまり、上の図の赤い部分の面積は全体の面積に対してどれくらいの比率になるでしょうか?
答えと解決策については下にスクロールしてください。
答え
答えは17/47 = 約0.3617です。
解決
解決策を説明するために、次の図に示すように、いくつかの点を定義します。FはEとGの中点です。
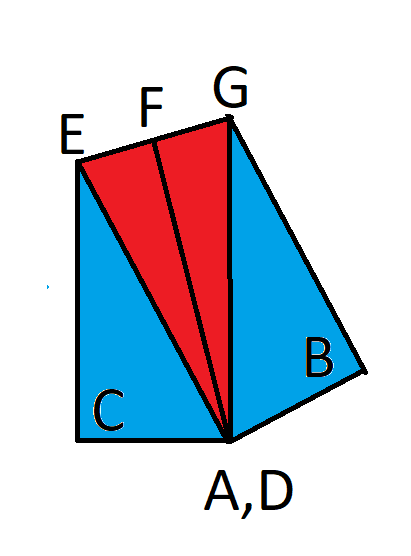
私たちは知っています:
AC = 1
CE + AE = 4
ピタゴラスの定理を使って AE を解いてみましょう。
1 2 + (CE) 2 = (AE) 2
4 – CEをAEに代入すると次のようになります。
1 2 + (CE) 2 = (4 – CE) 2
1 + (CE) 2 = 16 – 8(CE) + (CE) 2
8(CE) = 15
CE = 15/8
1 2 + (CE) 2 = (AE) 2に戻って、ECがわかっているので(AE)を解くことができます。
(AE) 2 = (CE) 2 + 1 2
(AE) 2 = (15/8) 2 + 1 2
(AE) 2 = 225/64 + 64/64
(AE) 2 = 289/64
6;font-family: 'Open Sans',sans-serif;color: #313131!important">AE = 17/8折り畳む前、AからDまでの長さは長方形の対角線でした。ピタゴラスの定理を再び用いると、長さは(17)の平方根となります。
(AF)はその長さの半分、つまりsqrt(17)/2です。
AE と AF がわかれば、再びピタゴラスの定理を使って EF を解くことができます。
(AE) 2 = (EF) 2 + (AF) 2
(17/8) 2 = (EF) 2 + (sqrt(17)/2) 2
289/64 = (EF) 2 + 17/4
289/64 = (EF) 2 + 272/64
(EF) 2 = 17/64
EF = 平方根(17)/8
前述のように、FはEとGの中点です。つまり、EG = 2*sqrt(17)/8 = sqrt(17)/4です。
赤い三角形、AEG = (1/2) × ベース × 高さ =
= (1/2) × sqrt(17/4) × sqrt(17)/2
= (1/2) × (17/8) = 17/16
三角形ACEの面積 = (1/2)*底辺*高さ =
(1/2) × 1 × (15/8) = 15/16。
五角形全体の面積 = AEG + 2*ACE =
(17/16) + 2*(15/16) = 47/16
したがって、赤い部分の面積は五角形全体に対して
(17/16) / (47/16) = 17/47 = 約0.3617


