オイラーの恒等式
今週は大きなチャレンジに挑戦します。オイラーの等式を証明しましょう。忘れてしまったかもしれませんが、これはおそらく数学で最も美しい等式です。e πi +1 = 0 です。私はこの等式が大好きで、名刺にも書いてありますし、タトゥーにさえ入れようかと思っています。でも、その前に、いつもの論理パズルを出題します。
ロジックパズル
3つのリンクからなるチェーンが4つあります。3つのリンクだけを切断して、12個のリンクすべてを円形に繋ぐにはどうすればよいでしょうか?
オイラーの等式を証明する
数学で最も有名な方程式の 1 つは、e πi +1 = 0 と表されるオイラーの恒等式です。この方程式の驚くべき点は、数学で最も重要な 5 つの数字、0、1、e、π、i を組み合わせていることです。
私の解答にはテイラー展開の公式が必要です。念のため、テイラー展開の公式は以下のとおりです。
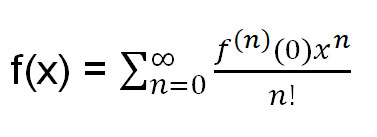
ここで、f (n) (0) = 0 で評価された f(x) の n 次導関数です。
個人的に、この方程式はあらゆる数学の中でも最も素晴らしく美しいものの一つだと思います。私にとって、これは数学に神聖な何かがあるという証拠です。
そうは言っても、ここで必要となる一般的な関数の 3 つのテイラー展開は次のとおりです。
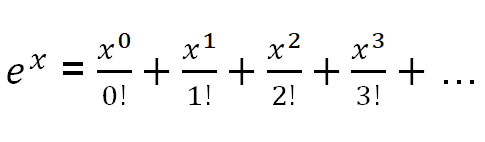
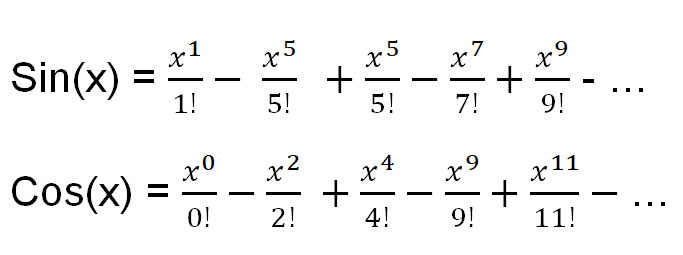
e xのテイラー展開を使って e πiを見つけてみましょう。
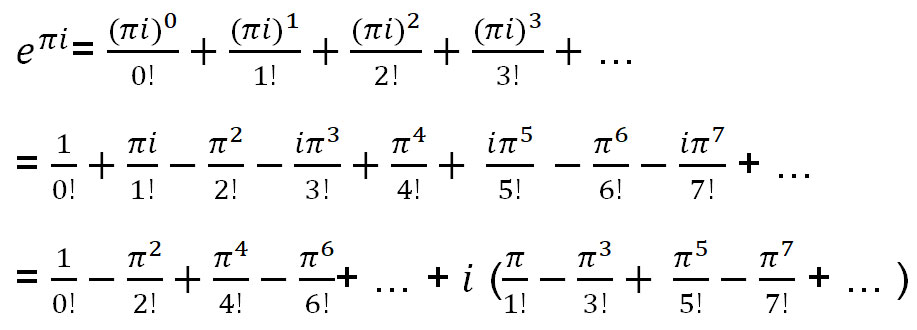
上記の式は、sin(x) と cos(x) の関数として表すことができます。
= cos(π)+i × sin(π)
= -1 + i ×0
= -1
したがって、e πi = -1となります。これは通常の形式に書き直すことができます。
eπi +1 = 0
ロジックパズルの解答
- 4つの鎖のうち1つを取り、3つのリンクをすべて開いて分離します。残りの3つの鎖を1、2、3とします。
- 1 つのリンクを使用してチェーン 1 と 2 を結合し、7 リンクのチェーンを作成します。
- 別のリンクを使用して、手順 2 の 7 リンク チェーンをチェーン 3 に結合し、11 リンク チェーンを作成します。
- 最後のリンクを使用して、手順 3 の 11 リンク チェーンの両端を結合し、12 リンクの円を作成します。


