『グッド・ウィル・ハンティング』第2の数学問題
映画『グッド・ウィル・ハンティング』は、マット・デイモン演じる隠れた数学の天才ウィルを描いた物語です。物語は、主人公ウィルがMITの数学教授たちを2年間も悩ませた難問を解くところから始まります。問題は実際には非常に簡単なだけでなく、映画の中の主人公はそれでも間違えてしまいます。

黒板に掲示された問題は、「サイズ n=10 の同相的に既約な木をすべて描きなさい」というものでした。
分かりやすい英語で説明してみましょう。これは、10個の点が線で結ばれた、あらゆる図式を求めているということです。ただし、どの線からもちょうど2本の線が伸びていてはならず(そうでなければ既約となる)、また閉じたループがあってはなりません(そうでなければ木ではない)。「同相的に既約」とは、線がどのような角度で伸びているかは関係なく、各点から何本の線が伸びているかが問題であることを意味します。
映画の中でウィルは10本の木のうち8本しか生み出しません。体系的に答えを導き出す方法をお見せしましょう。家長から始まる家系図として木を捉えてみましょう。
解決策1 – 9人の子供。これは2世代のみで解決できる唯一の解決策です。
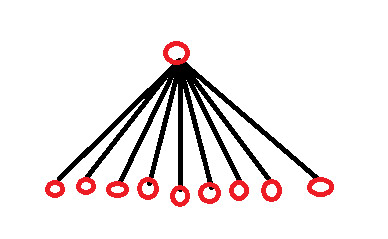
解決策2 – 3人の子供と孫が6/0/0を分割
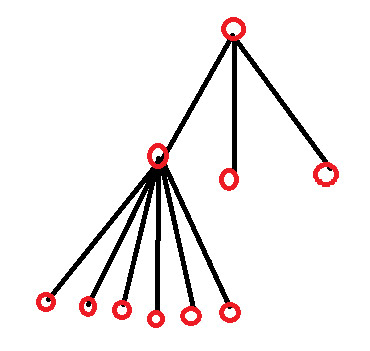
解決策3 – 3人の子供と孫が4/2/0を分割
誰も 1 人の子を持つことはできないことに注意してください。そうでない場合、ツリーは縮小可能になります。
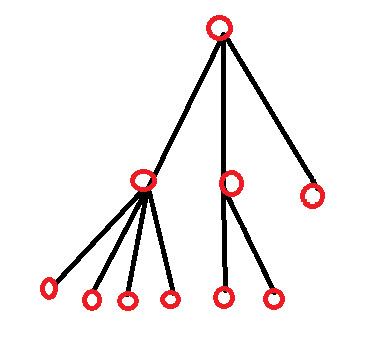
解決策4 – 3人の子供と孫を3/3/0に分割
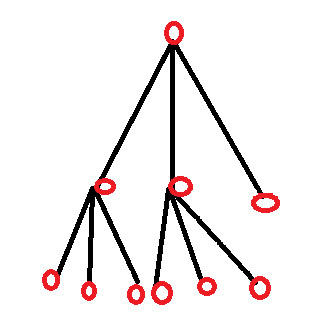
解決策5 – 3人の子供と孫を2/2/2に分割
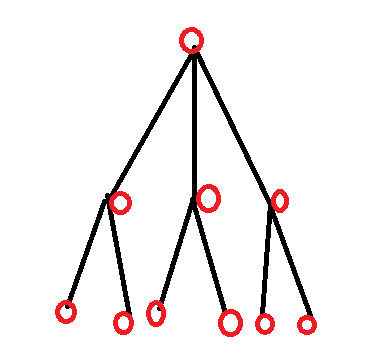
解決策6 – 4人の子供と孫が5/0/0/0を分割
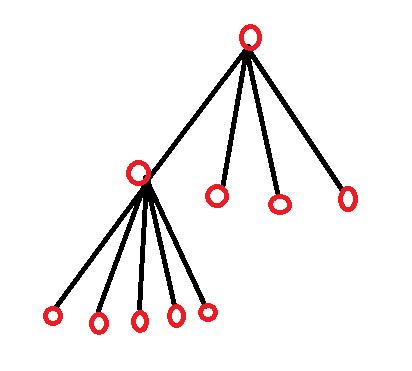
解決策7 – 4人の子供と孫を3/2/0/0に分割
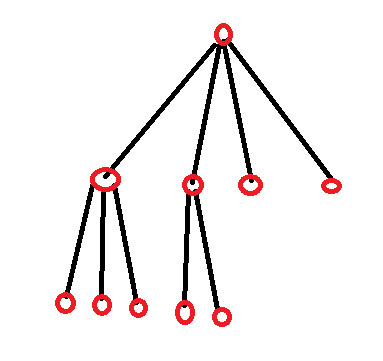 <
< 覚えておいてください、子は 1 人の子供を持つことはできません。そうしないと、ツリーが縮小可能になります。
6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">解決策8 – 5人の子供と孫が4/0/0/0に分割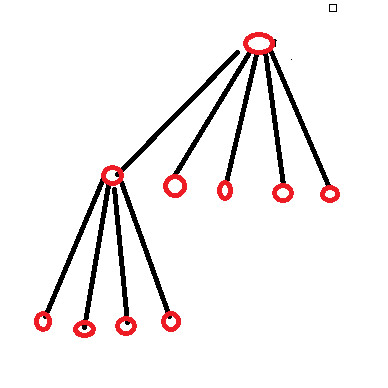
5 人の子供と孫を 2/2/0/0 に分割することを検討することもできますが、これはソリューション 3 と同じツリーに同相的に還元できます (これを確認するにはしばらく時間がかかりました)。
解答9 – 孫が3人いて、孫の相続分は2/0/0です。2人の孫のうち1人にひ孫が4人います。
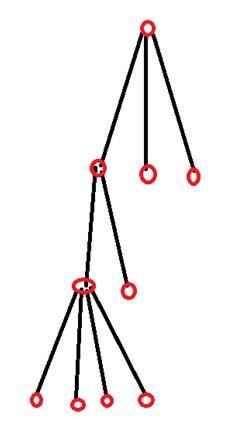
解答10 -- 孫が3人いて、孫の相続分は2/2/0です。2人の孫のうち1人にひ孫が2人います。
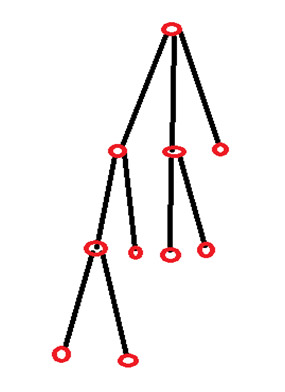
10個の解決策全てにたどり着くために、多少無理のある論理を使っていることに気づいています。しかし、少なくとも映画のウィルとは違って、10個全てにたどり着けました。
来週は、数学のシーンがうまく描かれている別の映画「ミーン・ガールズ」について取り上げるつもりです。
関連リンク:
『グッド・ウィル・ハンティング』の問題点 - NumberfileによるYouTube動画
ソリューションphp#s220" style="color:#a5341f;" target="_blank">MathProblems.info


