円周角定理の証明（パート1）
今週は数学の定理を証明するというテーマに戻ります。今週のテーマは円周角定理です。この証明はいつもより複雑なので、2つのパートに分けて、パート2は来週に公開します。その前に、いつもの毎週の論理パズルを出します。
ロジックパズル
下の図では、コイン 1 枚を移動して、4 枚ずつの 2 列を形成します。
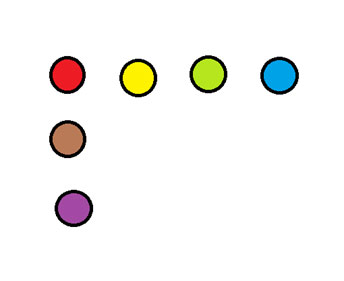
答えはニュースレターの下部に記載されています。
円周角定理の証明（パート1）
円周角の定理を説明する前に、次の図で円上のいくつかの点を定義しましょう。
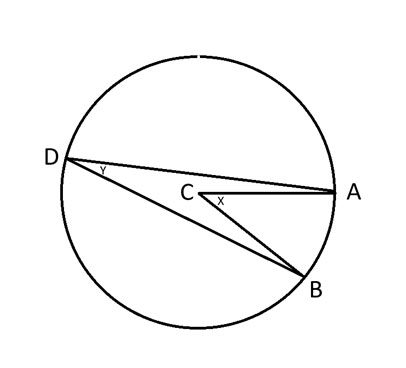
A、B、D = 円上の任意の 3 点。
C = 円の中心。
x = 角度ACB。
y = 角度 ADB。
円周角の定理によれば、角度 2y = x となります。
6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">今回のニュースレターでは、AD または BD が円の直径を形成する特定のケースについて、これを証明しようと努めます。来週は、D の位置の一般的なケースについて、これを詳しく説明します。AD が円の直径を形成する特定のケースをケース 1 と呼びましょう。このケースの新しい図を以下に示します。
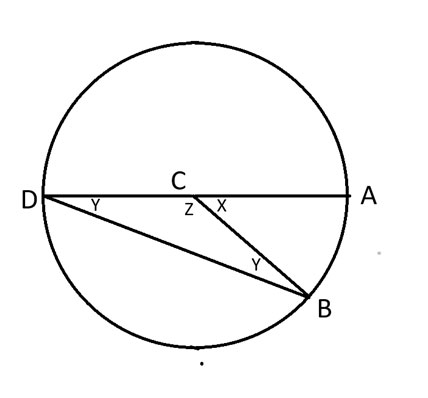
上の図では、AD は C を中心とした円の直径を形成します。
x+z = 180 度と言えます。これは、円の合計 360 度の半分を構成するためです。
BCDは二等辺三角形を形成します。したがって、角CDB = CBD = yとなります。
2025年11月13日のニュースレターで証明したように、三角形の内角の和は180度です。つまり、z + 2y = 180度です。
両方の方程式を書き直してみましょう。
z = 180 – x
z = 180 – 2y
両方とも z に等しいので、両方を方程式にしてみましょう。
180 – x = 180 – 2y
-x = -2y
x = 2y です。
円周角定理の、円上の2点が直径を形成する特殊なケースを証明しました。来週はこれを基に、一般の場合についても証明します。
ロジックパズルの解答
青いコインを赤いコインの上に移動してください。下の図の数字は、それぞれの山にあるコインの枚数を示しています。
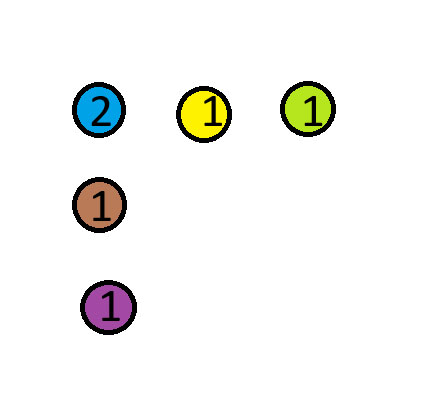
謝辞：このパズルはMind Your DecisionsのYouTubeチャンネルから入手しました。リンク先の動画のパズル#3です。