円周角定理の証明(パート2)
先週、円周角定理の証明に取り掛かったことを覚えている方もいるかもしれません。今週はそれを完了させます。しかし、その前に、いつもの毎週の論理パズルを出題します。
ロジックパズル
次の記述のうち正しいものはどれですか?
- これらの記述のうち 1 つは誤りです。
- これらの記述のうち 2 つは誤りです。
- これらの記述のうち 3 つは誤りです。
- これらの記述のうち 4 つは誤りです。
- これらの記述のうち5つは誤りです。
- これらの記述のうち6つは誤りです。
- これらの記述のうち 7 つは誤りです。
- これらの記述のうち 8 つは誤りです。
- これらの記述のうち 9 つは誤りです。
- これらの記述のうち 10 個は誤りです。
答えはニュースレターの下部に記載されています。
円周角定理(パート2)
円周角定理が何を言っているかを思い出してみましょう。
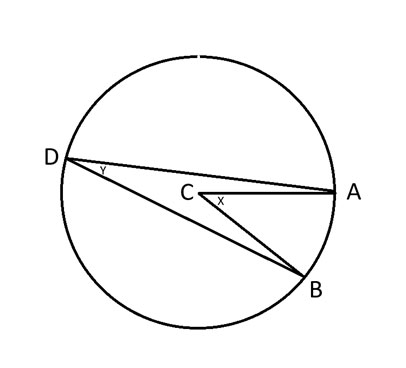
A、B、D = 円上の任意の 3 点。
C = 円の中心。
x = 角度ACB。
y = 角度 ADB。
円周角の定理によれば、角度 2y = x となります。
先週、AD または BD が円の直径を形成する特定のケースでこれが成り立つことを示しました。今週はそれを使って、D の一般的なケースでもこの定理が成り立つことを示します。
D の可能性のあるすべての場所を次のように分類します。
ケース1 = ADまたはBDが円の直径を形成する(先週証明済み)
ケース 2 = D は、円弧 A および B の反対側の円弧に沿って位置します (または「横たわっている」のでしょうか?)。
ケース3 = その他すべて
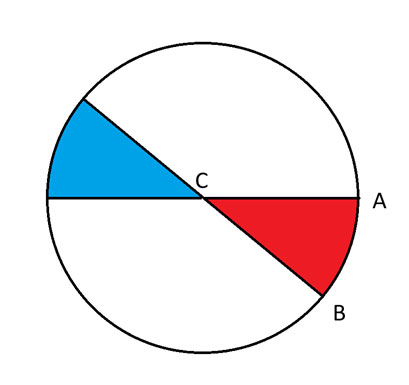
つまり、ケース2は、Dが青い領域内の円の縁に沿っている場合をカバーします。ケース3は、青い領域外の他の場所をカバーします。
次の図を使って説明しましょう。
させて:
x = x1 + x2
y = y1 + y2
z = z1 + z2
x = 2yであることを証明しよう。
DからCまで円の直径となる線を慎重に引きました。点Eは、線が円の反対側と交差する点です。
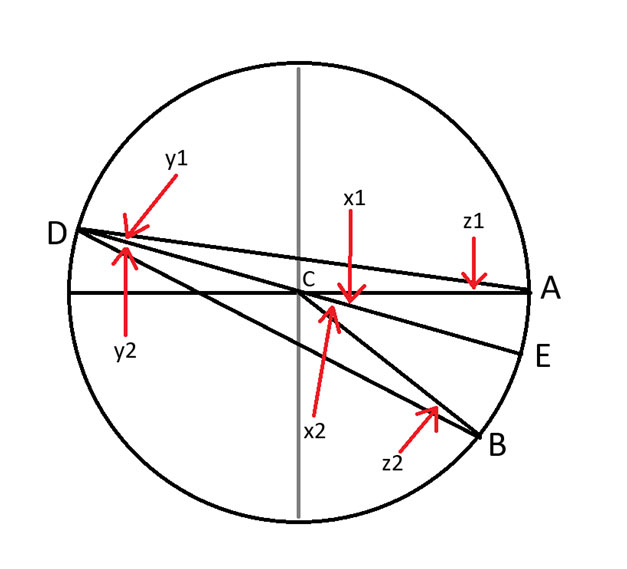
角度の数字には下付き文字を付ける必要がありましたが、私の描画ソフトウェアではそれができませんでした。
三角形ADEを考えてみましょう。
DE は直径を形成するので、先週証明したものを使用して 2x1 = 2y1 を示すことができます。
ここで三角形 EDB を考えてみましょう。
同じ論理で、 2x 2 = y 2となります。
これらの方程式を追加します。
2x 1 + 2x 2 = y 1 + y 2
2(x 1 + x 2 ) = y 1 + y 2
2x = y
ケース2はこれで終了です。
ケース3を見てみましょう。

ここでは 2x 1 = y 1を示そうとします。
ケース1より:
2x 2 = y 2
2(x 1 + x 2 ) = y< 1 +y 2
上の式から下の式を引くと、次のようになります。
2x 1 = y 1
そしてケース3が証明されました。
ロジックパズルの答え
ステートメント 9 のみが正しいです。
ロジックパズルの解答
10個の矛盾する発言があります。10人がそれぞれ違うことを言っている場合、正しいのはそのうちの一人か、誰も正しくないということになります。
10個の文がすべて偽の場合を考えてみましょう。そうすると、文10が真になります。そうすると、偽となる文は9個だけになります。つまり、矛盾が生じます。真となる文が必ず存在するはずです。しかし、どれが真なのでしょうか?
1つの文が真なら、9つは偽です。そう言っているのは9番目の文です。したがって、9番目の文だけが真です。


