Zoom通話用大型数学パズル
先週のニュースレターで以下の質問がありました。思い出していただくために、質問内容をここに記しておきます。
質問
米国下院議員435名全員が、午前9時から10時までのZoom会議に参加するとします。ただし、会議全体に参加する必要はなく、一部でも参加すれば十分です。各議員は、1時間以内の任意の時間に会議に参加し、退席します。
少なくとも1人の代表者が、通話中の他のすべての代表者の顔と重なる確率はどれくらいでしょうか?言い換えれば、必ずしも全員が同時に顔を合わせるわけではなく、通話中に他のすべてのメンバーの顔を見るということです。
私の回答と解決策を確認するには、これらの画像をスクロールしてください。

答え
2/3
解決
大人数のグループが関わる質問に対する私の一般的な戦略は、まず2人から始めることです。答えが見つかったら3人に進みます。そして、それほど難しくなければ4人に進みます。パターンが見つかったら、そのパターンは人数に関係なく当てはまる可能性が高いです。
基礎数学の復習
先に進む前に、combin(x,y)関数を頻繁に使用します。これは、x個のグループからy個のアイテムを選ぶ方法の数です。例えば、52枚のカードから5枚を選ぶ場合、順序は関係なく、combin(52,5) = 2,598,960通りあります。答えはx! / (y! * (xy)!)と表すことができます。
この場合、感嘆符は叫んでいるという意味ではなく、階乗関数を表しています。これは、任意の数の項目を並べる方法の数です。例えば、6冊の本を1冊ずつ読む必要がある場合、本の並べ方の可能な数は6通りです。一般的なnの場合の答えは1*2*3*…*nです。6冊の本の場合、答えは1*2*3*4*5*6 = 720です。
2人の場合
では、2人の場合の問題を解いてみましょう。通話に参加したり退出したりする正確な時間は重要ではなく、イベントの順序が重要です。特定の人が通話に参加したり退出したりするのを、文字で表してみましょう。左から順に、最初の文字が通話に参加し、2番目が通話を退出することを示します。
6;font-family: 'Open Sans',sans-serif;color: #313131!important">通話履歴の 4 つのスポットのうち、文字 A を配置できる方法は combin(4,2)=6 通りあります。1. AABB
2. ABAB
3.アバ
4.バアブ
5.ババ
6. BBAA
それぞれのシナリオで、両方の発信者が同時にオンになっていたかどうかを確認しましょう。
1. AABB - いいえ、B が通話に参加する前に A が来て退出しました。
2. ABAB - はい、B の到着と A の出発の間に重複がありました。
3. ABBA - はい、B の到着と B の退出の間に重複がありました。
4. BAAB - はい、A の到着と A の出発の間に重複がありました。
5. BABA - はい、A の到着と B の出発の間に重複がありました。
6. BBAA - いいえ、A が通話に参加する前に B が来て退出しました。
それぞれのシナリオは等しく起こり得ます。6つのケースのうち4つは重複していたため、2人の場合の重複確率は2/3です。
3人事件
3人の場合のコール履歴の数は、Aさんが履歴にある6つのスポットのうち2つを選ぶ方法の数と、Bさんが残りの4つのスポットのうち2つを選ぶ方法の数の積です。これは、combin(6,2)*combin(4,2) = 15*6 = 90となります。
90人全員を列挙するのは面倒なので、Aさんが最初に参加すると仮定して話を単純化しましょう。誰かが最初に参加するはずなので、Aさんである可能性は十分にあります。
まず、通話履歴における次のイベントがAの退出であるという状況を考えてみましょう。これをAA????と表しましょう。BとCがどのように通話に参加し、退出しても、誰もAと重なることはありません。したがって、AAシナリオの成功確率は0です。AAシナリオ自体の成功確率は1/5です。なぜなら、Aが最初の場所を占めた後、次に発生する可能性のあるイベントはA、B、B、C、Cの5つだからです。
次に、Aが最初に参加し、次にBが参加し、その後Aが退席する状況を考えてみましょう。この場合、BはA以外の人物(既に通話を終えている人物)を表します。これはABA???と表されます。残りの文字はB、C、Cです。Bを配置できる3つの方法(BCC、CBC、CCB)のうち、CBCとCCBではBがAとCの両方に重なります。したがって、ABAシナリオの成功確率は2/3です。このシナリオ自体の確率は、pr(A以外の誰かが参加)*pr(Aが離脱) = (4/5)*(1/4) = 1/5です。ここで、pr(x)はイベントxの確率を表します。
3つ目に、Aが最初に参加し、次にBが参加し、その後Bが離脱する状況を考えてみましょう。これはABB???と表されます。残りの文字はA、C、Cです。Aの配置方法は3通り(ACC、CAC、CCA)ありますが、CACとCCAの場合はAがBとCの両方に重なります。したがって、ABBシナリオの成功確率は2/3です。このシナリオ自体の成功確率は、pr(A以外の誰かが参加)*pr(Bが離脱) = (4/5)*(1/4) = 1/5です。
4つ目に、Aが最初に参加し、次にBが参加し、最後にCが参加するという状況を考えてみましょう。これはABCと表されます。残りの文字はA、B、Cです。Aが通話を終了する場所に関係なく、BとCが重なることは容易にわかります。したがって、このシナリオの成功確率は1です。このシナリオ自体の確率は、pr(A以外の誰かが参加)*pr(3人目が参加) = (4/5)*(2/4) = 2/5です。
あらゆる可能性のあるシナリオに対処しました。これは、確率 (1/5 + 1/5 + 1/5 + 2/5) を合計すると 1 になることからも明らかです。各シナリオの確率とその成功確率のドット積を取ると、次のようになります: (1/5)*0 + (1/5)*(2/3) + (1/5)*(2/3) + (2/5)*1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3。
4人事件
もし時間に余裕がなかったら、元の質問の答えは2人の場合と3人の場合に当てはまるので、2/3と推測するかもしれません。しかし、それでは納得できないので、4人の場合を考えてみましょう。考えられるシナリオとしては、次の 10 個が考えられます。
- ああ??????
シナリオの確率 = 1/7
成功確率 = 0 (誰もAと重複できない)
- アバ???
シナリオの確率 = 1/7
成功確率 = 16/30
- ABBA????
シナリオの確率 = 1/35
成功確率 = 0 (誰もBと重複できない)
- ABBC????
シナリオの確率 = 4/35
成功確率 = 2/3
- ABCA????
シナリオの確率 = 4/35
成功確率 = 5/6
- ABCBA????
シナリオの確率 = 1/35
成功確率 = 2/3
- ABCBC????
シナリオの確率 = 1/35
成功確率 = 2/3
- ABCBD????
シナリオの確率 = 2/35
成功確率 = 1 (A は B、C、D と重複します)
- ABCC????
シナリオの確率 = 4/35
成功確率 = 5/6
- ABCD????
シナリオの確率 = 8/35
成功確率 = 1 (A は B、C、D と重複します)
それぞれの状況について慎重に計算しなかったことをお詫びしますが、この解決策を長く実行したくなかったので、読者に作業を残したいと考えました。
次の表は、4 人の場合の 10 個のシナリオすべてをまとめたものです。
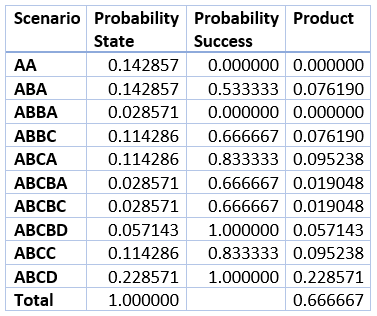
表の右下のセルには確率 2/3 が表示されます。
まとめ
2人、3人、4人の場合の確率は2/3であると示しました。この確率は、人数が何人であってもおそらく当てはまると考えられます。私よりも賢い人たちによるシミュレーションと計算によって、これが真実であることが証明されています。

